【机器学习基本理论】详解最大后验概率估计（MAP）的理解

【机器学习基本理论】详解最大后验概率估计（MAP）的理解

https://blog.csdn.net/weixin_42137700/article/details/81628065

最大似然估计（Maximum likelihood estimation, 简称MLE）和最大后验概率估计（Maximum a posteriori estimation, 简称MAP）是很常用的两种参数估计方法，如果不理解这两种方法的思路，很容易弄混它们。 下文将详细说明MLE和MAP的思路与区别。上篇讲解了MLE的相应知识。【机器学习基本理论】详解最大似然估计（MLE）、最大后验概率估计（MAP），以及贝叶斯公式的理解 下面讲解最大后验概率MAP的相关知识。 1最大后验概率估计 最大似然估计是求参数theta, 使似然函数p(x0|theta)最大。 最大后验概率估计则是想求theta使得p(x0|theta)p(theta)最大。

求得的theta不单单让似然函数大，theta自己出现的先验概率也得大。 （这有点像正则化里加惩罚项的思想，不过正则化里是利用加法，而MAP里是利用乘法）

MAP其实是在最大化p(theta|x0)=p(x0|theta)p(theta)/p(x0),不过因为x0是确定的（即投出的“反正正正正反正正正反”），p(x0)是一个已知值，所以去掉了分母p(x0) （假设“投10次硬币”是一次实验，实验做了1000次，“反正正正正反正正正反”出现了n次， 则p(x0)=n/1000总之，这是一个可以由数据集得到的值）。最大化p(theta|x0)的意义也很明确，x0已经出现了，要求theta取什么值使p(theta|x0)最大。顺带一提，p(theta|x0)即后验概率，这就是“最大后验概率估计”名字的由来。

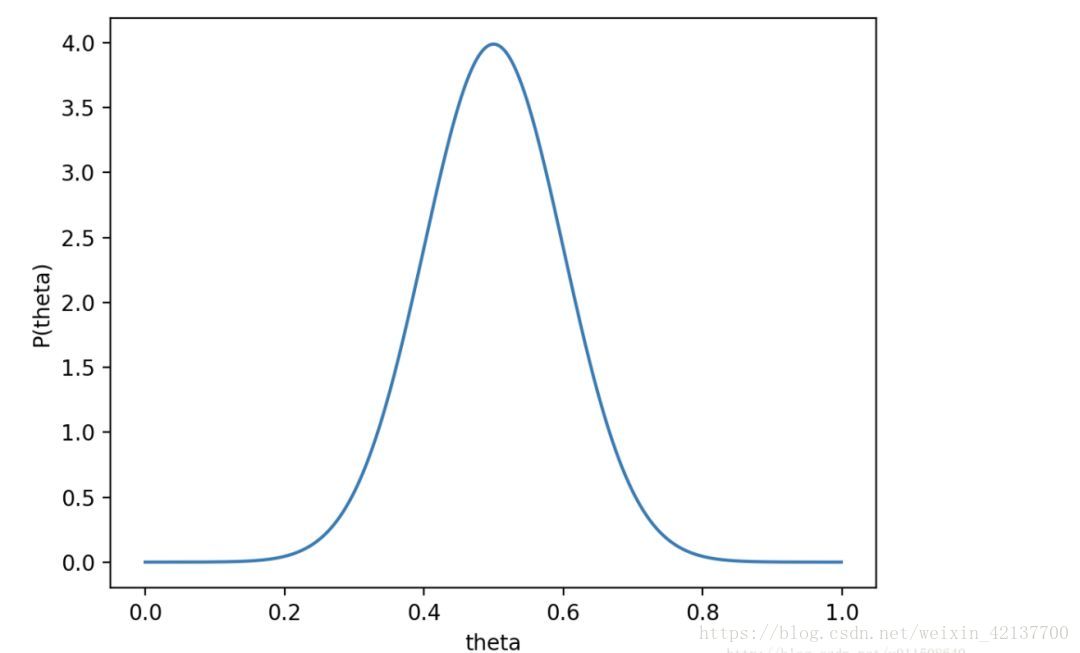
对于投硬币的例子来看，我们认为（”先验地知道“）theta取取0.5的概率很大，取其他值的概率小一些。我们用一个高斯分布来具体描述我们掌握的这个先验知识，例如假设p(theta)为均值0.5，方差0.1的高斯函数，如下图：

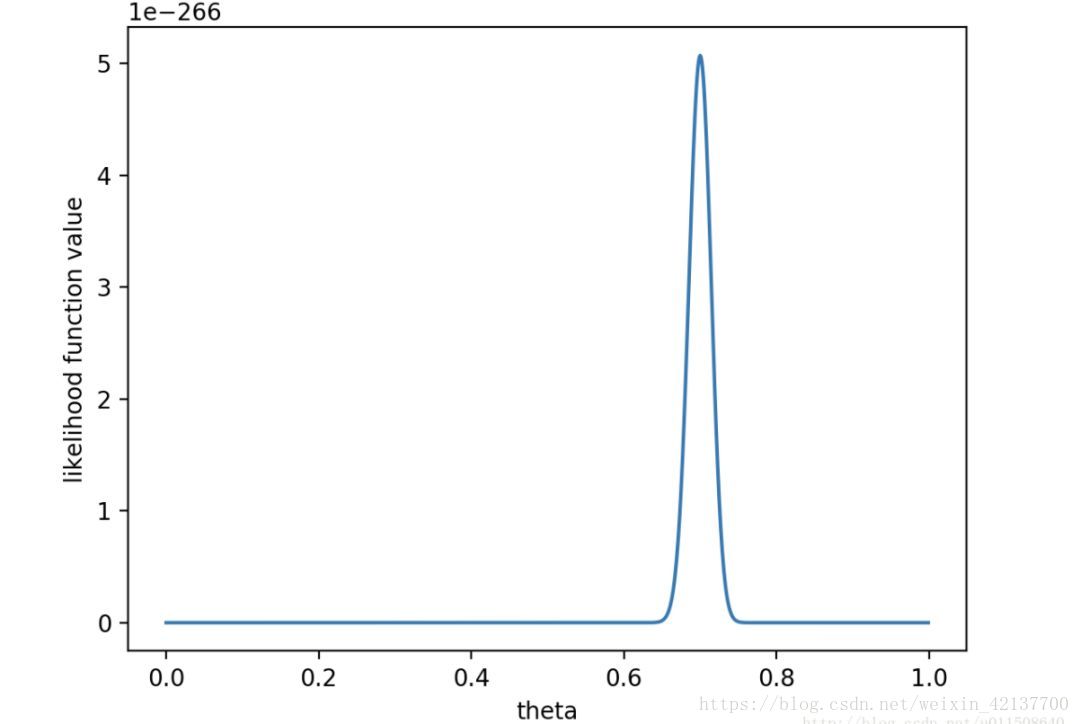
则p(x0|theta)p(theta)的函数图像为：

  注意，此时函数取最大值时，theta取值已向左偏移，不再是0.7。实际上，在theta=0.558时函数取得了最大值。即，用最大后验概率估计，得到theta=0.558。

最后，那要怎样才能说服一个贝叶斯派相信theta=0.7呢？ 你得多做点实验。。

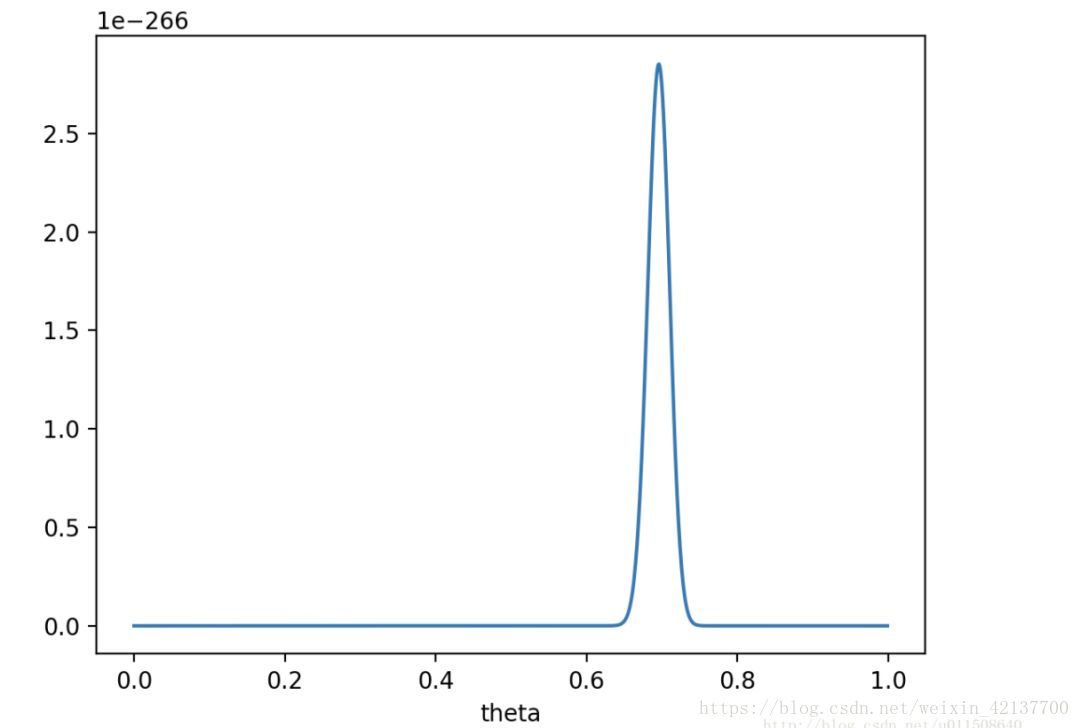
如果做了1000次实验，其中700次都是正面向上，这时似然函数为:  

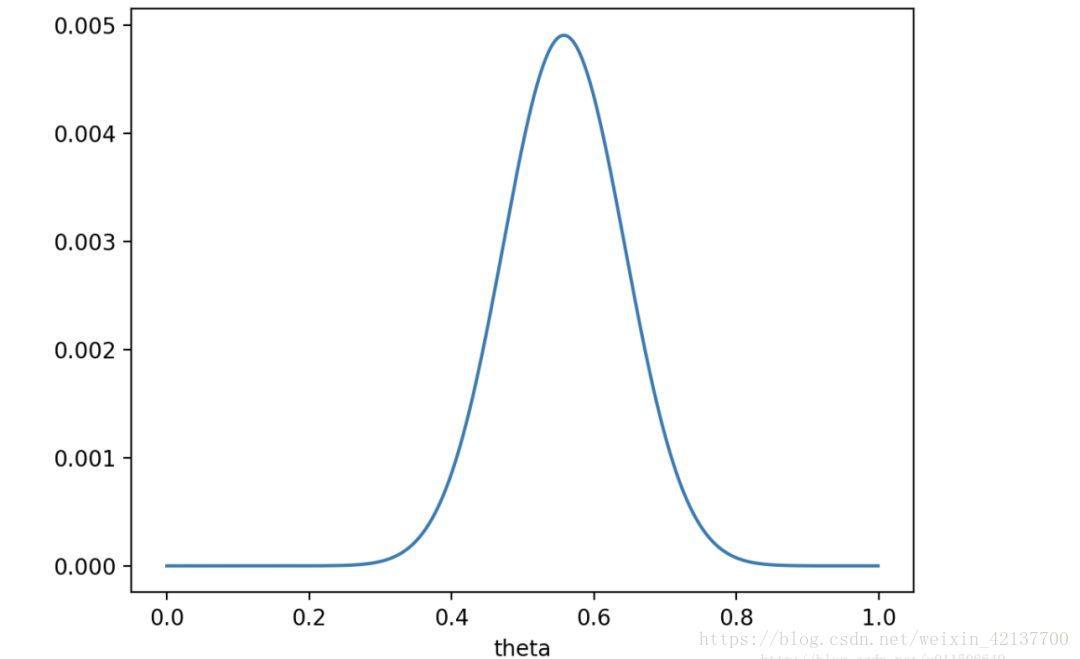
如果仍然假设p(theta)为均值0.5，方差0.1的高斯函数，则p(x0|theta)p(theta)的函数图像为：  

在theta=0.696，p(x0|theta)p(theta)取得最大值。

这样，就算一个考虑了先验概率的贝叶斯派，也不得不承认得把theta估计在0.7附近了。

PS. 要是遇上了顽固的贝叶斯派，认为p(theta=0.5)=1，那就没得玩了。。 无论怎么做实验，使用MAP估计出来都是theta=0.5。这也说明，一个合理的先验概率假设是很重要的。（通常，先验概率能从数据中直接分析得到）

2最大似然估计和最大后验概率估计的区别 相信读完上文，MLE和MAP的区别应该是很清楚的了。 MAP就是多个作为因子的先验概率p(theta)。 或者，也可以反过来，认为MLE是把先验概率p(theta)认为等于1，即认为theta为均匀分布，无论theta为何值，p(theta)均为1 文章地址：http://blog.csdn.net/u011508640/article/details/72815981