hdu 4165 dp

可以用卡特兰数做

以下分析转自：http://www.cnblogs.com/kevinACMer/p/3724640.html?utm_source=tuicool

这道题之前自己做的时候并没有反应过来是求卡特兰数，当时是按递推来想的。后来查了下HDU4165，结果一看大标题就说是卡特兰数，自己想了想， 还真是那么回事。主要还是对于卡特兰数用的不多，也就当时没立马反应过来了。下面介绍这道题我的思路，然后对卡特兰数再做一些补充。

本题题意：罐子里有N片相同的药片，开始的时候药片都是完整的一整片。然后一个每天从中任意取一片，如果该药片是完整的一整片，那么他会吃点半片， 然后将剩余半片扔回罐里，如果恰好是半片，那他直接吃掉拿出来的半片。显然2N天后，他吃完全部N片药片，总共有多少种不同的吃法过程。

我当时的思路顺序是这样的：发现对于一个状态，它的下一个状态会有两种可能（当然有些特殊情况是只有一种可能），那么对于这两种可能显然容易想到只 要递推下去就行了。然后再考虑，这两种可能无非就是下个状态我可能吃完整的药片，也可能吃只有半片的药片。所以递推显然设计两个参数，完整药片的个数和只 有半片药片的个数。于是开了个二维数组dp[i][j],表示当罐子里有i片完整的药片和j片只有一半的药片时距离吃完总共有多少种不同的吃法。

然后递推过程应该比较容易就出来了：dp[i][j]=dp[i-1][j+1]+dp[i][j-1],递推式说明：对于当前dp[i][j]这 个状态来说，它接下来会出现两个分叉，一种可能，接下来拿出的是一枚完整的药片，然后吃一半，扔回一半，于是变成了dp[i-1][j+1]这个状态,还 一种可能就是正好拿出来的是只有半片的药片，于是变成了dp[i][j-1]这个状态。然后由于DP定义的是方案数，显然这两个之后的状态加起来的方案数 就是之前那个状态的方案数了。

当然，接下来就是给这个二维dp赋初始值了，显然dp[1][0]=1,然后发现其实dp[1][i]=i+1（可以这样理解：当罐子里只有i片半 状的药片和1片完整药片时，对于求方案数，其实主要就是看那个完整的药片在第几天吃，总共i+1天，那么显然就是C（i+1）（1）种方案数）。然后 dp[i][j]中的i相当于就从2开始递推了。对于j，当j为0时，它对应的下一个状态其实只有一种可能，就是dp[i][0]=dp[i-1] [1]，于是j就从1开始递推了。具体代码如下：

2015-05-11

 #include<cstdio>
 #include<iostream>
 #include<algorithm>
 #include<cstring>
 #include<cmath>
 #include<queue>
 #include<map>
 using namespace std;
 #define MOD 1000000007
 const int INF=0x3f3f3f3f;
 const double eps=1e-;
 typedef long long ll;
 #define cl(a) memset(a,0,sizeof(a))
 #define ts printf("*****\n");
 const int MAXN=;
 ll dp[MAXN][MAXN];
 int n,m,tt;
 void init()
 {
     for(int i=;i<MAXN;i++)    dp[][i]=i+;
     for(int i=;i<MAXN;i++)
     {
         dp[i][]=dp[i-][];
         for(int j=;j<MAXN;j++)
         {
             dp[i][j]=dp[i-][j+]+dp[i][j-];
         }
     }
 }
 int main()
 {
     int i,j,k;
     #ifndef ONLINE_JUDGE
     freopen("1.in","r",stdin);
     #endif
     int n;
     init();
     while(scanf("%d",&n)!=EOF)
     {
         if(n==)break;
         printf("%I64d\n",dp[n][]);
     }
     return ;
 }

本题思路就是这样，比较简单的递推。但之后看到一些题解，对于本题，其实就是求卡特兰数。
我们这样来思考：本题的题意转化一下可以这样理解，有N个红球，N个白球，问这2N个小球的排列数，且从第一个球到后面任意个球中红球的个数必须不小于白球的个数（理解为白球是红球产生的，一个红球产生一个白球）。那么这个就变成了卡特兰数的一个典型应用了。

卡特兰数：

令h(0)=1,h(1)＝1,catalan数满足递归式：

h(n)= h(0)*h(n-1) + h(1)*h(n-2) + + h(n-1)h(0) (其中n>=2) 　　

该递推关系的解为： 　　h(n)=C(2n,n)/(n +1) (n=1,2,3,)

另类递归式：  h(n)=((4*n-2)/(n+1))*h(n-1);

组合数学中有非常多.的组合结构可以用卡塔兰数来计数。以下用C_n=3和C_n=4举若干例：

• C_n表示长度2n的dyck word的个数。Dyck word是一个有n个X和n个Y组成的字串，且所有的部分字串皆满足X的个数大于等于Y的个数。以下为长度为6的dyck words:

XXXYYY XYXXYY XYXYXY XXYYXY XXYXYY

• 将上例的X换成左括号，Y换成右括号，C_n表示所有包含n组括号的合法运算式的个数:

((())) ()(()) ()()() (())() (()())

• C_n表示有n+1个叶子的二叉树的个数。

• C_n表示所有不同构的含n个分枝结点的满二叉树的个数。（一个有根二叉树是满的当且仅当每个结点都有两个子树或没有子树。）

• 证明：

  令1表示进栈，0表示出栈，则可转化为求一个2n位、含n个1、n个0的二进制数，满足从左往右扫描到任意一位时，经过的0数不多于1数。显然含n个1、n个0的2n位二进制数共有个，下面考虑不满足要求的数目.

  考虑一个含n个1、n个0的2n位二进制数，扫描到第2m+1位上时有m+1个0和m个1（容易证明一定存在这样的情况），则后面的0-1排列中必有n-m个1和n-m-1个0。将2m+2及其以后的部分0变成1、1变成0，则对应一个n+1个0和n-1个1的二进制数。反之亦然（相似的思路证明两者一一对应）。

  从而。证毕。

• • C_n表示所有在n×n格点中不越过对角线的单调路径的个数。一个单调路径从格点左下角出发，在格点右上角结束，每一步均为向上或向右。计算这种路径的个数等价于计算Dyck word的个数： X代表“向右”，Y代表“向上”。下图为n= 4的情况：
  • 
  • C_n表示通过连结顶点而将n + 2边的凸多边形分成三角形的方法个数。下图中为n= 4的情况：

  

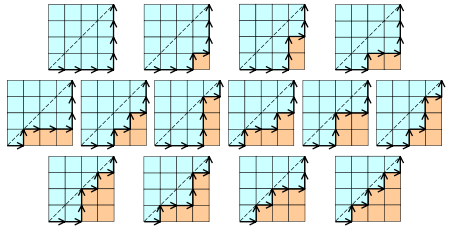
  • C_n表示对{1, ...,n}依序进出栈的置换个数。一个置换w是依序进出栈的当S(w) = (1, ...,n), 其中S(w)递归定义如下：令w=unv，其中n为w的最大元素，u和v为更短的数列；再令S(w) =S(u)S(v)n，其中S为所有含一个元素的数列的单位元。
  • C_n表示集合{1, ...,n}的不交叉划分的个数. 那么,C_n永远不大于第n项贝尔数.C_n也表示集合{1, ..., 2n}的不交叉划分的个数，其中每个段落的长度为2。综合这两个结论，可以用数学归纳法证明 that all of thefreecumulants of degree more than 2 of theWigner semicircle laware zero. This law is important infree probabilitytheory and the theory ofrandom matrices.
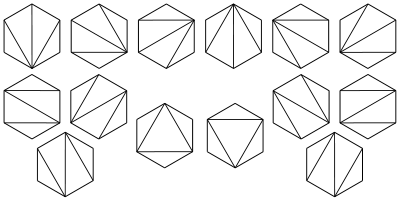
  • C_n表示用n个长方形填充一个高度为n的阶梯状图形的方法个数。下图为n = 4的情况: