汇编学习：float与double速度问题

X86处理器包含两种类型的浮点数寄存器。第一种使用8个浮点寄存器组成浮点寄存器栈，另一种为向量寄存器(XMM,YMM)，它们对于单双精度的处理是不同的。本文将讨论两种模式下的浮点数计算速度问题。

一、当我们编译32位程序时,使用的是x87指令集，即使用浮点寄存器堆栈进行浮点计算。此种情况下，单精度与双精度的处理是统一的，故计算速度上没有差异。我们可以做如下验证：

float a,b,c;
c=a*b;
汇编：
fld         dword ptr [a]  //将a加载到浮点栈顶,即ST(0)=a;
fmul        dword ptr [b]  //将栈顶元素与b相乘，结果仍存于栈顶,即ST(0)=ST(0)*b
fstp        dword ptr [c]  //将栈顶元素弹出并保存于c,即c=ST(0),POP();

double  a,b,c;
c=a*b;
汇编：
fld         qword ptr [a]
fmul        qword ptr [b]
fstp        qword ptr [c]  

可以发现，上述两段代码的汇编代码完全相同.

因此，此种情况下，float与double的计算速度没有差异。在精度满足要求的情况下，可以使用float以便加载更多数据到cache，以提高cache命中率。

二、当编译64 位程序或打开MMX ,SSE,AVX指令集优化时，则使用向量寄存器。在此情况下,float与double的处理使用的是不同汇编指令，关于二者的计算速度，可以参考《Optimizing software in C++》中的一段话：

Single precision division, square root and mathematical functions are calculated faster than double precision when the XMM registers are used, while the speed of addition, subtraction, multiplication, etc. is still the same regardless of precision on most processors (when vector operations are not used).

意思是当使用XMM寄存器时，单精度浮点的除法、开根及一些数学函数的执行要比双精度快，但加法，减法、乘法的计算速度二者没有差异（在没有使用向量操作时）。

此处的向量操作指SIMD，即单指令多数据流。基本思想是将若干个数据加载到一个寄存器内部，一条指令可以同时处理多个数据，一个XMM(128位)可同时装载4个double或8个float,因此在使用SIMD时，一次处理的float数据量为double的两倍。

为了验证64位程序中的float和double的速度差异，下面给出测试程序：

float SqrtfloatV1(float *A,const int len)
{
    float fSum=;
    for (int i=;i<len;i++)
    {
        fSum+=sqrt(A[i]);
    }
    return fSum;
}
 
double SqrtdoubleV1(double *A,const int len)
{
    double dSum=;
    for(int i=;i<len;i++)
    {
        dSum+=sqrt(A[i]);
    }
    return dSum;
}

测试结果：

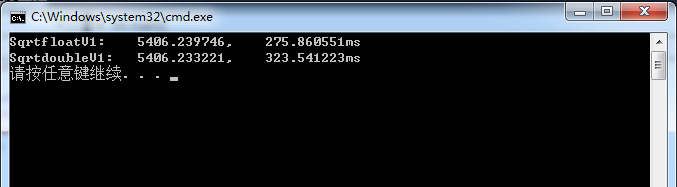
注意事项：

一、浮点数到整数（直接截断）的转换是很低效的，使用浮点堆栈（32位程序）时需要调用函数_ftol2_sse.

double  a,b;
int c;
c=a*b;
汇编：
fld         qword ptr [a]
fmul        qword ptr [b]
call        @ILT+(__ftol2_sse) (0EC10CDh) //调用函数_ftol2_sse实现浮点数到整数的转换
mov         dword ptr [c],eax  

使用XMM寄存器（64位程序）需要指令cvttsd2si：

double  a,b;
int c;
c=a*b;
汇编：
movsd       xmm0,mmword ptr [a]
mulsd       xmm0,mmword ptr [b]
cvttsd2si   eax,xmm0  //cvttsd2si指令实现
mov         dword ptr [c],eax  

下面是测试程序，对一个浮点数组求和:

float AddfloatV1(float *A,const int len)
{
    int iSum=;
    for (int i=;i<len;i++)
    {
        iSum+=A[i];//转成整数再求和
    }
    return (float)iSum;
}
 
float AddfloatV2(float *A,const int len)
{
    float fSum=;
    for (int i=;i<len;i++)
    {
        fSum+=A[i];
    }
    return fSum;
}

对于32位程序，测试结果如下：

于64位程序，测试结果如下：

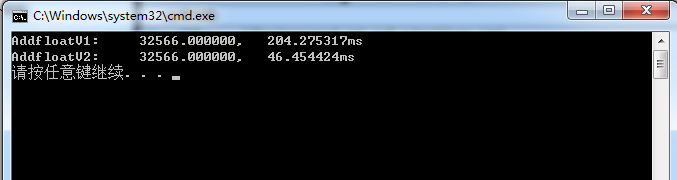
可以看出不管是32位还是64位程序，将浮点数转为整数再求和都会造成效率的大大降低。

关于浮点转整数的优化的讨论，可以参考一篇博文[1].

二、使用XMM寄存器（即当编译64位程序或打开SSE2指令集时），应避免float与double混用，因为编译器需要在计算过程中进行转换。如下：

(1)float与double混用(默认的浮点常量为double)

float a,b;
a=b*1.2;
汇编
movd        xmm0,dword ptr [b]
cvtps2pd    xmm0,xmm0
mulsd       xmm0,mmword ptr [__real@3ff3333333333333 (13F646790h)]
cvtsd2ss    xmm0,xmm0
movss       dword ptr [a],xmm0  

（2）纯float

float a,b;
a=b*1.2f;
汇编
movss       xmm0,dword ptr [b]
mulss       xmm0,dword ptr [__real@3f99999a (13F84678Ch)]
movss       dword ptr [a],xmm0  

可以看到，（1）中多了两个指令，即cvtps2pd,cvtsd2ss,它们分别实现float转double,double转float。

下面是一段测试程序:

float MulfloatV1(float *A,const int len)
{
    float fSum=;
    for (int i=;i<len;i++)
    {
        fSum+=A[i]*1.2f;
    }
    return fSum;
}
 
float MulfloatV2(float *A,const int len)
{
    float fSum=;
    for (int i=;i<len;i++)
    {
        fSum+=A[i]*1.2;//默认的浮点常数是double
    }
    return fSum;
}

测试结果:

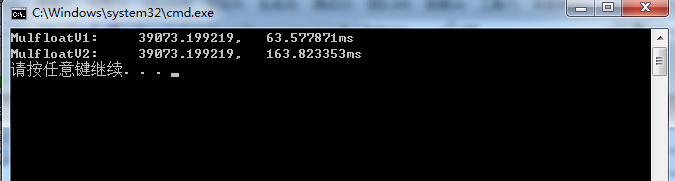
完整的测试程序：

#include <stdio.h>
#include <time.h>
#include <stdlib.h>
#include <math.h>
#include "Timing.h"
const int BUFSIZE =;
float buf[BUFSIZE];
double buf2[BUFSIZE];
 
//测试64位下float与double的速度差
float SqrtfloatV1(float *A,const int len);
double SqrtdoubleV1(double *A,const int len);
 
//测试浮点数转整数的速度
float AddfloatV1(float *A,const int len);
float AddfloatV2(float *A,const int len);
 
//测试64位下float与double混用速度
float MulfloatV2(float *A,const int len);
float MulfloatV1(float *A,const int len);
 
int main()
{
    const int testloop=;
    double interval;
    srand( (unsigned)time( NULL ) );
    for (int i = ; i < BUFSIZE; i++)
    {    
 
        buf[i] = (float)(rand() & 0x3f);
        buf2[i]= (double)(buf[i]);
    }
    //*****************************************************************//
    //测试64位下float与double的速度差(32位无明显差异)
    volatile float result1=;
    startTiming();
    for(unsigned int i=;i<testloop;i++)
    {
        result1=SqrtfloatV1(buf,BUFSIZE);
    }
    interval=stopTiming();
    printf("SqrtfloatV1:\t%f,\t%lfms\n",result1,interval);
 
    volatile double result2=;
    startTiming();
    for(unsigned int i=;i<testloop;i++)
    {
        result2=SqrtdoubleV1(buf2,BUFSIZE);
    }
    interval=stopTiming();
    printf("SqrtdoubleV1:\t%lf,\t%lfms\n",result2,interval);
    //*****************************************************************//
 
    //*****************************************************************//
    //测试浮点数转整数的速度(32为与64位均有明显差异)
    volatile float result3=;
    startTiming();
    for(unsigned int i=;i<testloop;i++)
    {
        result3=AddfloatV1(buf,BUFSIZE);
    }
    interval=stopTiming();
    printf("AddfloatV1:\t%f,\t%lfms\n",result3,interval);
 
    volatile float result4=;
    startTiming();
    for(unsigned int i=;i<testloop;i++)
    {
        result4=AddfloatV2(buf,BUFSIZE);
    }
    interval=stopTiming();
    printf("AddfloatV2:\t%f,\t%lfms\n",result4,interval);
    //*****************************************************************//
 
    //*****************************************************************//
    //测试64位下float与double混用速度(32位无差异,因统一处理)
    volatile float result5=;
    startTiming();
    for(unsigned int i=;i<testloop;i++)
    {
        result5=MulfloatV1(buf,BUFSIZE);
    }
    interval=stopTiming();
    printf("MulfloatV1:\t%f,\t%lfms\n",result5,interval);
 
    volatile float result6=;
    startTiming();
    for(unsigned int i=;i<testloop;i++)
    {
        result6=MulfloatV2(buf,BUFSIZE);
    }
    interval=stopTiming();
    printf("MulfloatV2:\t%f,\t%lfms\n",result6,interval);
    //*****************************************************************//
    return ;
}
 
float SqrtfloatV1(float *A,const int len)
{
    float fSum=;
    for (int i=;i<len;i++)
    {
        fSum+=sqrt(A[i]);
    }
    return fSum;
}
 
double SqrtdoubleV1(double *A,const int len)
{
    double dSum=;
    for(int i=;i<len;i++)
    {
        dSum+=sqrt(A[i]);
    }
    return dSum;
}
 
float AddfloatV1(float *A,const int len)
{
    int iSum=;
    for (int i=;i<len;i++)
    {
        iSum+=A[i];//转成整数再求和
    }
    return (float)iSum;
}
 
float AddfloatV2(float *A,const int len)
{
    float fSum=;
    for (int i=;i<len;i++)
    {
        fSum+=A[i];
    }
    return fSum;
}
 
float MulfloatV1(float *A,const int len)
{
    float fSum=;
    for (int i=;i<len;i++)
    {
        fSum+=A[i]*1.2f;
    }
    return fSum;
}
 
float MulfloatV2(float *A,const int len)
{
    float fSum=;
    for (int i=;i<len;i++)
    {
        fSum+=A[i]*1.2;//默认的浮点常数是double
    }
    return fSum;
}

参考：

[1]http://blog.csdn.net/housisong/article/details/1616026