线段树和zkw线段树

作者作为一个蒟蒻，也是最近才自学了线段树，不对的地方欢迎大佬们评论，但是不要喷谢谢

好啦，我们就开始说说线段树吧

线段树是个支持区间操作和查询的东东，平时的话还是蛮实用的

下面以最基本的区间加以及查询区间和为例

线段树顾名思义就是棵树嘛，叶子节点是每个基本点，它们所对应的父亲就是它们的和，具体如下图

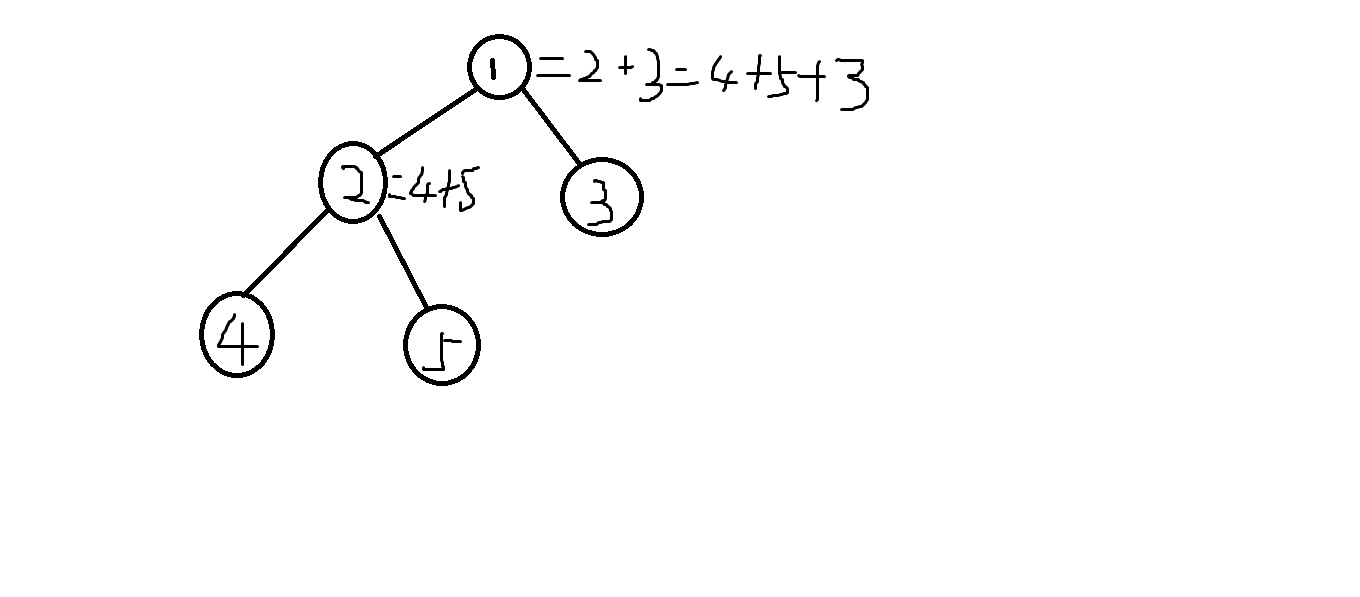
但是对于这样的线段树来说，操作所需的时间是远达不到我们的要求的（会被t），因为我们会进行一些不必要的操作，就像如果没有查询到某个点，那么就没有必要去修改这个点的值，为此，我们会引入一个懒标记，记录每个基本点需要被加上的值（称为add），那么树上任意一个点需要增加的值=该点对应的区间长度*add

那么总的来说，线段树的基本操作我个人认为可以分成3个，建树、修改和查询，当然如果继续细分也是口以（可以）的，就比如说还可以分出 区间和的向上传递（父亲节点等于子节点的和）和懒标记的向下传递（子节点的懒标记=原来的懒标记+父节点的懒标记）

所以接下来我们就来看看建树、修改和查询这3部分的具体代码吧（深呼吸）

首先是建树（build）

#define ls 2*rt,l,(l+r)/2                //left son
#define rs 2*rt+1,(l+r)/2+1,r      //right son
#define ll long long
void build(ll rt,ll l,ll r)//rt是当前点，l和r代表l到r区间的和
{
    if(r==l)
//也就是说，我们找到了一个叶子节点，自己到自己的和 就是自己嘛
    {
        scanf("%lld",&su[rt]);//那我们就输入这个节点的值
    }
    else//否则就去看看当前点的左右儿子
    {
        build(ls);//看左儿子
        build(rs);//看右儿子
        //当rt的左右儿子都准备好了，我们就可以求出rt的值了
        su[rt]=su[*rt]+su[*rt+];
    }
    return;
} //一层一层的求，我们就可以建好一个初步的树啦

然后是修改（change）

#define ls 2*rt,l,(l+r)/2          //左右儿子，和之前一样
#define rs 2*rt+1,(l+r)/2+1,r
#define ll long long
void change(ll rt,ll l,ll r,ll L,ll R,ll add)
//当前点，当前区间的左右端点，需要修改的区间的左右端点，需要给每个基本点加上的值
{
    if(l>=L&&r<=R)//如果说当前区间是需要修改区间的子集
    {
        su[rt]+=add*(r-l+);
        //那么就修改当前点，注意乘上当前区间长度
        o[rt]+=add;
        //记得修改懒标记
        return;//别忘了返回！
    }
    if(o[rt]!=)
    //如果说我们恰好经过了一个被打上懒标记的点，那不如就顺手把它的懒标记下传好了
    {
        //修改左右儿子的值
        su[rt*]+=o[rt]*((r+l)/-l+);// （r+l）/2是区间中点
        su[rt*+]+=o[rt]*(r-(r+l)/);//实际应乘以(r-（(r+l)/2+1）+1)但+1-1抵消了
        o[rt*]+=o[rt];
        o[rt*+]+=o[rt];
        //下传懒标记注意是加上父节点的懒标记不是等于
        o[rt]=;//清除懒标记
    }
    if(L<=(l+r)/)
    //二分思想，如果需要修改的区间左端点在当前区间中点的左边，即当前区间中点左侧有需要修改的点的话
    {
        change(ls,L,R,add);//那就去修改啊
    }
    if(R>(l+r)/)//同理
    {
        change(rs,L,R,add);
    }
    su[rt]=su[*rt]+su[*rt+];//橘氏春秋有云（什么鬼）：有下就有上，改完记得上传
    return;
}

呼啊，已经完成2/3了，坚持就是胜利！↖(^ω^)↗

查询（find）

void find(ll rt,ll l,ll r,ll L,ll R)
//当前点，当前区间左右端点，需要查询的区间左右端点
{
    if(l>=L&&r<=R)//如果当前区间是查询区间的子集
    {
        ans[c]+=su[rt];//答案就加上当前点的值
    }
    else//不然就找找它应该在那个区间里面
    {
        if(o[rt]!=)//顺便下传rt的懒标记
        {
            su[rt*]+=o[rt]*((r+l)/-l+);
            su[rt*+]+=o[rt]*(r-(r+l)/);
            o[rt*]+=o[rt];
            o[rt*+]+=o[rt];
            o[rt]=;
        }
        if(L<=(l+r)/)//二分思想，如果左边有点
        {
            find(ls,L,R);//那就找找左边
        }
        if(R>(l+r)/)//如果右边有点
        {
            find(rs,L,R);//那就找找右边
        }
        su[rt]=su[*rt]+su[*rt+];//还是那句老话，橘氏春秋有云：有下就有上
    }
    return;//看到return我就开心↖(^ω^)↗
}

哇吼，结束了才怪，接下来是总代码！

//线段树要写成lazy[i]+=lazy[祖先]的形式
//温馨提示，炒鸡重要，我这个蒟蒻就被坑了嘤嘤嘤
#include<iostream>
#include<cstdio>
#define ls 2*rt,l,(l+r)/2
#define rs 2*rt+1,(l+r)/2+1,r
#define ll long long
using namespace std;
int n,m,a,c;
ll su[],x,y,k,ans[],o[];//数组开4倍
void build(ll rt,ll l,ll r)
{
    if(r==l)
    {
        scanf("%lld",&su[rt]);
    }
    else
    {
        build(ls);
        build(rs);
        su[rt]=su[*rt]+su[*rt+];
    }
    return;
}
void change(ll rt,ll l,ll r,ll L,ll R,ll add)
{
    if(l>=L&&r<=R)
    {
        su[rt]+=add*(r-l+);
        o[rt]+=add;
        return;
    }
    if(o[rt]!=)
    {
        su[rt*]+=o[rt]*((r+l)/-l+);
        su[rt*+]+=o[rt]*(r-(r+l)/);
        o[rt*]+=o[rt];
        o[rt*+]+=o[rt];
        o[rt]=;
    }
    if(L<=(l+r)/)
    {
        change(ls,L,R,add);
    }
    if(R>(l+r)/)
    {
        change(rs,L,R,add);
    }
    su[rt]=su[*rt]+su[*rt+];
    return;
}
void find(ll rt,ll l,ll r,ll L,ll R)
{
    if(l>=L&&r<=R)
    {
        ans[c]+=su[rt];
    }
    else
    {
        if(o[rt]!=)
        {
            su[rt*]+=o[rt]*((r+l)/-l+);
            su[rt*+]+=o[rt]*(r-(r+l)/);
            o[rt*]+=o[rt];
            o[rt*+]+=o[rt];
            o[rt]=;
        }
        if(L<=(l+r)/)
        {
            find(ls,L,R);
        }
        if(R>(l+r)/)
        {
            find(rs,L,R);
        }
        su[rt]=su[*rt]+su[*rt+];
    }
    return;
}
int main()
{
    scanf("%d %d",&n,&m);//n个基本点，m次操作
    build(,,n);
    for(int i=;i<=m;i++)
    {
        scanf("%d",&a);
        if(a==)//我们要进行区间加啦
        {
            scanf("%lld %lld %lld",&x,&y,&k);//在x到y上加k
            change(,,n,x,y,k);
//            for(int i=1;i<=2*n;i++)cout<<" "<<i<<"="<<su[i];
//            cout<<"\n";
//            写给需要调试的小可爱的
        }
        if(a==)//查询
        {
            c++;//个人喜欢统一输出，c记录第几次询问
            scanf("%lld %lld",&x,&y);//查询x到y的和
            find(,,n,x,y);
        }
    }
    for(int i=;i<=c;i++)
    {
        printf("%lld\n",ans[i]);//统一输出答案
    }
}

这样，一棵完完整整的基础简化版的线段树就写完了

如果你看完上面的觉得很简单，那你可以继续学习接下来的zkw线段树了

但是如果你觉得没那么简单，一定去练几个题再回来看下面的

zkw线段树不知道比递归线段树快到哪里去了，跑得嗷嗷的

看不懂就画图，手模

n是数组大小

单点修改 区间求和

#include<iostream>
#include<cstdio>
using namespace std;
int n,m,q,ans,l,r;
int t[];
char q1[];
void build()//非递归建树，从m+1开始，多余的空间我不要了（任性）
{
    for(m=;m<=n+;m<<=);
    for(int i=m+;i<=m+n;i++) scanf("%d",&t[i]);
    for(int i=m-;i>=;i--) t[i]=t[i<<]+t[i<<|];
}
void change(int x,int a)//这个不能再短
{
    for(x+=m;x;x>>=) t[x]+=a;
}
void ask(int l,int r)
{
    for(l+=m-,r+=m+;l^r^;l>>=,r>>=)
    {
        if(~l&)ans+=t[l^];
        if(r&) ans+=t[r^];
    }
    printf("%d\n",ans);
}
int main()//按需填写
{
    ...
}

区间修改 区间求和

#include<iostream>
#include<cstdio>
using namespace std;
void build()//建树一样的
{
    for(m=;m<=n+;m<<=);
    for(int i=m+;i<=m+n;i++) scanf("%d",&t[i]);
    for(int i=m-;i>=;i--) t[i]=t[i<<]+t[i<<|];
}
void change(int l,int r,int k)//标记不下传，永久化
{
    int ln=;//左指针走了多少了
    int rn=;//右指针走了多少了
    int nn=;//这层的点的子树多大
    for(l+=m-,r+=m+;l^r^;l>>=,r>>=,nn<<=)//这里是开区间
    {
        t[l]+=k*ln;
        t[r]+=k*rn;
        if(~l&)//左指针是左儿子，兄弟该被修改
        {
            add[l^]+=k;
            t[l^]+=k*nn;
            ln+=nn;
        }
        if(r&)//右指针是右儿子，同理
        {
            add[r^]+=k;
            t[r^]+=k*nn;
            rn+=nn;
        }
    }
    for(;l;l>>=,r>>=)//加到底
    {
        t[l]+=k*ln;
        t[r]+=k*rn;
    }
}
void ask(int l,int r)
{
    int ln=;
    int rn=;
    int nn=;
    int ans=;
    for(l+=m-,r+=m+;l^r^;l>>=,r>>=,nn<<=)//注意nn
    {
        if(add[l]) ans+=add[l]*ln;
        if(add[r]) ans+=add[r]*rn;
        if(~l&)
        {
            ans+=t[l^];
            ln+=nn;
        }
        if(r&)
        {
            ans+=t[r^];
            rn+=nn;
        }
    }
    for(;l;l>>=,r>>=)//加到底
    {
        ans+=add[l]*ln;
        ans+=add[r]*rn;
    }
}
int main()
{
    ...
}

区间修改 区间最值

#include<iostream>
#include<cstdio>
using namespace std;
int l,r,n,q,m,ans,k,a;
int t[];
void build()
{
    for(m=;m<=n+;m<<=);
    for(int i=m+;i<=m+n;i++) scanf("%d",&t[i]);
    for(int i=m-;i>=;i--)//区间最值有优化，建树和区间求和不一样
    {
        t[i]=min(t[i<<],t[i<<|]);//类似差分
        t[i<<]-=t[i];
        t[i<<|]-=t[i];
    }
}
void change(int l,int r,int k)
{
    int tmp;
    for(l+=m-,r+=m+;l^r^;l>>=,r>>=)
    {
        if(~l&)t[l^]+=k;
        if(r&) t[r^]+=k;
        tmp=min(t[l],t[l^]);//继续差分
        t[l]-=tmp;
        t[l^]-=tmp;
        t[l>>]+=tmp;
        tmp=min(t[r],t[r^]);
        t[r]-=tmp;
        t[r^]-=tmp;
        t[r>>]+=tmp;
    }
    for(;l!=;l>>=)//差分到底
    {
        tmp=min(t[l],t[l^]);
        t[l]-=tmp;
        t[l^]-=tmp;
        t[l>>]+=tmp;
    }
}
void ask(int l,int r)
{
    lans=;
    rans=;
    if(l!=r)
    {
        for(l+=m,r+=m;l^r^;l>>=,r>>=)
        {
            lans+=t[l];
            rans+=t[r];
            if(~l&)lans=min(t[l^],lans);
            if(r&) rans=min(t[r^],rans);
        }
    }
    ans=min(lans+t[l],rans+t[r]);
    while(s>) ans+=t[s>>=];//一定要到底
    printf("%d\n",ans);
}
int main()
{
    ...
}

有问题的话可以问呦~虽然我也不一定会但是我会尽力解答的！

感谢阅读，求赞