【分治】peak find

分治算法

算法设计中一种常用的优化方法就是分治的思想，它的解决思路就是将原始的问题划分为性质一样，但是规模减小的子问题，然后通过子问题的解和合并子问题的解得到最终的解，就是分治的思想；

比较常见的分治有 归并排序算法，快速排序算法，两种都是优化的排序算法；

归并排序

归并排序算法通过将问题划分为左半部分、右半部分问题的解决，然后通过合并有序的左半部分、有序的右半部分使得最终有序。所以假设问题的求解时间复杂度为 T（n） = 2*T（n/2） + C（n），其中T（n）表示长度为n的归并排序复杂度，等于两个子问题的复杂度和合并两个有序序列的复杂度C（n），C（n）代表一个关于n的常数项复杂度，最终时间复杂度nlog(n)，

快速排序

快速排序的思想和归并排序的思想比较类似，随机找到一个partition把数组划分为比它小的部分，比它大的部分，然后依次使用这种思想继续划分其左半部分，右半部分，但是不能保证每次都能够将问题规模正好的切分为两个相同的，所以平均时间复杂度为nlog(n)，最坏的时间复杂度为n^2（每次的patition元素选择都很糟糕）

切入正题，使用分治的两个算法题目

一维数组的局部最大值查找

题目描述：在一个整数数组中查找一个数，该数大于等于其左边的元素、并且大于等于其右边的元素（假定数组最边界是极小值，即-1，n的索引位置为Integer.MIN_VALUE）

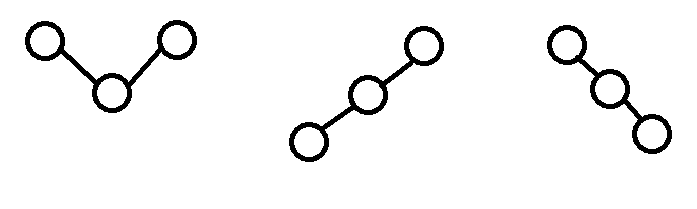
举例：[1,2,3,4,5]则返回5， [1,3,2,4,3,5]中返回3,4,5任意一个；

思路：

逐个遍历可以查找到所有的局部最大值，但是时间复杂度O（n），题目要求找到一个即可，所以应该有优化的空间。

能够比n更优化的很容易想到二分的思路，所以顺着这个思路，首先找到mid元素，如果mid元素满足局部最大值，直接返回，不满足？

以下三种情况，此时选择最大的那一半继续二分查找即可，因为最大的那一边必定包含一个局部最大值

	public int peekFind1(int[] array) {
		int len = array.length;
		//len == 0 exception
		int l = 0, r = len - 1;
		while(r > l) {
			int m = l + (r - l)/2;
			if( (m - 1 < 0 || array[m] >= array[m-1]) && (m + 1 >= len || array[m] >= array[m+1]) ) {
				return array[m];
			}
			else if( (m - 1 >= 0 && array[m-1] > array[m]) ) {
				r = m-1;
			}
			else {
				l = m+1;
			}
		}
		return array[r];
	}

二维数组的局部最大值查找

题目描述：在一个二维整数数组中查找一个数，该数大于等于其上、下、左、右的元素（假定数组最边界是极小值）

思路：

逐个遍历可以查找到所有的局部最大值，但是时间复杂度O（n^2），题目要求找到一个即可，所以应该有优化的空间。

二维数组的扩展正常的思路可能会想着借助一维数组已有的解决方案去解决这个题目，但是这么想可能就会陷入死胡同，

比如针对每行使用刚才一维的解决方案，找到每行的局部最大值，好像并没有什么帮助，

在针对每列使用刚才一维的解决方案，找到每列的局部最大值，但是没办法保证与刚才每行的有重叠？

所以想利用一维的算法求出每列或者每行的最大值，此时在最大值的以为数组中使用一维的解决方案即可，但是求解每列或者每行的最大值使得问题复杂度达到O（n^2）了；

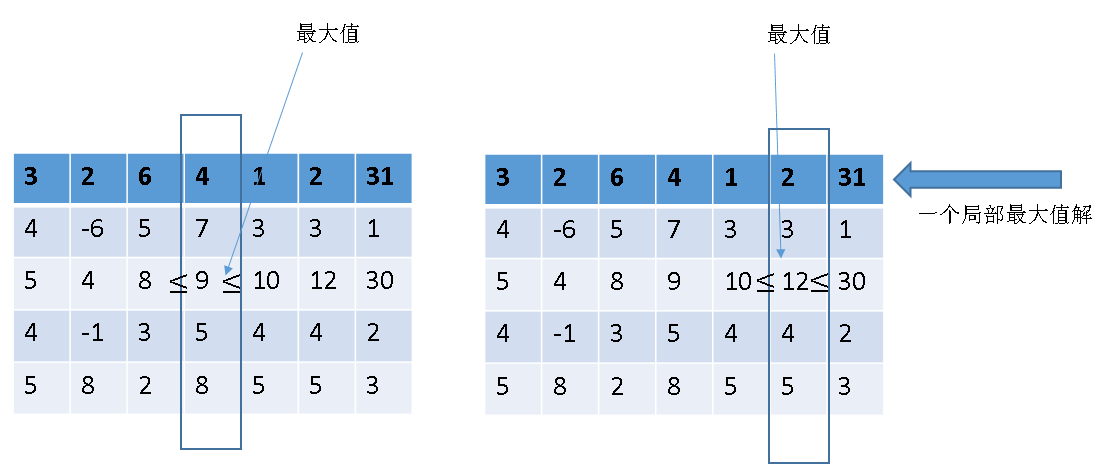
所以思路回退到分治的策略，比如先找到中间一列的最大值，这个值必定大于其上下，然后查看这个值左右的情况，如果满足局部最大值，直接返回，不满足？

同样是上面的三种情况，选择有更大元素的那半边继续采用这种思想求解即可得到答案，时间复杂度nlog(n)，

图解：

	public int maxNum(int[] array) {
		int result = array[0];
		int idx = 0;
		for(int i = 1;i < array.length;i++) {
			if(array[i] > result) {
				result = array[i];
				idx = i;
			}
		}
		return idx;
	}
	public int peekFind2(int[][] matrix) {
		int row = matrix.length;
		//row == 0 exception
		int column = matrix[0].length;
		if(row == 1) return peekFind1(matrix[0]);
		if(column == 1) {
			int[] array = new int[row];
			for(int i = 0;i < row;i++) array[i] = matrix[i][0];
			return peekFind1(array);
		}
		int startR = 0, endR = row - 1;
		while(endR > startR) {
			int midR = startR + (endR - startR)/2;
			int maxIdx = maxNum(matrix[midR]);
			if( (midR - 1 < 0 || matrix[midR][maxIdx] >= matrix[midR - 1][maxIdx]) && (midR + 1 >= row || matrix[midR][maxIdx] >= matrix[midR + 1][maxIdx]) ) {
				return matrix[midR][maxIdx];
			}
			else if( (midR - 1 >= 0 && matrix[midR - 1][maxIdx] > matrix[midR][maxIdx]) ) {
				endR = midR - 1;
			}
			else {
				startR = midR + 1;
			}
		}
		return matrix[startR][maxNum(matrix[startR])];
	}

针对二维的局部最大值求解存在O（n）时间复杂度的解决方案，这个后面再分享，思考算法的时候尽可能的发散思维，不能僵化住自己的思想。

如果发现上面有什么错误，欢迎指正。