bzoj 3653 [湖南集训]谈笑风生

题目描述

设 T 为一棵有根树，我们做如下的定义：

• 设 a 和 b 为 T 中的两个不同节点。如果 a 是 b 的祖先，那么称“a 比 b 不知道高明到哪里去了”。

• 设 a 和 b 为 T 中的两个不同节点。如果 a 与 b 在树上的距离不超过某个给定常数 x，那么称“a 与 b 谈笑风生”。

给定一棵 n 个节点的有根树 T，节点的编号为 1 ∼ n，根节点为 1 号节点。你需要回答 q 个询问，询问给定两个整数 p 和 k，问有多少个有序三元组 (a; b; c) 满足：

1. a、 b 和 c 为 T 中三个不同的点，且 a 为 p 号节点；

2. a 和 b 都比 c 不知道高明到哪里去了；

3. a 和 b 谈笑风生。这里谈笑风生中的常数为给定的 k。

输入输出格式

输入格式：

输入文件的第一行含有两个正整数 n 和 q，分别代表有根树的点数与询问的个数。

接下来 n − 1 行，每行描述一条树上的边。每行含有两个整数 u 和 v，代表在节点 u 和 v 之间有一条边。

接下来 q 行，每行描述一个操作。第 i 行含有两个整数，分别表示第 i 个询问的 p 和 k。

输出格式：

输出 q 行，每行对应一个询问，代表询问的答案。

输入输出样例

输入样例#1：

5 3
1 2
1 3
2 4
4 5
2 2
4 1
2 3

输出样例#1：

3
1
3

说明

样例中的树如下图所示：

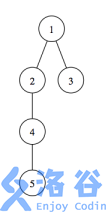
对于第一个和第三个询问，合法的三元组有 (2,1,4)、 (2,1,5) 和 (2,4,5)。

对于第二个询问，合法的三元组只有 (4,2,5)。

所有测试点的数据规模如下：

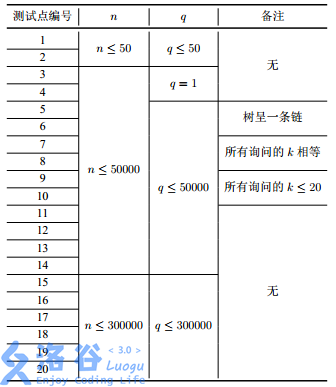
对于全部测试数据的所有询问， 1 ≤ p ≤ n， 1 ≤ k ≤ n.

今天是长者的生日，所以要谈笑风生。。。

首先a是固定的，那么分两种情况讨论b的位置：

1.b是a的祖先，这样的贡献是:

2.b在a的子树内，且b是c的祖先，那么我们枚举每一个可能的深度计算答案，那么贡献为：

(size-1是因为要三个点不同)

也就是要维护某个深度的size和，然后因为有dfn的限制，我们可以用可持久化线段树来实现维护。。。

那么我们按照dfn来建主席树，主席树以deep为值域，然后询问就是在主席树上区间求和即可。。。

// MADE BY QT666
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<iostream>
#include<cstring>
using namespace std;
typedef long long ll;
const int N=600050;
int to[N],nxt[N],head[N],cnt;
int dfn[N],ed[N],tt,size[N],deep[N],xh[N];
int rt[N*20],rs[N*20],ls[N*20],sz,n,q;
ll sum[N*20];
void lnk(int x,int y){
  to[++cnt]=y,nxt[cnt]=head[x],head[x]=cnt;
  to[++cnt]=x,nxt[cnt]=head[y],head[y]=cnt;
}
void dfs(int x,int f){
  size[x]=1;deep[x]=deep[f]+1;dfn[x]=++tt,xh[tt]=x;
  for(int i=head[x];i;i=nxt[i]){
    int y=to[i];if(y==f) continue;dfs(y,x);size[x]+=size[y];
  }
  ed[x]=tt;
}
void insert(int x,int &y,int l,int r,int id,int v){
  y=++sz;ls[y]=ls[x];rs[y]=rs[x];sum[y]=sum[x];
  if(l==r){sum[y]+=v;return;}
  int mid=(l+r)>>1;
  if(id<=mid) insert(ls[x],ls[y],l,mid,id,v);
  else insert(rs[x],rs[y],mid+1,r,id,v);
  sum[y]=sum[ls[y]]+sum[rs[y]];
}
ll query(int x,int y,int l,int r,int xl,int xr){
  if(xl<=l&&r<=xr) return sum[y]-sum[x];
  int mid=(l+r)>>1;
  if(xr<=mid) return query(ls[x],ls[y],l,mid,xl,xr);
  else if(xl>mid) return query(rs[x],rs[y],mid+1,r,xl,xr);
  else return query(ls[x],ls[y],l,mid,xl,mid)+query(rs[x],rs[y],mid+1,r,mid+1,xr);
}
int main(){
  scanf("%d%d",&n,&q);
  for(int i=1;i<n;i++){
    int u,v;scanf("%d%d",&u,&v);lnk(u,v);
  }
  dfs(1,1);
  for(int i=1;i<=tt;i++) insert(rt[i-1],rt[i],1,2*n,deep[xh[i]],size[xh[i]]-1);
  for(int i=1;i<=q;i++){
    int x,k;scanf("%d%d",&x,&k);
    ll ans=1ll*min(deep[x]-1,k)*(size[x]-1);
    ans+=query(rt[dfn[x]-1],rt[ed[x]],1,2*n,deep[x]+1,deep[x]+k);
    printf("%lld\n",ans);
  }
  return 0;
}