MATLAB卷积运算（conv、conv2、convn）解释

1

conv（向量卷积运算）

所谓两个向量卷积，说白了就是多项式乘法。
比如:p=[1 2 3],q=[1 1]是两个向量，p和q的卷积如下：
把p的元素作为一个多项式的系数，多项式按升幂（或降幂）排列，比如就按升幂吧，写出对应的多项式：1+2x+3x^2;同样的，把q的元素也作为多项式的系数按升幂排列，写出对应的多项式：1+x。

卷积就是“两个多项式相乘取系数”。
（1+2x+3x^2）×（1+x）=1+3x+5x^2+3x^3
所以p和q卷积的结果就是[1 3 5 3]。

记住，当确定是用升幂或是降幂排列后，下面也都要按这个方式排列，否则结果是不对的。
你也可以用matlab试试
p=[1 2 3]
q=[1 1]
conv(p,q)
看看和计算的结果是否相同。

conv2（二维矩阵卷积运算）

a=[1 1 1;1 1 1;1 1 1];
b=[1 1 1;1 1 1;1 1 1];
>> conv2(a,b)

ans =

1     2     3     2     1
     2     4     6     4     2
     3     6     9     6     3
     2     4     6     4     2
     1     2     3     2     1

>> conv2(a,b,'valid')

ans =

9

>> conv2(a,b,'same')

ans =

4     6     4
     6     9     6
     4     6     4

>> conv2(a,b,'full')

ans =

1     2     3     2     1
     2     4     6     4     2
     3     6     9     6     3
     2     4     6     4     2
     1     2     3     2     1

convn（n维矩阵卷积运算）

>> a=ones(5,5,5)

a(:,:,1) =

1     1     1     1     1
     1     1     1     1     1
     1     1     1     1     1
     1     1     1     1     1
     1     1     1     1     1

a(:,:,2) =

1     1     1     1     1
     1     1     1     1     1
     1     1     1     1     1
     1     1     1     1     1
     1     1     1     1     1

a(:,:,3) =

1     1     1     1     1
     1     1     1     1     1
     1     1     1     1     1
     1     1     1     1     1
     1     1     1     1     1

a(:,:,4) =

1     1     1     1     1
     1     1     1     1     1
     1     1     1     1     1
     1     1     1     1     1
     1     1     1     1     1

a(:,:,5) =

1     1     1     1     1
     1     1     1     1     1
     1     1     1     1     1
     1     1     1     1     1
     1     1     1     1     1

>> b=ones(5,5,5);

>> convn(a,b,'valid')

ans =

125

>> convn(a,b,'same')

ans(:,:,1) =

27    36    45    36    27
    36    48    60    48    36
    45    60    75    60    45
    36    48    60    48    36
    27    36    45    36    27

ans(:,:,2) =

36    48    60    48    36
    48    64    80    64    48
    60    80   100    80    60
    48    64    80    64    48
    36    48    60    48    36

ans(:,:,3) =

45    60    75    60    45
    60    80   100    80    60
    75   100   125   100    75
    60    80   100    80    60
    45    60    75    60    45

2

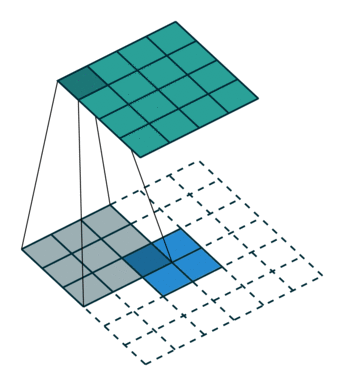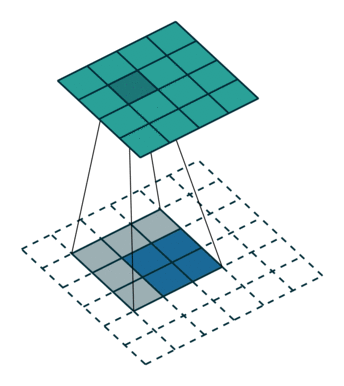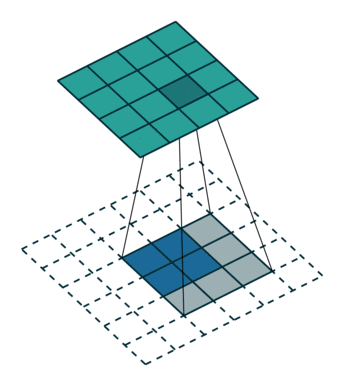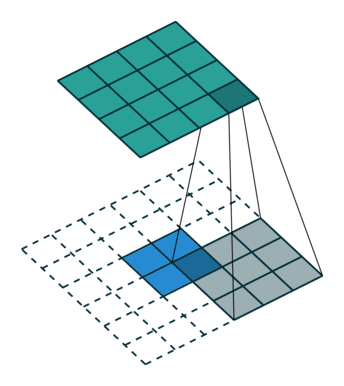
1.full

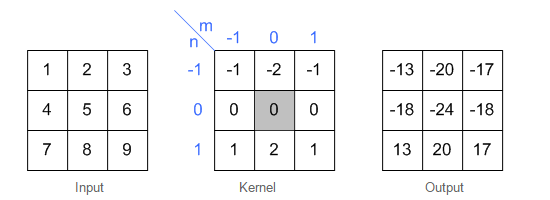
如下图：

图（1）

图中蓝色为原图像，白色为对应卷积所增加的padding，通常全部为0，绿色是卷积后图片。图的卷积的滑动是从卷积核右下角与图片左上角重叠开始进行卷积，滑动步长为1，卷积核的中心元素对应卷积后图像的像素点。

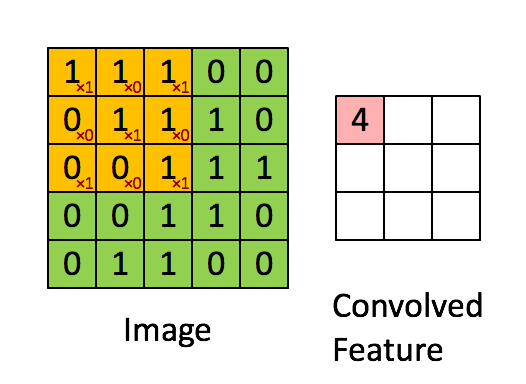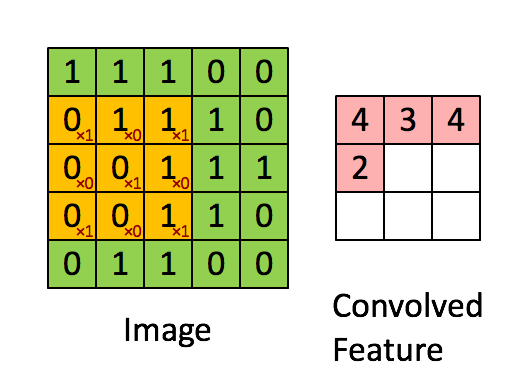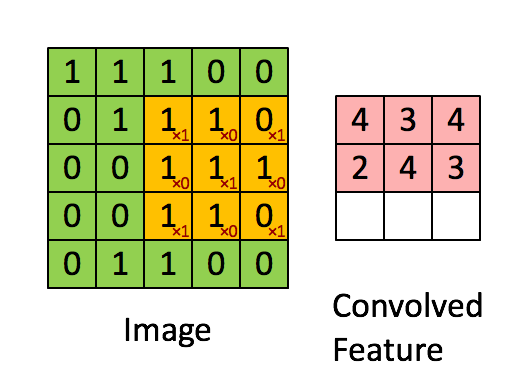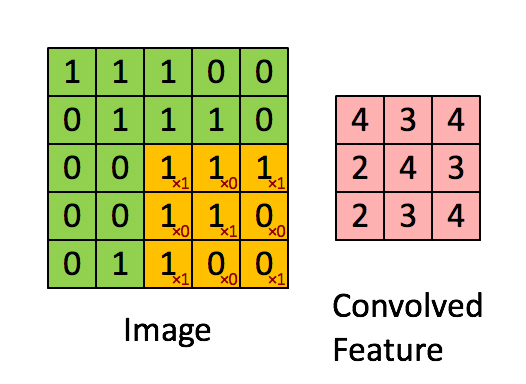
2.same

如下图：

图（2）

卷积的时候需要对卷积核进行180的旋转，同时卷积核中心与需计算的图像像素对齐，输出结构为中心对齐像素的一个新的像素值

3. valid

如下图：

图（3）

太简单，不解释。

最后，我们可以总结出full，same，valid三种卷积后图像大小的计算公式：

1.full: 滑动步长为1，图片大小为N1xN1，卷积核大小为N2xN2，卷积后图像大小：N1+N2-1 x N1+N2-1

如图1， 滑动步长为1，图片大小为2x2，卷积核大小为3x3，卷积后图像大小：4x4

2.same: 滑动步长为1，图片大小为N1xN1，卷积核大小为N2xN2，卷积后图像大小：N1xN1

3.valid:滑动步长为S，图片大小为N1xN1，卷积核大小为N2xN2，卷积后图像大小：(N1-N2)/S+1 x (N1-N2)/S+1

如图2，滑动步长为1，图片大小为5x5，卷积核大小为3x3，卷积后图像大小：3x3

 

3

MATLAB的conv2函数实现步骤（conv2（A,B））：

其中，矩阵A和B的尺寸分别为ma*na即mb*nb

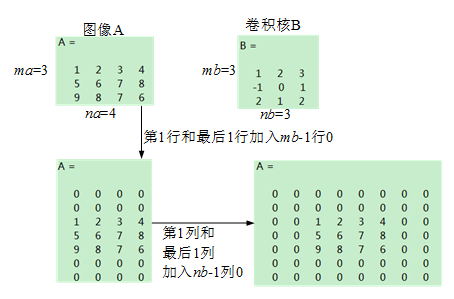
① 对矩阵A补零，第一行之前和最后一行之后都补mb-1行，第一列之前和最后一列之后都补nb-1列（注意conv2不支持其他的边界补充选项，函数内部对输入总是补零）；

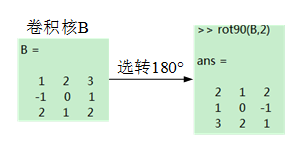
② 将卷积核绕其中心旋转180度；

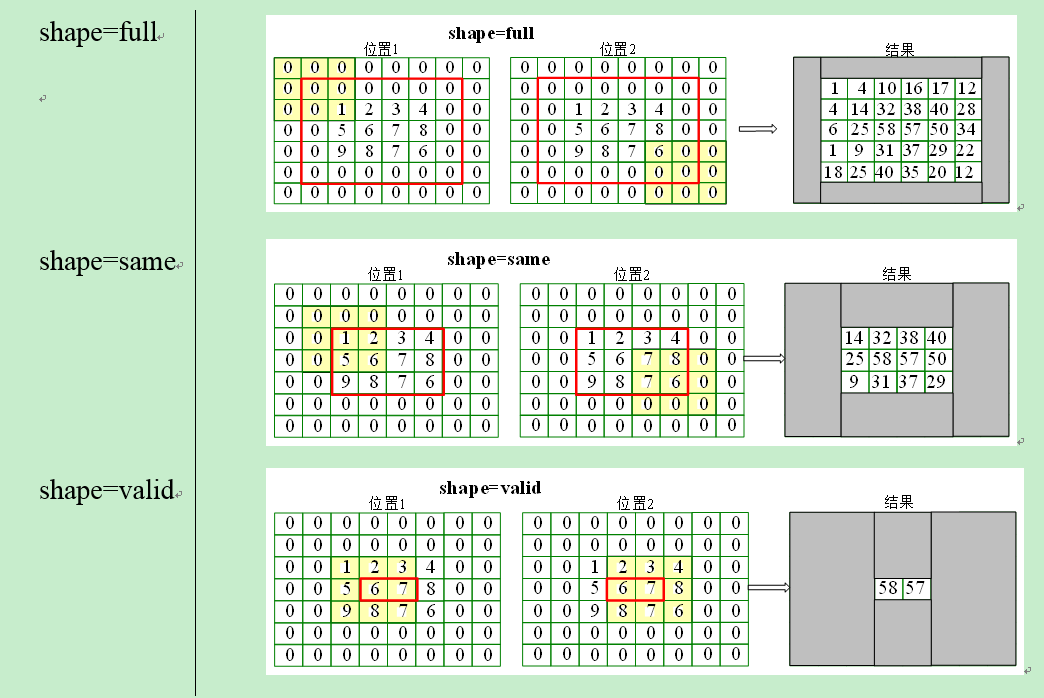
③ 滑动旋转后的卷积核，将卷积核的中心位于图像矩阵的每一个元素，并求乘积和（即将旋转后的卷积核在A上进行滑动，然后对应位置相乘，最后相加）；下面分别是shape=full, same, valid时取输出图像大小的情况，其中：位置1表示输出图像的值从当前核的计算值开始（对应输出图像左上角），位置2表示到该位置结束（对应输出图像右下角）