最小生成树（图论）--3366lg【模版】

题目描述

如题，给出一个无向图，求出最小生成树，如果该图不连通，则输出orz

输入输出格式

输入格式：

第一行包含两个整数N、M，表示该图共有N个结点和M条无向边。（N<=5000，M<=200000）

接下来M行每行包含三个整数Xi、Yi、Zi，表示有一条长度为Zi的无向边连接结点Xi、Yi

输出格式：

输出包含一个数，即最小生成树的各边的长度之和；如果该图不连通则输出orz

输入输出样例

输入样例#1：复制

输出样例#1：复制

说明

时空限制：1000ms,128M

数据规模：

对于20%的数据：N<=5，M<=20

对于40%的数据：N<=50，M<=2500

对于70%的数据：N<=500，M<=10000

对于100%的数据：N<=5000，M<=200000

样例解释：

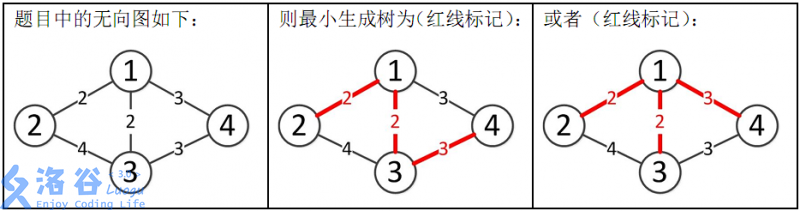
所以最小生成树的总边权为2+2+3=7

---------------------------------------------------这是分割线----------------------------------------------------------------

下面是算法介绍

Kruskal算法

1.概览

Kruskal算法是一种用来寻找最小生成树的算法，由Joseph Kruskal在1956年发表。用来解决同样问题的还有Prim算法和Boruvka算法等。三种算法都是贪婪算法的应用。和Boruvka算法不同的地方是，Kruskal算法在图中存在相同权值的边时也有效。

2.算法简单描述

1).记Graph中有v个顶点，e个边

2).新建图Graph_new，Graph_new中拥有原图中相同的e个顶点，但没有边

3).将原图Graph中所有e个边按权值从小到大排序

4).循环：从权值最小的边开始遍历每条边直至图Graph中所有的节点都在同一个连通分量中

if 这条边连接的两个节点于图Graph_new中不在同一个连通分量中

添加这条边到图Graph_new中

图例描述：

首先第一步，我们有一张图Graph，有若干点和边

将所有的边的长度排序，用排序的结果作为我们选择边的依据。这里再次体现了贪心算法的思想。资源排序，对局部最优的资源进行选择，排序完成后，我们率先选择了边AD。这样我们的图就变成了右图

在剩下的变中寻找。我们找到了CE。这里边的权重也是5

依次类推我们找到了6,7,7，即DF，AB，BE。

下面继续选择， BC或者EF尽管现在长度为8的边是最小的未选择的边。但是现在他们已经连通了（对于BC可以通过CE,EB来连接，类似的EF可以通过EB,BA,AD,DF来接连）。所以不需要选择他们。类似的BD也已经连通了（这里上图的连通线用红色表示了）。

最后就剩下EG和FG了。当然我们选择了EG。最后成功的图就是右：

3.简单证明Kruskal算法

对图的顶点数n做归纳，证明Kruskal算法对任意n阶图适用。

归纳基础：

n=1，显然能够找到最小生成树。

归纳过程：

假设Kruskal算法对n≤k阶图适用，那么，在k+1阶图G中，我们把最短边的两个端点a和b做一个合并操作，即把u与v合为一个点v'，把原来接在u和v的边都接到v'上去，这样就能够得到一个k阶图G'(u,v的合并是k+1少一条边)，G'最小生成树T'可以用Kruskal算法得到。

我们证明T'+{<u,v>}是G的最小生成树。

用反证法，如果T'+{<u,v>}不是最小生成树，最小生成树是T，即W(T)<W(T'+{<u,v>})。显然T应该包含<u,v>，否则，可以用<u,v>加入到T中，形成一个环，删除环上原有的任意一条边，形成一棵更小权值的生成树。而T-{<u,v>}，是G'的生成树。所以W(T-{<u,v>})<=W(T')，也就是W(T)<=W(T')+W(<u,v>)=W(T'+{<u,v>})，产生了矛盾。于是假设不成立，T'+{<u,v>}是G的最小生成树，Kruskal算法对k+1阶图也适用。

由数学归纳法，Kruskal算法得证。

-----------------------------------又是一条分割线--------------------------------------------------------------------------

其实

很好弄懂的

而且

这个模版题

真的很基础很基础

但是

我还是写了好久

主要原因吧

还是掌握不牢

逻辑经常搞乱

要多刷几道才可以哇

---------------------------------又又又是分割线----------------------------------------------------------------------------

#include<cstdio>
#include<algorithm>
using namespace std;

int n,m,ans; //ans累计最小生成树的总长
int fa[200000]; //为每一个节点的父节点开一个数组；

struct mo
{
int x,y,z;
}a[200000]; //开一个结构体 z是一条边 x是（起）节点 y是（末）节点备注因为是无向树所以其实是没有方向的但为了好区分才分成（起末）

bool cmp(mo x,mo y)
{
return x.z<y.z;
} //纯是为了sort排序用的将每一条边的长度排序

int getfa(int x) //寻找根节点（最大的boss）
{
if(fa[x] == x)
return fa[x]; //如果某一个节点的父节点就是他自己的话他自己本身就是根节点（自己就是最大的boss）
else
return fa[x]=getfa(fa[x]); //它的根节点就是它父节点的根（父节点的父节点的....）节点
} //这样每一个节点的根节点就知道了就可以很容易的判断出来某两个节点是不是同根的

/*void merge(int x,int y)
{
int s1=getfa(x),s2=getfa(y);
if(s1 == s2)
return;
else
if(s1<s2)
fa[x]=s2;
else
fa[y]=s1;
}
*/
int main()
{
scanf("%d%d",&n,&m); //n个节点 m个边
for(int i=1;i<=m;i++)
{
scanf("%d%d%d",&a[i].x,&a[i].y,&a[i].z); //按边的数量循环输入输入每个边的两个节点和边的长度
}

sort(a+1,a+m+1,cmp); //把边的长度排序

for(int i=1;i<=n;i++)
{
fa[i]=i; //先让每一个节点的父节点（根节点都是自己）
}

for(int i=1;i<=m;i++)
{
int l=getfa(a[i].x);
int r=getfa(a[i].y);
if(l != r) //比较同一个边的根节点不相同就合并也只有两个节点的根节点不相同的边才可取
{
fa[l]=r;
ans+=a[i].z;
} //根节点相同的不可取
}
if(ans != 0)
printf("%d",ans);
else
printf("orz");
return 0;
}