U盘从Fat32快速转换为NTFS
WIN+R ,输入cmd,打开命令框
输入: convert d:/FS:NTFS
注意,你的U盘的盘符是什么就写什么,我的是d盘
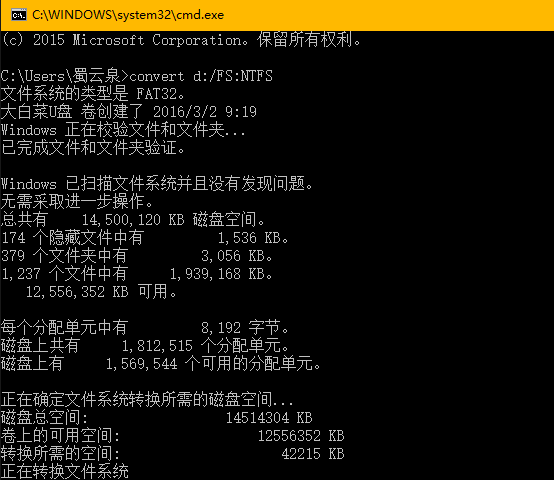
例外的来了!!!一般来说,按照我上面的步骤已经没有问题了。但是!!!问题总是层出不穷的。下面来介绍一种问题。
恩,是这样的,按照上面的方法输入完成之后呢它要我输入当前卷标....问题如图:

你如果不知道输入什么的话就会说你输入的不正确。。。
解决方法:
改名!!!
把你的U盘改名,例如我改成了W(单机右键重命名....)

然后呢,它再让我输入名字,我就只需要输入W就可以了。然后看结果:

可以了

U盘从Fat32快速转换为NTFS的更多相关文章
- U盘用FAT32还是用NTFS格式好
U盘用FAT32还是用NTFS格式好 ● FAT32文件系统 FAT32使用4个字节(也就是32位)的空间来表示每个扇区(Sector)配置文件的情形,故称之为FAT32.FAT16的分区容量上限是2 ...
- 在cmd中将FAT32转换为NTFS分区的命令是什么?
将FAT32转换为NTFS分区的命令是什么? ========================================== 在cmd命令行模式下输入: convert x: /fs:ntfs ...
- 将磁盘从FAT格式转换为NTFS格式的方法
不需要进行格式化,只需在命令提示符中输入如下内容:CONVERT X:/FS:NTFS把X换成你需要的盘符,转一个盘需十几或几十秒不等..注意:此方法不可逆转,FAT32转到NTFS后不可转回,当然也 ...
- 【转载】C#使用ToList()将数组快速转换为List集合
在C#的编程中,数组和List集合是比较常用的两个集合类,有时候因为业务需要,需要将数组集合转换为List集合,此时就可以使用C#中的Linq的扩展方法ToList方法来实现,只需要简单的一条语句即可 ...
- IOS 字典快速转换为Model 模型
一般情况下IOS得局部页面加载的过程是,创建一个Model然后,将Nib文件与Model进行关联,然后能够快速的获取到Nib文件上的控件实例.操作生成页面. 但是原生的内容是没有直接通过Json获取M ...
- 三星笔记本进入BIOS后找不到U盘启动项/快速启动键F12没有反应
分析:BIOS开启了 Fast Bios Mode 解决方法: 开机按F2进入BIOS设置,选择Advanced菜单下Fast Bios Mode,设置为 Disabled,按F10键保存退出,重启时 ...
- FAT32格式和NTFS格式区别
NTFS(Windows):支持最大分区2TB,最大文件2TB: FAT16(Windows):支持最大分区2GB,最大文件2GB: FAT32(Windows):支持最大分区128GB,最大文件4G ...
- 盘符格式转换成NTFS格式
点击屏幕左下角“开始”,找到运行,在其中输入:cmd,确定,打开“命令提示符”; 在命令提示符下输入: convert X:/FS:NTFS(其中X是你要转换的盘符盘符). 执行后,重新启动电脑 这样 ...
- word文档快速转换为PPT演示文稿
方法一: 访问http://t.im/pdftoppt,点击继续浏览(会跳转至:https://smallpdf.com/cn/pdf-to-ppt): 打开word文档,设置为“横向”,输出为PDF ...
随机推荐
- python 中的列表(list)
一.生成一个列表 直接生成 L1 = [1, 2, 3, 4, 5] 列表解析式 >>> L2 = [x for x in range(1, 10, 2)] #从1到10的迭代,步长 ...
- 现代程序设计 homework-02
首先显示博客要求: 描述在这么多相似的需求面前, 你怎么维护你的设计 (父类/子类/基类, UML, 设计模式, 或者其它方法) 让整个程序的架构不至于崩溃的? 建议从后往前来搞,比如我通读一遍需求 ...
- 第八章Jdk代理 cglib代理
什么是代理模式 代理(Proxy)是一种设计模式,提供了对目标对象另外的访问方式;即通过代理对象访问目标对象.这样做的好处是:可以在目标对象实现的基础上,增强额外的功能操作,即扩展目标对象的功能. 这 ...
- Docker Clustering Tools Compared: Kubernetes vs Docker Swarm
https://technologyconversations.com/2015/11/04/docker-clustering-tools-compared-kubernetes-vs-docker ...
- asp.net core 2.0中的配置(1)---Configuration
配置就是一个装配数据字典的过程,一个字典也就是一个键值对,所以从配置就是键值对. 在asp.net core中关于配置是由四个基本的类型来支撑的,是①IConfigurationSource②ICon ...
- Linux shell 菜鸟学习笔记....
20171123 Linux shell 基础学习笔记1. shell 的开始 一般是 #!/bin/bash 通过 #! 来唯一指定使用的shell路径 其他的 # 都表示注释.2. shell 的 ...
- [读书笔记]Linux命令行与shell编程读书笔记02 环境变量以及其他
1. Linux的环境变量. 全局环境变量的查看 printenv 一个结果示例 XDG_SESSION_ID=354TERM=xtermSHELL=/bin/bashSSH_CLIENT=10.24 ...
- K3CLOUD新增用户
1.在金蝶云之家对应的产品序列中新增用户 2.在CLOUD本地查询用户-同步注册用户后,云平台用户会同步至本地
- os模块+sys模块+random模块+shutil模块
os.getcwd() 获取当前工作目录,即当前python脚本工作的目录路径os.chdir("dirname") 改变当前脚本工作目录:相当于shell下cdos.curdir ...
- poj 3694 Network(割边+lca)
题目链接:http://poj.org/problem?id=3694 题意:一个无向图中本来有若干条桥,有Q个操作,每次加一条边(u,v),每次操作后输出桥的数目. 分析:通常的做法是:先求出该无向 ...
