OO第一单元自白

Homework 1  简单多项式导函数

对于初次接触的OO，第一次作业已经可以体会到其与面向过程的C语言之间的差别。

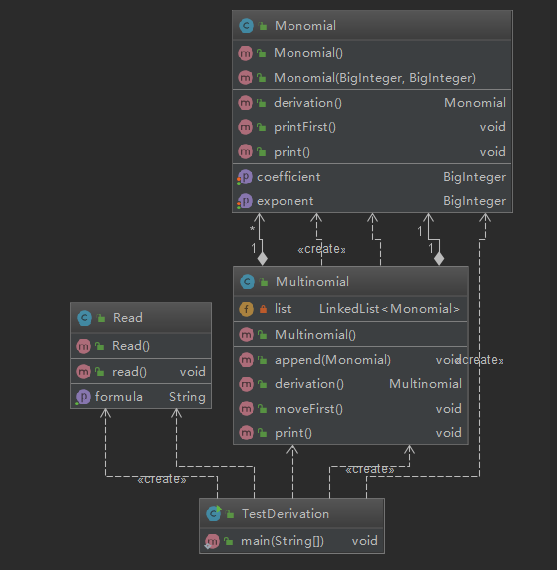
我的想法是，建立了Multinomial和Monomial 两个类，分别能够实现多项式和单项式。

对于多项式类，只提供默认的无参数构造方法。对单项式类，提供参数为系数和指数的构造方法。

个人认为，多项式的append方法是我的设计中较好的一个方法，通过将单项式append进入，将组合为一个多项式。并且，在append方法中，还拥有合并同类项的作用。

对于求导，在单项式和多项式都拥有求导方法。单项式求导返回单项式，多项式求导调用单项式的求导方法，将单项式求导结果使用append添加进一个多项式即可。

也就是说，在main方法利用正则进行了各个单项式的提取，随后只需将各个单项式简单的append，再调用多项式求导方法即可得出结果。

第一次作业bug分析

在互测中，我被hack10次，主要原因在于我对输入合法性的判断上。

对于指数情况的整数与符号分离问题，对于指数出现两个符号的情况，等等问题，我在第二次作业前进行了深刻的反思，尽可能避免再次发生同样的错误。

寻找别人的bug

阅读过别人的代码，发现自己一无所获（主要是自己太菜，有很多的格式错误，导致自己也无法找到别人的格式错误）

进行了\\v\\f的攻击，以及爆栈的攻击

Homework 2  包含简单幂函数和简单正余弦函数的导函数

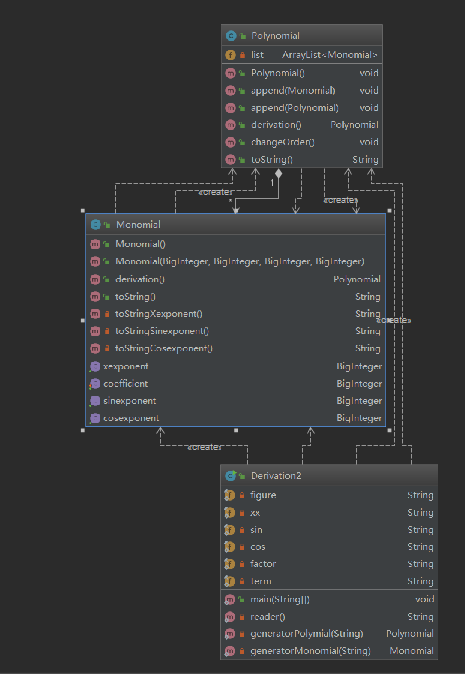
第二次作业大体延续第一次的append想法，其中有两三个主要的改动：

1.第一次作业的单项式仅仅 a * x ^ b形式，求导结果仍为这样的单项式， 但第二次作业形式 a * x ^ b * sin(x) ^ c * cos(x) ^ d，求导后由三个单项组合形成一个多项式，因此，我重载了一个参数为多项式的append方法，扩充多项式的append的参数形式既可以为单项，也可以为多项 。

2.第一次作业中我对单项式和多项式都实现了print方法，其中多项式调用单项式的print方法。但这种方法虽然能够完成第一题的要求，但较为局限。在第一次作业互测中，我发现有的同学写了toString方法，当时就觉得不错，因此第二次作业将print更改为toString，实现了输出。

3.针对第一次互测中出现的字符串格式判断进行反思，大概采取了 先判断空格相关错误->删除空格->判断多符号相关错误->化多符号为单符号 的策略

最后进行正则进行匹配于捕获。

第二次作业bug

在强测和互测中，暂未发现bug（可能还有未发现的bug）

第二次作业寻找bug

在阅读别人的代码时，我主要关注了正则的书写，并发现了一些忘记在特定地方判断空格的情况。

以及末尾出现了一个符号等等错误的情况。

 Homework 3  包含简单幂函数和简单正余弦函数的导函数

 

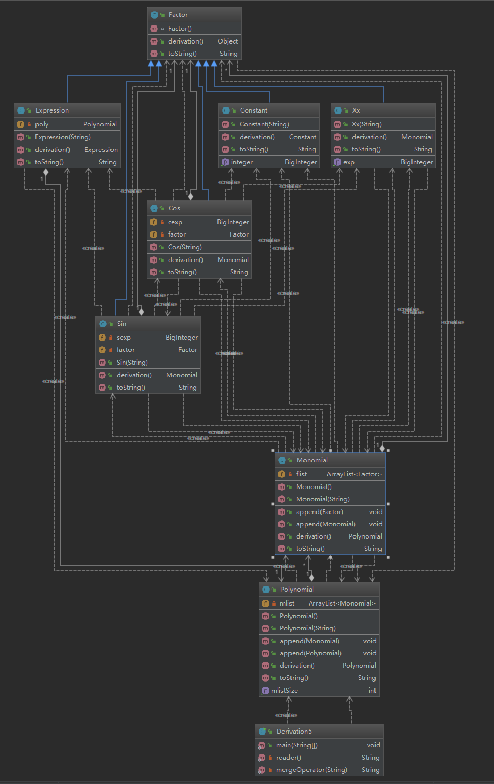
第三次的作业较为复杂，我在周六进行了一上午的思考，初步想法是使用正则，将其分为因子，分别对应到五种因子类，并且这五类继承自因子总类Factor(可以定义为抽象类)。但是，最让我崩溃的事情出现了，正则无法成对的匹配括号，于是我整个人都不好了。进度停滞。

在周日下午，有同学分享了他的作法，采用状态机的方式进行括号的分析，我深以为然，在周日晚上再次投入战斗。

具体实现方式依旧类似，不同的是，单项式里存放了因子的一个arraylist，对每种因子类，都提供了求导的方法。

我出现的bug：

在我的三角函数因子类中，我忘记匹配了指数的正负号而导致出现了错误，致使三角函数的指数出现符号无法匹配。

所幸强测中并没有。。。

怎么找别人的bug？

在没法WF的情况下用空格和TAB来找bug成为了王道。

在各种各样的可以添加的地方随意添加了几个空格和\t就发现了三个同学的bug

Applying Creational Pattern

关于第三次作业当中出现的一些问题与改进。

首先，我的判断括号的状态机直接写入了多项式类的构造方法中，导致构造方法过长，理应单独分出一个类对此进行分析操作，再将得到的结果进行对象的构造。

其次，就是我的append方法并没有进行同类项的合并，一方面是因为情况众多，比较复杂，另一方面也是时间有限，优化分数占比不高。

最后，关于各种因子类的求导问题。在我的设计中， 因子共五类，常数类，x^\d 类，sin类（sin里面可以是任意的，只要最外层是sin即可，例如sin(x),sin((x+x))等），cos类，表达式类。

常数求导还是常数类，x^\d，sin，cos求导结果为单项式类，而表达式因子类的求导结果为表达式因子类。

问题便是求导方法的返回值，对于抽象类factor，其提供的方法返回值究竟应该设定为什么？为了使得求导结果的返回值常数类或单项式类都能匹配factor类的求导方法，我竟然设定factor求导方法返回值为object类型（这样常数类和单项式类都是object子类，编译才能通过）。

其实只需要将常数类和表达式因子的返回值设定为单项式类就可以解决了。。。

如果你看到了这里，那就很感谢你啦~