机器学习简要笔记（五）——Logistic Regression(逻辑回归）

1、Logistic回归的本质
逻辑回归是假设数据服从伯努利分布，通过极大似然函数的方法，运用梯度上升/下降法来求解参数，从而实现数据的二分类。

1.1、逻辑回归的基本假设
①伯努利分布：以抛硬币为例，每次试验中出现正面的概率为P,那么出现负面的概率为1-P。那么如果假设hθ(x)为样本为正的概率，1-hθ(x)为样本为负的概率。
那么模型为hθ(x:θ)=P，并假设概率函数为Sigmoid函数

②Sigmoid函数

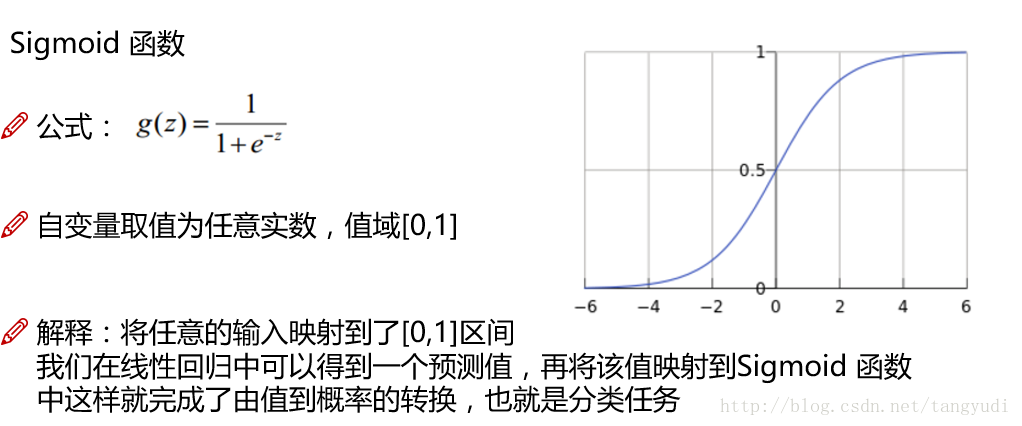
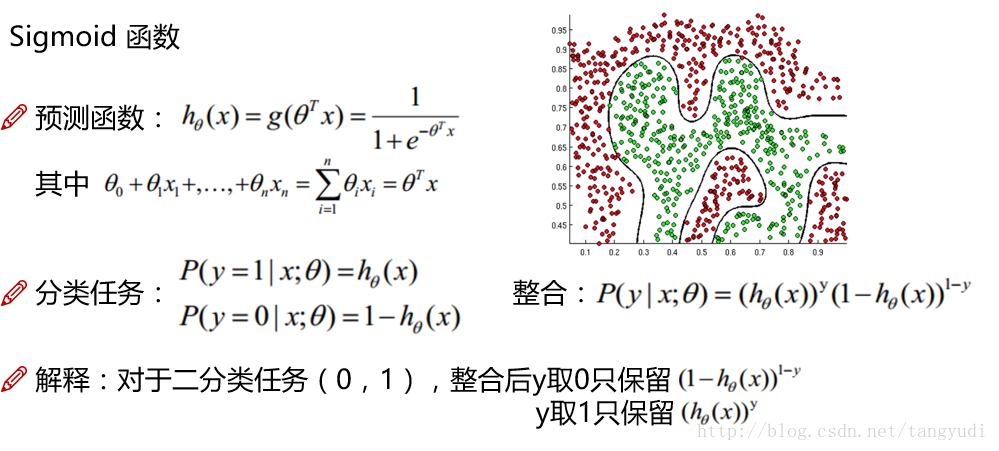
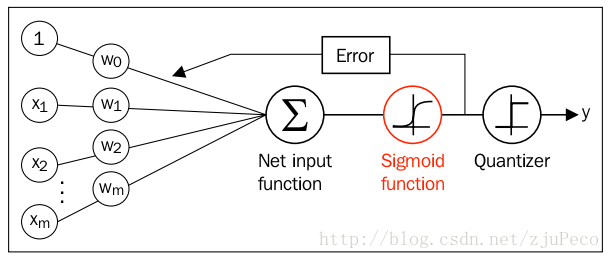
1.2、逻辑回归的损失函数
逻辑回归的损失是它的极大似然函数

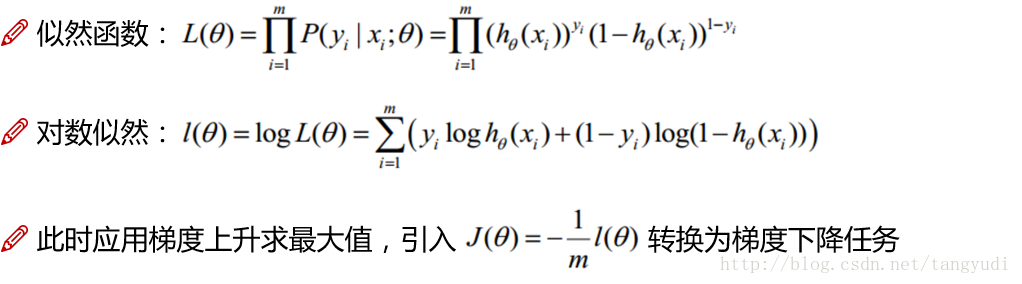
1.3、逻辑回归函数的求解
由于极大似然函数无法直接求解，将其转化为对数函数，利用梯度下降法逼近求解。

2、推导过程

对于一般训练集（所有的向量都为行向量）

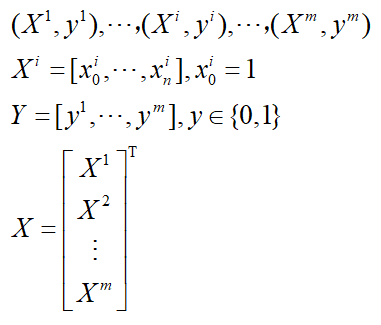
参数系统

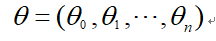
逻辑回归模型：

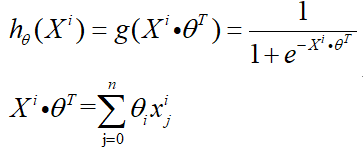
参数求解推导
逻辑回归是用于{0,1}二分类问题，并假设满足伯努利分布：

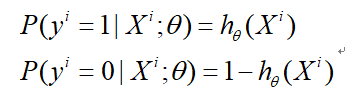
一般形式为：

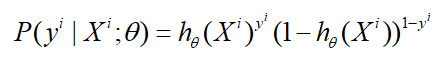
采用最大似然估计求解参数

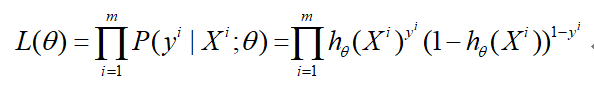
上式两边同时取自然对数

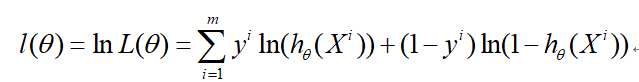
对参数求导并矩阵化：

采用梯度上升发，对参数进行更新：

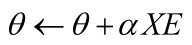
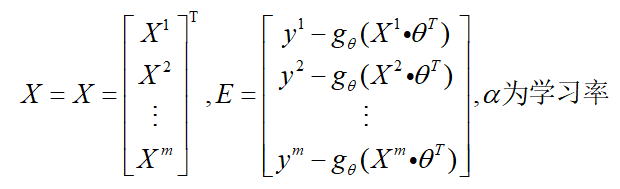
3、代码实现