CNN卷积核反传分析

CNN(卷积神经网络)的误差反传(error back propagation)中有一个非常关键的的步骤就是将某个卷积(Convolve)层的误差传到前一层的池化(Pool)层上，因为在CNN中是2D反传，与传统神经网络中的1D反传有点细节上的不同，下面通过一个简单的例子来详细分解一下这个反传步骤。

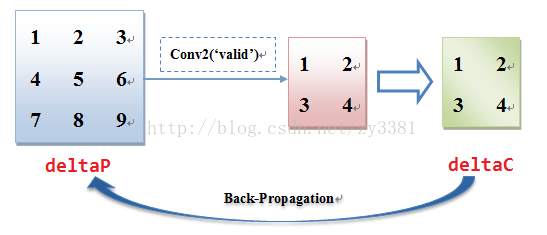
假设在一个CNN网络中，P代表某个池化层，K代表卷积核，C代表卷基层，首先来看一下前向(feed forward)计算，从一个池化层经过与卷积核(Kernel)的运算得到卷积层:

将前向计算的步骤进行分解，可以得到以下公式：

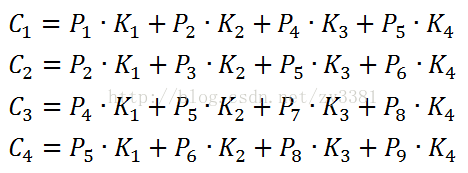
下面根据这个前向计算的步骤来分解出反向传播的步骤：

首先要确定误差传播的目的地，从deltaC到deltaP，所以先从deltaP1开始分析

从前面的前向计算过程中可以找出P1参与了C中哪些元素的计算，并且可以根据对应的前向计算得出反向传播的计算公式：

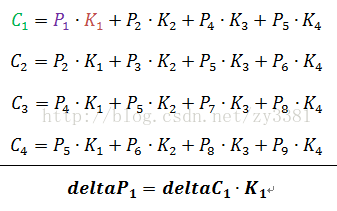
依次类推，还有如下公式：

对于P2

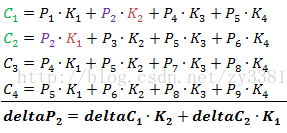
对于P3

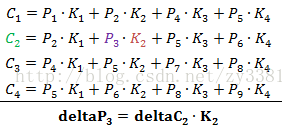
对于P4

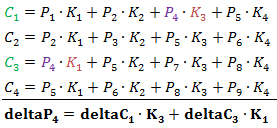
对于P5

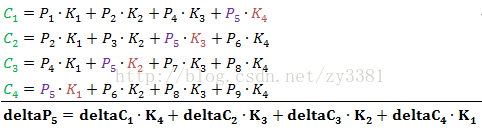
一直可以推到P9

总结这9个反向传播的公式到一起：

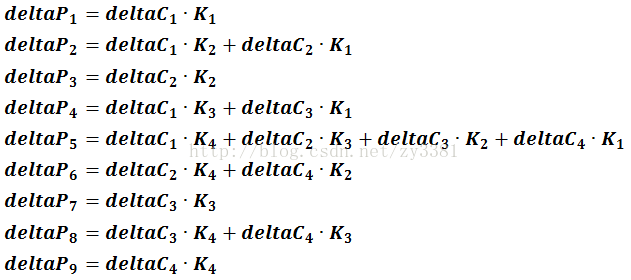
进一步可以发现，这9个公式可以用如下的卷积过程来实现：

至此，从计算的细节上解释了为什么反向传播的时候要把卷积核旋转180°，并采用full的形式来进行卷积运算。

(注：上文所说的“卷积”被认为是一种不会180°旋转第二个因子的的计算过程，实际上matlab中的的conv2(a,b)会自动180°旋转b，换句话说，在matlab中实现这个步骤的时候不用提前旋转，留给conv2函数自行旋转即可)