【POI每日题解 #5】 DWU-Double-row

题目链接 [POI2005]DWU-Double-row

wwwww

之前写了半小时 一卡机 没啦QAQ

简单说一下吧 【吐血ing

这道题长得好二分图啊

所以本能地连边

一种是A边 连可交换的数对

一种是B边 连相同的数字

然后才看题干【Facepalm

发现要求使同一侧没有重复颜色的最小交换次数

然后发现 AB都连上仿佛可做

由于最多两个相同数字

数对也是一对一

每一条长度连起来大于1的路都是A-B-A-B……

不在一个联通快里的点没有相互影响

现在考虑同色同侧

只有这种情况 边的起点和终点才在同一侧

自然想到0-1染色

举个栗子

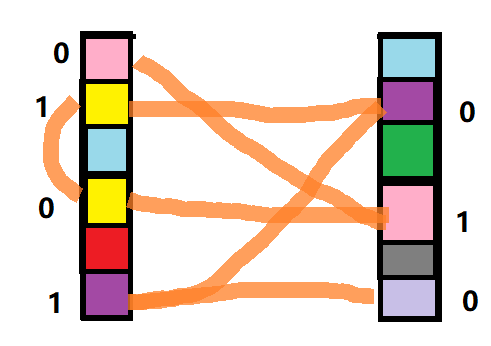
接着我们发现 要使同侧无同色

必须要左侧所有点为同一颜色

因为如果有不同颜色的点

则说明它们之间连接的路上有起点终点同侧的边

也就是同色同侧 不成立

那么怎么改成相反色呢？

每个点连接的1~2条边的另一端点一定是异色 换一下就行了

点的数量没有变 不影响其他点颜色

考虑0，1对称

对于每个联通快 左边1总数和9总数中

取小的那个就是该联通快达到目标状态的最小步数

加起来就好啦

 void dfs(int x, int fa, int col){
     vis[x] = ;
     if(x <= n) cnt[col]++;
     for(int i = head[x]; i != -; i = edge[i].next){
         int vv = edge[i].v;
         if(vis[vv]) continue;
         dfs(vv, x, col ^ );
     }
 }

染色

 //last[i] 上一个值为i的位置 没有为0
     for(int i = ; i <= (n << ); i++) head[i] = -;
     for(int i = ; i <= n; i++){
         int x; scanf("%d", &x);
         if(last[x]) {add(last[x], i); add(i, last[x]);}
         else last[x] = i;
     }
     for(int i = ; i <= n; i++){
         int x; scanf("%d", &x);
         add(i, i + n); add(i + n, i);
         if(last[x]) {add(last[x], i + n); add(i + n, last[x]);}
         else last[x] = i + n;
     }

建边