最小生成树 链式前向星 Prim&Kruskal

Prim：

Prim的思想是将任意节点作为根，再找出与之相邻的所有边（用一遍循环即可），再将新节点更新并以此节点作为根继续搜，维护一个数组：dis，作用为已用点到未用点的最短距离。

证明：Prim算法之所以是正确的，主要基于一个判断：对于任意一个顶点v，连接到该顶点的所有边中的一条最短边(v, vj)必然属于最小生成树（即任意一个属于最小生成树的连通子图，从外部连接到该连通子图的所有边中的一条最短边必然属于最小生成树）

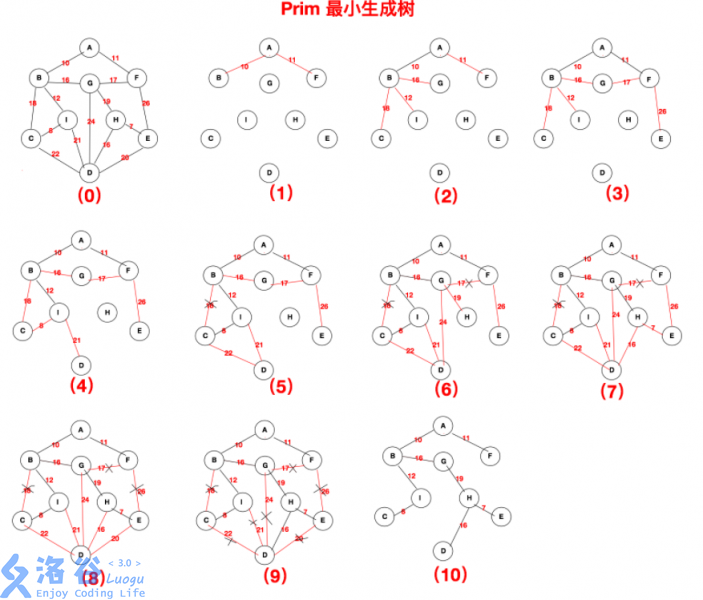
具体算法流程图解如下：

#include <bits/stdc++.h>
typedef long long ll;
using namespace std;
const int mod = 510000;
int he[mod], dis[mod], vis[mod], cns, cnt, n, m, sum;
typedef pair<int, int> PII;
priority_queue<PII, vector<PII>, greater<PII>> q;
struct eage
{
    int a, w, next;
} e[mod << 1];
////链式前向星加边
void add(int x, int a, int w)
{
    e[++cnt].a = a;
    e[cnt].w = w;
    e[cnt].next = he[x];
    he[x] = cnt;
}
void solve1()
{
    q.push({0, 1});
    while (!q.empty() && cns < n)
    {
        int d = q.top().first, a = q.top().second;
        q.pop();
        if (vis[a] == 1)
            continue;
        cns++;
        sum += d;
        vis[a] = 1;
        for (int j = he[a]; j != -1; j = e[j].next)
        {
            if (e[j].w < dis[e[j].a])//判断该点石否走过，未走过则加入优先队列
            {
                dis[e[j].a] = e[j].w;
                q.push({e[j].w, e[j].a});
            }
        }
    }
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    memset(he, -1, sizeof(he));
    memset(dis, 127, sizeof(dis));
    cin >> n >> m;
    for (int i = 1; i <= m; i++)
    {
        int a, b, w;
        cin >> a >> b >> w;
        add(a, b, w);
        add(b, a, w);
    }
    solve1();
    if (cns == n)
        cout << sum;
    else
        cout << "orz";
    return 0;
}