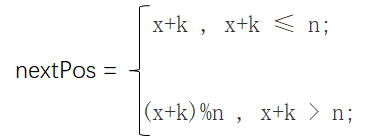UVA 133“The Dole Queue”(循环报数处理技巧)
•参考资料
[1]:紫书P82
•题意(by紫书)
按照被选中的次序输出这 n 个人的编号;
如果A和B选中的是同一个人,输出一个这个人的编号;
输出格式:输出的每个编号占3个字节,不够3个字节在前面用空格补;
•循环报数处理技巧
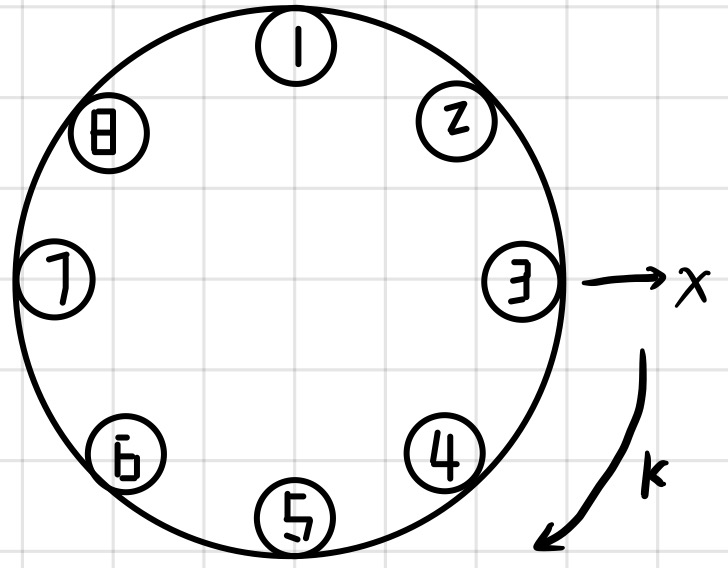
n个人按照逆时针顺序编号1~n;
给你一个整数 k 和 cur;
cur表示从这 n 个人中任意选取的一个编号;
k > 0 : 找 cur 左手边的第 k 个人的编号;
k < 0 : 找 cur 右手边的第 k 个人的编号;
循环报数问题,需要处理的边界问题是:
编号 1 的左手边的人的编号为 n;
编号 n 的右手边的人的编号为 1;
之前常用的处理的方式为,循环处理,如果 cur 从编号 n 来到编号 n+1,特判,令其等于 1;
反之,如果 cur 从编号 1 来到编号 0,特判,令其等于 n;
下面说下一我从紫书上学到的技巧;
1 pos = (cur + k - 1 + n)%n + 1;
pos : 从cur编号顺时针或逆时针找到的第k个人的编号
k : k > ,找cur右手边的第k个人的编号,反之找cur左手边的第k个人的编号;while(~scanf("%d%d%d",&n,&cur,&k))
{
k=k%n;
int pos=(cur+k-1+n)%n+1;
cout<<pos<<endl;
}•我的理解
n个人顺时针围城一圈,从 x 位置开始,顺时针找其左(或逆时针找其右)手边的第 k 个人(-n < k < n , k > 0 顺时针找, k < 0 逆时针找);
假设 k > 0 ,那么第 k 个人的编号为:
合并这两个式子就是
nextPos = (x+k-1+n)%n+1;
简单证明这个式子得正确性:
①如果 x+k ≤ n,那么 (x+k-1+n)%n+1 = x+k;
②如果 x+k > n:
1)x+k = n+1 : (x+k-1+n)%n+1 = 1;
2)x+k > n+1 : (x+k-1+n)%n 就是目的编号的前一个编号,+1就等于目的编号;
那如果 k < 0 呢?
假设找 x 左手边的第 y 个人的编号 = 找 x 右手边的第 k 个人的编号;
那么 |k| + y = n,也就是 y = n-|k|;
带入上式得:
nextPos = (x+n-|k|-1+n)%n+1;
即 nextPos = (x-|k|-1+n)%n+1;
综上,不论 k 是大于0还是小于0,nextPos = (x+k-1+n)%n+1;
•Code
#include<bits/stdc++.h>
using namespace std;
#define memF(a,b,n) for(int i=0;i <= n;a[i++]=b); int n,k,m;
bool vis[]; int Go(int cur,int d,int x)
{
/**
d=1:逆时针找第x个人
d=-1:顺时针找第x个人
当前的cur肯定是不满足条件的位置
所以初始 a=n,b=1
之后,a,b的值就是上一次出队的编号
*/
while(x--)
{
do
{
cur=(cur+d-+n)%n+;
}while(vis[cur]);
}
return cur;
}
void Solve()
{
memF(vis,false,n); int a=n,b=;
int left=n;
while(left--)
{
a=Go(a,,k);
b=Go(b,-,m); vis[a]=true;
vis[b]=true; printf("%3d",a);
if(b != a)
{
left--;
printf("%3d",b);
}
if(left)
printf(",");
}
printf("\n");
}
int main()
{
while(~scanf("%d%d%d",&n,&k,&m) && n+k+m)
Solve(); return ;
}
UVA 133“The Dole Queue”(循环报数处理技巧)的更多相关文章
- UVA 133 The Dole Queue
The Dole Queue 题解: 这里写一个走多少步,返回位置的函数真的很重要,并且,把顺时针和逆时针写到了一起,也真的很厉害,需要学习 代码: #include<stdio.h> # ...
- uva - 133 The Dole Queue(成环状态下的循环走步方法)
类型:循环走步 #include <iostream> #include <sstream> #include <cstdio> #include <cstr ...
- UVA 133 The Dole Queue(报数问题)
题意:一个长度为N的循环队列,一个人从1号开始逆时针开始数数,第K个出列,一个人从第N个人开始顺时针数数,第M个出列,选到的两个人要同时出列(以不影响另一个人数数),选到同一个人就那个人出列. 思路: ...
- uva 133 The Dole Queue 双向约瑟夫环 模拟实现
双向约瑟夫环. 数据规模只有20,模拟掉了.(其实公式我还是不太会推,有空得看看) 值得注意的是两个方向找值不是找到一个去掉一个,而是找到后同时去掉. 还有输出也很坑爹! 在这里不得不抱怨下Uva的o ...
- uva 133(The Dole Queue UVA - 133)
一道比较难想的模拟题,用了队列等东西,发现还是挺难做的,索性直接看了刘汝佳的代码,发现还是刘汝佳厉害! 代码本身难度并不是很大,主要还是p=(p+n+d-1)%n+1;这一句有些难度,实际上经过自己的 ...
- uvaoj 133 - The Dole Queue(逻辑,环形队列数数)
https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem& ...
- UVa133.The Dole Queue
题目链接:http://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem& ...
- The Dole Queue UVA - 133
In a serious attempt to downsize (reduce) the dole queue, The New National Green Labour Rhinoceros ...
- The Dole Queue
The Dole Queue Time Limit:3000MS Memory Limit:0KB 64bit IO Format:%lld & %llu Submit cid ...
随机推荐
- bash shell命令与监测的那点事(二)
bash shell命令与监测的那点事之top 上次我们说到了ps命令,ps命令虽然在收集运行在系统上的进程信息很有用,但是也有不足之处,ps命令只能显示某个特定时间点的信息,如果你想观察频繁换进换出 ...
- 【Rotate List】cpp
题目: Given a list, rotate the list to the right by k places, where k is non-negative. For example:Giv ...
- 最好用的远程连接工具TeamviWer13安装教程(Win10环境)
1.Teamviwer官网:https://www.teamviewer.com/zhCN/ 2.下载链接:https://dl.tvcdn.de/download/TeamViewer_Setup. ...
- 11 JVM 垃圾回收(上)
引用计数法和可达性分析 垃圾回收,就是将已经分配出去的,但却不在使用的内存回收回来,以便再次分配.在 Java 虚拟机语境下,垃圾指的是死亡的对象所占据的堆空间.下面就总结一下如何如何辨别一个对象是否 ...
- sqlserver2008透明书库加密
/*Title:TDE加密Author:浪客Environment:Windows Server 2008 Enterprise + SQL Server 2008 EnterpriseDescrip ...
- 【转载】zookeeper使用和原理探究(一)
最近开始看到一些公司在使用zookeeper,本身对此了解的很少,这里看到一篇非常好的文章,因此转载 原贴地址:http://www.blogjava.net/BucketLi/archive/201 ...
- jQuery ajax使用$(this).parent()无效解决方法
div=$(this).parent(); //先获取父级元素 div.remove(); //再删除 $(".delStu").click(function () { ...
- C#的一些基本问题
静态类和静态变量静态类的定义:static class 类名 静态方法和变量必须使用类名来引用,而不能使用实例化后的对象,因为,静态变量不属于任何实例,而是共有的. 非静态类里面既可以定义静态方法也可 ...
- hihoCoder 1133 二分·二分查找之k小数(TOP K算法)
#1133 : 二分·二分查找之k小数 时间限制:10000ms 单点时限:1000ms 内存限制:256MB 描述 在上一回里我们知道Nettle在玩<艦これ>,Nettle的镇守府有很 ...
- BZOJ3720 Gty的妹子树 【树分块】
题目 我曾在弦歌之中听过你, 檀板声碎,半出折子戏. 舞榭歌台被风吹去, 岁月深处尚有余音一缕-- Gty神(xian)犇(chong)从来不缺妹子-- 他来到了一棵妹子树下,发现每个妹子有一个美丽度 ...