可持久化treap（FHQ treap）

FHQ treap 的整理

treap = tree + heap，即同时满足二叉搜索树和堆的性质。

为了使树尽可能的保证两边的大小平衡，所以有一个key值，使他满足堆得性质，来维护树的平衡，key值是随机的。

treap有一般平衡树的功能，前驱、后继、第k大、查询排名、插入、删除。也比较好写

但是对于区间上的问题是不能做的，例如

• 区间增减
• 区间求最值
• 区间反转（倒序）
• 区间移动（把一段剪切、粘贴）

（splay是可以做的）

但是有一种神奇的数据结构，即可以满足treap的功能，也可以区间上进行操作——FHQ treap

FHQ treap 只有两个基本操作，所以代码量也小的多。

split

分离，讲一个treap分成两个treap。

有两种分离的类型，一个是按照权值val分，小于等于k的分成一个，大于的一个。另一种是取出区间上的前k个数。

权值：

对于一颗treap，小于等于k的点是存在于一颗子树中的，但是这颗子树可能有大于k的，所以在拆分时，是要重建这棵树的。

 void Split(int now,int k,int &x,int &y) {
     if (!now) x = y = ;
     else {
         if (val[now] <= k)
             x = now,Split(ch[now][],k,ch[now][],y);
         else
             y = now,Split(ch[now][],k,x,ch[now][]);
         pushup(now);
     }
 }

代码非常奇妙，它引用了两个值，x，y，这两个值就是重建的最重要的两个变量，一定要有取地址符。

x引用的是一个小于等于k的节点（假设是a）的右儿子，y引用的是一个大于k的节点左儿子。

这里a是小于等于k的，它的左子树也是小于等于k的，但是右儿子却不一定是小于k的，所以这里取出它的右儿子，当遇到第一个小于k的节点是，让它成为a的右儿子。

如下图，k=6，那么a是小于6的，往右走，发现右儿子是大于6的，所以a的右儿子是要改变的，接下来往左走的过程中，将a的右儿子指向权值为6的点即可。

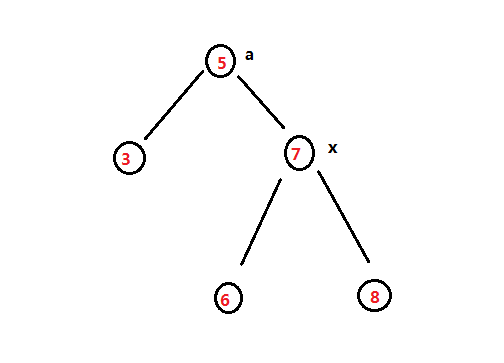
重建的过程：如果当前点now的值小于k那么，他的左边一定都是小于k的，所以往右走。

复杂度 $O(logn)$

区间上前k个数

 void Split(int now,int k,int &x,int &y) {
     if (!now) x=y=;
     else {
         if (k <= siz[ch[now][]])
             y = now,Split(ch[now][],k,x,ch[now][]);
         else
             x = now,Split(ch[now][],k-siz[ch[now][]]-,ch[now][],y);
         pushup(now);
     }
 }

原理是一样的，不详细说了。

复杂度，$O(logn)$

merge

合并两颗子树，保证第一颗树的所有点的权值都小于第二颗子树的所有节点。

那么重建只要满足堆的性质就好了。

还是有两个变量x，y，

 int Merge(int x,int y) {
     if (!x || !y) return x + y;
     if (key[x] < key[y]) {
         ch[x][] = Merge(ch[x][],y);
         pushup(x); return x;
     }
     else {
         ch[y][] = Merge(x,ch[y][]);
         pushup(y); return y;
     }
 }

这里会发现，当x树的key小时，只将x的左半边加入到重建的树中，y子树小时，只将它的右半边加入到子树中。为了满足treap的性质。

复杂度 $O(logn)$

两个基本操作就完成了。

insert

插入一个权值为k的数。

过程：把treap分成两个，小于等于k的，大于k的，把x和两个子树合并即可

Split(Root,k,x,y);
Root = Merge(Merge(x,makenode(k)),y);

delete

删除一个权值为k的数。

过程：先分成小于等于k的 a 和大于k的 b ，之后将x分成小于等于k-1的 c 和大于k-1的 d ，d就是k，所以将d的两个儿子合并起来，然后与c，b合并即可；

Split(Root,k,x,y);
Split(x,k-,x,z);
z = Merge(ch[z][],ch[z][]);
Root = Merge(Merge(x,z),y);

k的排名

求k的排名

过程：分成小于等于k-1的 x ，和大于k-1 的 y 两个子树，子树x的大小就是k的排名。

Split(Root,k-,x,y);
printf("%d\n",siz[x]+);
Root = Merge(x,y);

第k个数

求第k个数

过程：和splay，treap一样的求法；

inline int getkth(int p,int k) {
    while (true) {
        if (k == siz[ch[p][]] + ) return p;
        if (ch[p][] && k <= siz[ch[p][]]) p = ch[p][];
        else k-= ((ch[p][] ? siz[ch[p][]] : ) + ),p = ch[p][];
    }
}

前驱

求k的排名

过程：分成小于等于k-1的 x ，和大于k-1 的 y 两个子树，子树x中最大的数就是x的前驱。

Split(Root,k-,x,y);
printf("%d\n",val[getkth(x,siz[x])]);
Root = Merge(x,y);

后继

求k的排名

过程：分成小于等于k的 x ，和大于k 的 y 两个子树，子树y中最小的数就是x的前驱。

Split(Root,k,x,y);
printf("%d\n",val[getkth(y,)]);
Root = Merge(x,y);

FHQtreap的基本操作就是这些了

例题

普通平衡树

 #include<cstdio>
 #include<algorithm>

 using namespace std;

 const int N = ;
 int ch[N][],siz[N],key[N],val[N];
 int tn,Root;

 inline char nc() {
     static char buf[],*p1 = buf,*p2 = buf;
     return p1==p2&&(p2=(p1=buf)+fread(buf,,,stdin),p1==p2) ? EOF : *p1++;
 }
 inline int read() {
     int x = ,f = ;char ch = getchar();
     for (; ch<''||ch>''; ch = getchar())
         if (ch=='-') f = -;
     for (; ch>=''&&ch<=''; ch = getchar())
         x = x*+ch-'';
     return x * f;
 }
 inline void pushup(int x) {
     siz[x] = siz[ch[x][]] + siz[ch[x][]] + ;
 }
 inline int makenode(int x) {
     ++tn;val[tn] = x;siz[tn] = ;key[tn] = rand();return tn;
 }

 int Merge(int x,int y) {
     if (!x || !y) return x + y;
     if (key[x] < key[y]) {
         ch[x][] = Merge(ch[x][],y);
         pushup(x); return x;
     }
     else {
         ch[y][] = Merge(x,ch[y][]);
         pushup(y); return y;
     }
 }
 void Split(int now,int k,int &x,int &y) {
     if (!now) x = y = ;
     else {
         if (val[now] <= k)
             x = now,Split(ch[now][],k,ch[now][],y);
         else
             y = now,Split(ch[now][],k,x,ch[now][]);
         pushup(now);
     }
 }
 inline int getkth(int p,int k) {
     while (true) {
         if (k == siz[ch[p][]] + ) return p;
         if (ch[p][] && k <= siz[ch[p][]]) p = ch[p][];
         else k-= ((ch[p][] ? siz[ch[p][]] : ) + ),p = ch[p][];
     }
 }
 int main() {
     int x,y,z,opt,k,n = read();
     while (n--) {
         opt = read(),k = read();
         if (opt==) {
             Split(Root,k,x,y);
             Root = Merge(Merge(x,makenode(k)),y);
         }
         else if (opt==) {
             Split(Root,k,x,y);
             Split(x,k-,x,z);
             z = Merge(ch[z][],ch[z][]);
             Root = Merge(Merge(x,z),y);
         }
         else if (opt==) {
             Split(Root,k-,x,y);
             printf("%d\n",siz[x]+);
             Root = Merge(x,y);
         }
         else if (opt==)
             printf("%d\n",val[getkth(Root,k)]);
         else if (opt==) {
             Split(Root,k-,x,y);
             printf("%d\n",val[getkth(x,siz[x])]);
             Root = Merge(x,y);
         }
         else {
             Split(Root,k,x,y);
             printf("%d\n",val[getkth(y,)]);
             Root = Merge(x,y);
         }
     }
     return ;
 }

文艺平衡树

 #include<cstdio>
 #include<algorithm>

 using namespace std;

 const int N = ;

 int ch[N][],tag[N],val[N],siz[N],key[N];
 int tn,Root,n,m;

 inline char nc() {
     static char buf[],*p1 = buf,*p2 = buf;
     return p1==p2&&(p2=(p1=buf)+fread(buf,,,stdin),p1==p2) ? EOF : *p1++;
 }
 inline int read() {
     int x = ,f = ;char ch = nc();
     for (; ch<''||ch>''; ch = nc())
         if (ch=='-') f = -;
     for (; ch>=''&&ch<=''; ch = nc())
         x = x*+ch-'';
     return x * f;
 }
 inline void pushup(int x) {
     siz[x] = siz[ch[x][]] + siz[ch[x][]] + ;
 }
 inline void pushdown(int x) {
     if (x && tag[x]) {
         tag[x] ^= ;
         swap(ch[x][],ch[x][]);
         if (ch[x][]) tag[ch[x][]] ^= ;
         if (ch[x][]) tag[ch[x][]] ^= ;
     }
 }
 inline int makenode(int x) {
     ++tn;siz[tn] = ;val[tn] = x;key[tn] = rand();return tn;
 }
 int merge(int x,int y) {
     if (!x || !y) return x + y;
     pushdown(x);pushdown(y);
     if (key[x] < key[y]) {
         ch[x][] = merge(ch[x][],y);
         pushup(x);return x;
     }
     else {
         ch[y][] = merge(x,ch[y][]);
         pushup(y);return y;
     }
 }
 void split(int now,int k,int &x,int &y) {
     if (!now) x = y = ;
     else {
         pushdown(now);
         if (k<=siz[ch[now][]])
             y = now,split(ch[now][],k,x,ch[now][]);
         else
             x = now,split(ch[now][],k-siz[ch[now][]]-,ch[now][],y);
         pushup(now);
     }
 }
 inline void rever(int l,int r) {
     int a,b,c,d;
     split(Root,r,a,b);
     split(a,l-,c,d);
     tag[d] ^= ;
     Root = merge(merge(c,d),b);
 }
 void print(int x) {
     if (!x) return ;
     pushdown(x);
     print(ch[x][]);
     printf("%d ",val[x]);
     print(ch[x][]);
 }
 int main() {
     n = read(),m = read();
     for (int i=; i<=n; ++i) {
         Root = merge(Root,makenode(i));
     }
     while (m--) {
         int a = read(),b = read();
         rever(a,b);
     }
     print(Root);
     return ;
 } 

=========