【BZOJ1150】[CTSC2007]数据备份Backup 双向链表+堆（模拟费用流）

【BZOJ1150】[CTSC2007]数据备份Backup

Description

　　你在一家 IT 公司为大型写字楼或办公楼（offices）的计算机数据做备份。然而数据备份的工作是枯燥乏味的，因此你想设计一个系统让不同的办公楼彼此之间互相备份，而你则坐在家中尽享计算机游戏的乐趣。已知办公楼都位于同一条街上。你决定给这些办公楼配对（两个一组）。每一对办公楼可以通过在这两个建筑物之间铺设网络电缆使得它们可以互相备份。然而，网络电缆的费用很高。当地电信公司仅能为你提供 K 条网络电缆，这意味着你仅能为 K 对办公楼（或总计2K个办公楼）安排备份。任一个办公楼都属于唯一的配对组（换句话说，这 2K 个办公楼一定是相异的）。此外，电信公司需按网络电缆的长度（公里数）收费。因而，你需要选择这 K 对办公楼使得电缆的总长度尽可能短。换句话说，你需要选择这 K 对办公楼，使得每一对办公楼之间的距离之和（总距离）尽可能小。下面给出一个示例，假定你有 5 个客户，其办公楼都在一条街上，如下图所示。这 5 个办公楼分别位于距离大街起点 1km, 3km, 4km, 6km 和 12km 处。电信公司仅为你提供 K=2 条电缆。

　　上例中最好的配对方案是将第 1 个和第 2 个办公楼相连，第 3 个和第 4 个办公楼相连。这样可按要求使用K=2 条电缆。第 1 条电缆的长度是 3km-1km=2km ，第 2 条电缆的长度是 6km-4km=2km。这种配对方案需要总长4km 的网络电缆，满足距离之和最小的要求。

Input

　　输入的第一行包含整数n和k，其中n（2 ≤ n ≤100 000）表示办公楼的数目，k（1≤ k≤ n/2）表示可利用的网络电缆的数目。接下来的n行每行仅包含一个整数（0≤ s ≤1000 000 000）, 表示每个办公楼到大街起点处的距离。这些整数将按照从小到大的顺序依次出现。

Output

　　输出应由一个正整数组成，给出将2K个相异的办公楼连成k对所需的网络电缆的最小总长度。

Sample Input

5 2
1
3
4
6
12

Sample Output

4

题解：如果你略懂费用流建模的话，相信这题你一定知道费用流的建法，本题的费用流模型大概长这样：

为了限流，将源点拆成两个。再将每个办公楼拆成两个，中间边的费用就是二者的距离。

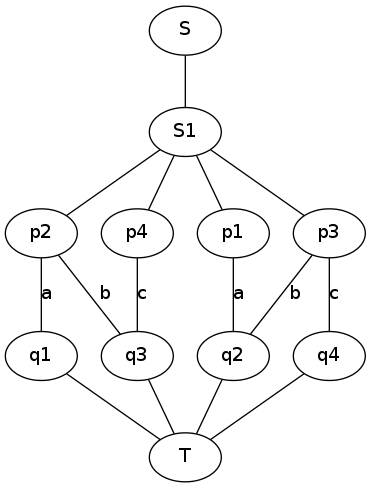
垃圾画图软件。。。这里就自行脑补一下，每一层的顺序都是p1,p2,p3,p4吧。。。

假如k=2，并且b<a<c，那么我们跑费用流的时候就会先走两条费用为b的边，然后图中又会出现两条费用为-b的反向边。然后我们继续流，此时我们发现可以走两条费用为a+c-b的边，然后跑完了，总费用2a+2c。

然后我们想办法模拟这个过程，先求出所有相邻的办公楼之间的距离，每次用优先队列选出长度最小的那个间隔，然后将那个间隔的前一个和后一个间隔删掉，将当前间隔的长度改为(前一个的长度+后一个的长度-这个的长度)。删除的操作可以用双向链表实现。

#include <cstdio>
#include <cstring>
#include <iostream>
#include <queue>
#include <utility>
#define mp(A,B) make_pair(A,B)
using namespace std;
const int maxn=100010;
const int inf=500000000;
struct node
{
	int pre,next,val,del;
}p[100010];
typedef pair<int,int> pii;
priority_queue<pii> pq;
int n,m,ans;
int v[maxn];
int rd()
{
	int ret=0,f=1;	char gc=getchar();
	while(gc<'0'||gc>'9')	{if(gc=='-')f=-f;	gc=getchar();}
	while(gc>='0'&&gc<='9')	ret=ret*10+gc-'0',gc=getchar();
	return ret*f;
}
int main()
{
	n=rd(),m=rd();
	int i,a;
	for(i=1;i<=n;i++)	v[i]=rd();
	for(i=1;i<n;i++)
	{
		p[i].val=v[i+1]-v[i];
		p[i].pre=i-1,p[i].next=(i+1==n)?0:i+1;
		pq.push(mp(-p[i].val,i));
	}
	p[0].val=inf;
	pii x;
	for(i=1;i<=m;i++)
	{
		do
		{
			x=pq.top(),pq.pop();
		}while(p[x.second].del);
		ans+=-x.first,a=x.second,p[a].val=p[p[a].pre].val+p[p[a].next].val-p[a].val;
		if(p[a].pre)
		{
			p[p[a].pre].del=1,p[a].pre=p[p[a].pre].pre;
			if(p[a].pre)	p[p[a].pre].next=a;
		}
		if(p[a].next)
		{
			p[p[a].next].del=1,p[a].next=p[p[a].next].next;
			if(p[a].next)	p[p[a].next].pre=a;
		}
		pq.push(mp(-p[a].val,a));
	}
	printf("%d",ans);
	return 0;
}