无监督学习：Linear Dimension Reduction(线性降维)

一 Unsupervised Learning

把Unsupervised Learning分为两大类：

• 化繁为简：有很多种input，进行抽象化处理，只有input没有output
• 无中生有：随机给一个input，自动画一张图，只有output没有input

二 Clustering

有一大堆image ，把他们分为几大类，给他们贴上标签，将不同的image用相同的 cluster表示。 也面临一个问题，要有多少种cluster呢？ 有两种clustering的方法：

2.1 K-means(K均值)

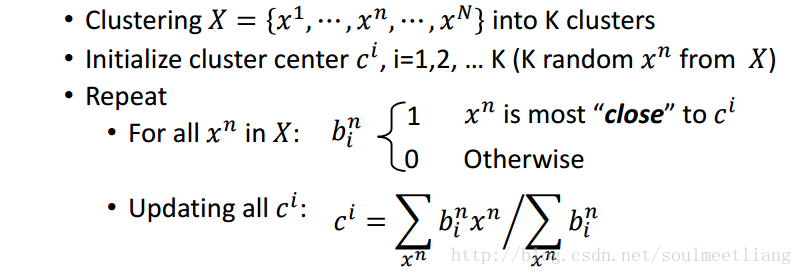
2.2 Hierarchical Agglomerative Clustering (HAC阶层式汇聚分群法)

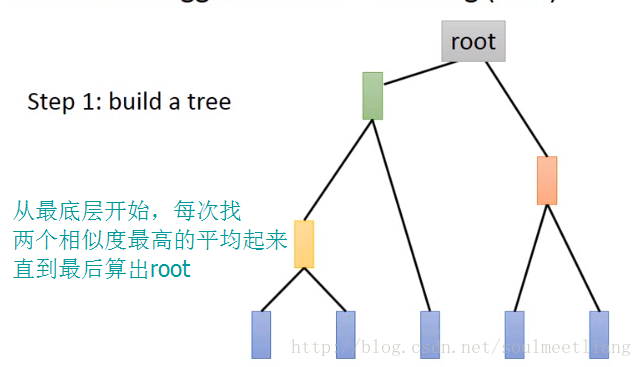
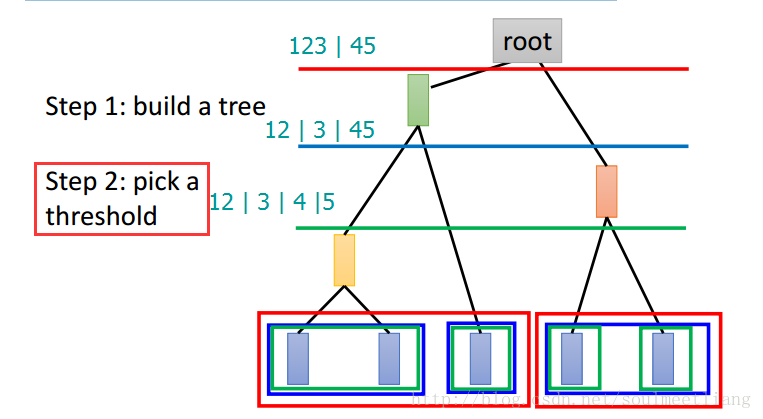
注：如果说K均值算法的问题是不好却确定分为几类，那么HAC的问题在于不知将分类门槛划在哪一层。

三 Distributed Representation（分布式表征）

光做clustering是很卡的，有的个体并不只属于一个大类，所以需要一个vector来表示在各个类中的概率。这样，从一个（高维）图片到一个各个属性概率（低维）就是一个Dimension Reduction。

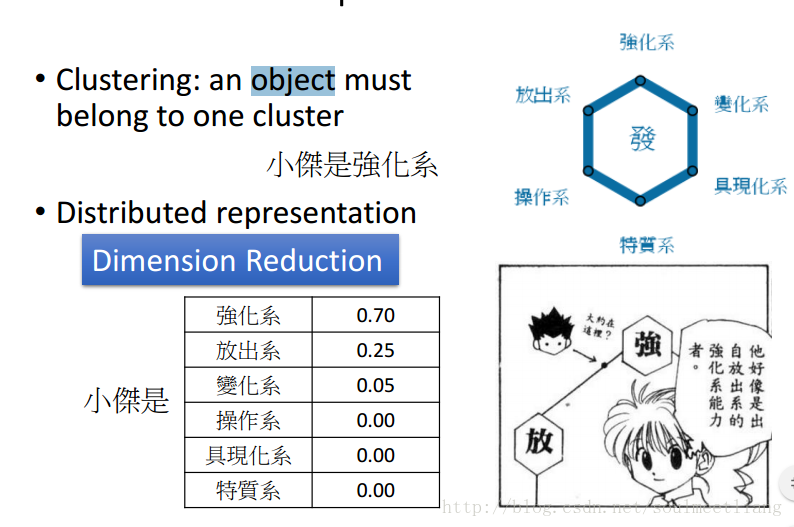
四 Dimension Reduction

为什么说降维是很有用的呢？ 有时候在3D很复杂的图像到2D就被简化了。

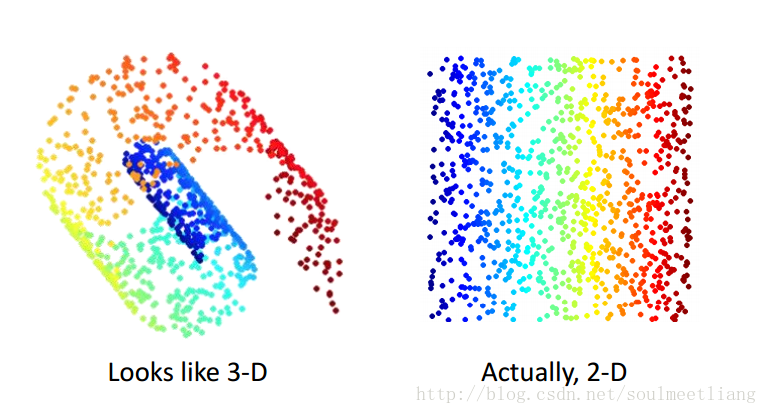
在MNIST训练集中，很多28*28维的向量转成一个image看起来根本不像数字，其中是digit的vector很少，所以或许我们可以用少于28*28维的向量来描述它。 比如下图一堆3，每一个都是28*28维的向量，但是，我们发现，它们仅仅是角度的不同，所以我们可以加上角度值进行降维，来简化表示。

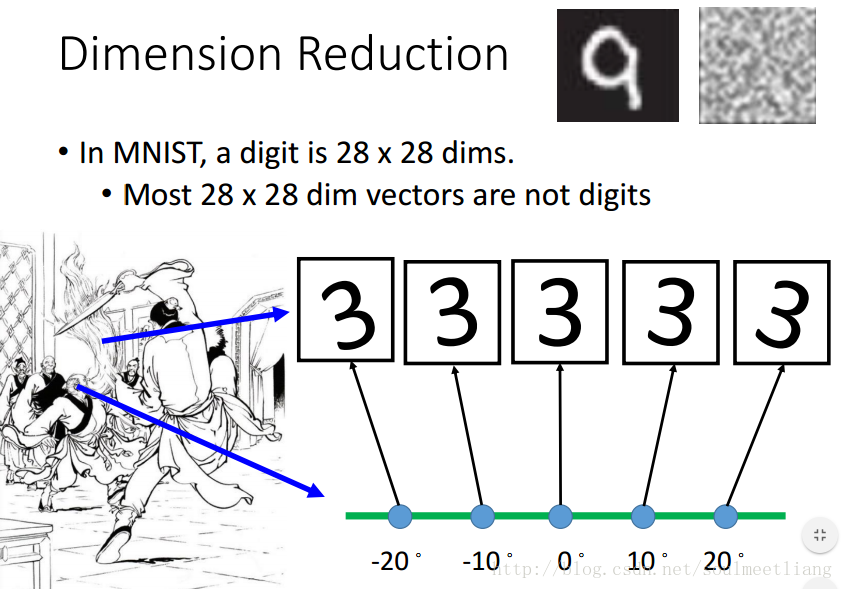
那我们应该怎样做Dimension Reduction呢？ 就是要找一个function。有两个方法：

• Feature selection特征选择：比如在左图二维坐标系中，我们发现X1轴对样本点影响不大，那么就可以把它拿掉。
• PCA 主成分分析： 输出 z=Wx输入，找到这个向量W。

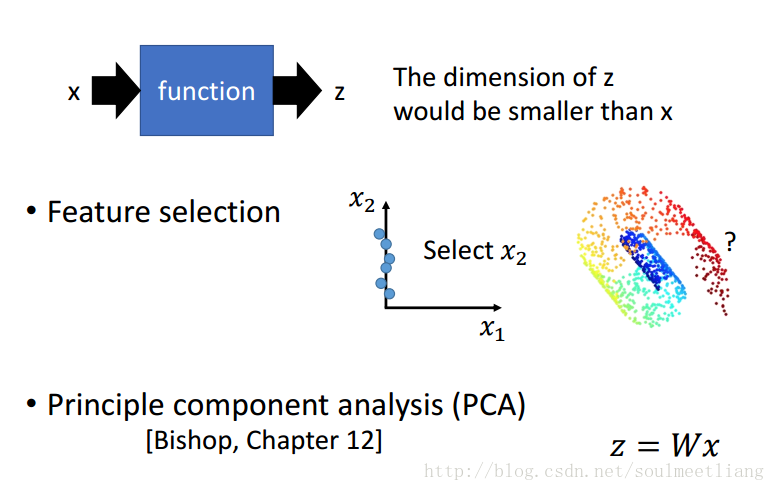
在现实中我们很难确定某个因素是否真的不起作用，所以下边重点介绍一个PCA

4.1 Principle Component Analysis (PCA) 主成分分析

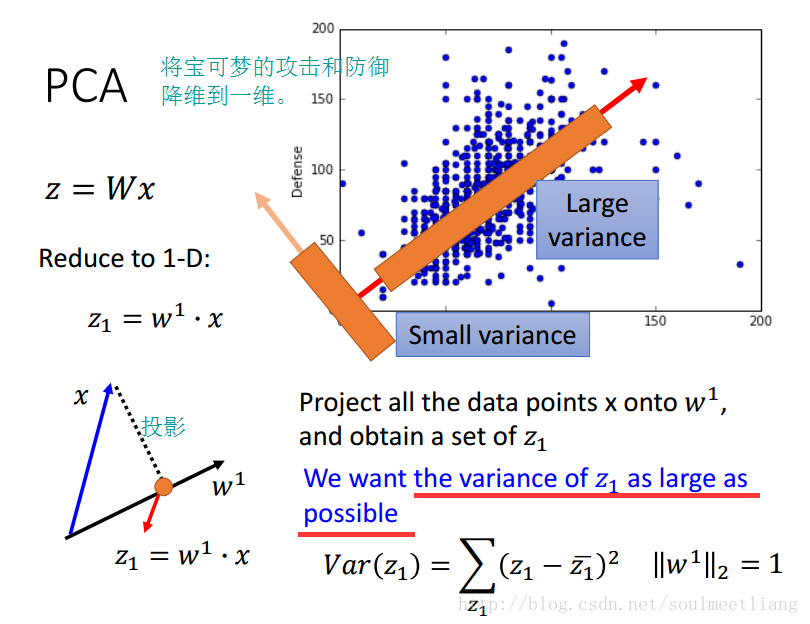
在一维的例子里，我们要找 z1 方差最大的情况，当维度升高到2维，找 z2 方差最大，为了避免与 z1 重复，所以规定 w1 与 w2 垂直。依次方法可进行高维计算。将所有w转置一下，组成一个高维向量，就是我们要找的W。

---

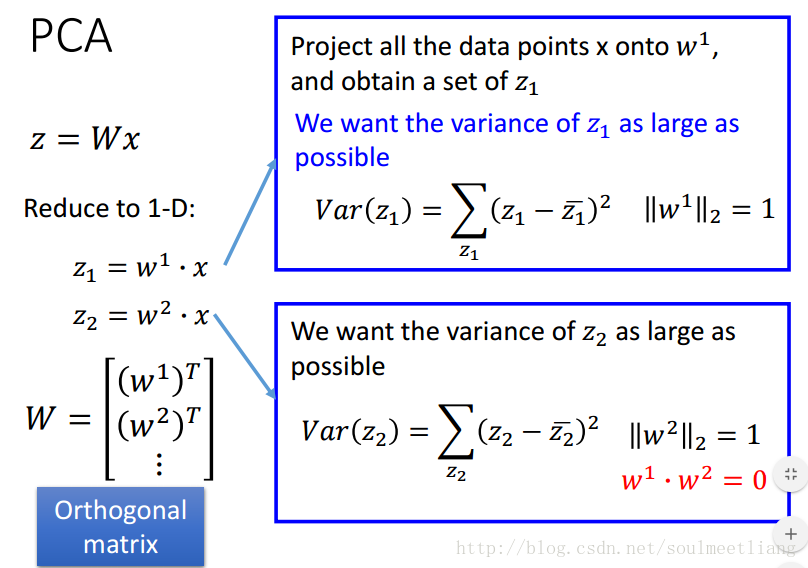
补充一些数学知识（为了求解w）：

---

4.2 PCA - decorrelation

4.3 PCA – Another Point of View

每个手写识别，都是由基础组件构成的，把基础组件加起来，得到一个数字。 对7来说，C1\C2\C3\C4\C5分别为1\0\1\0\1

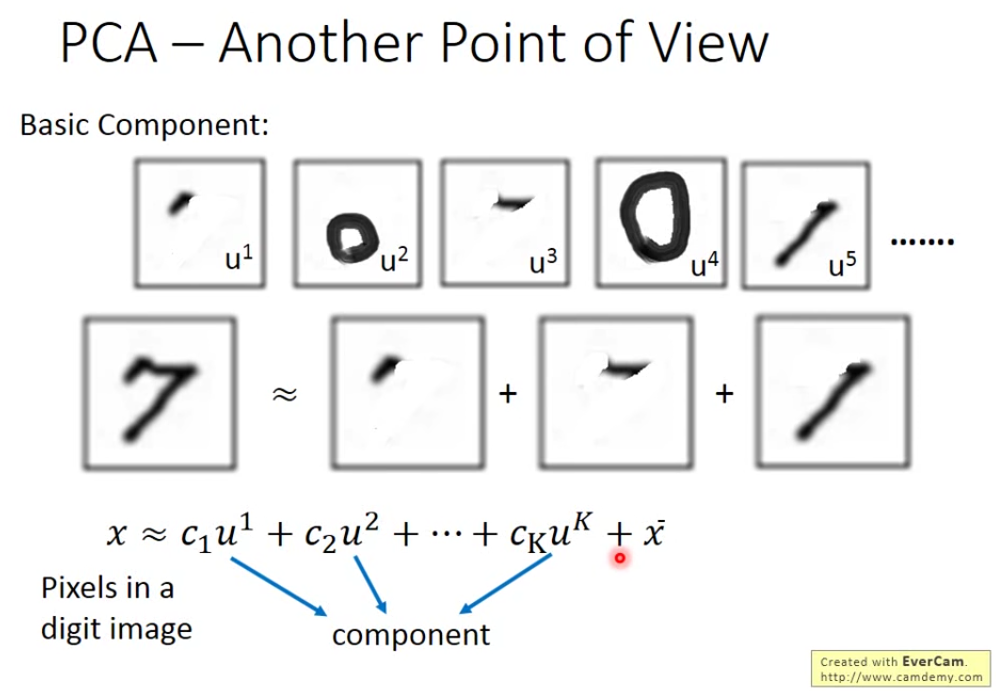
那我们如何找到 u1-uK这K个Vector呢？ 我们要找K个vector使重构误差越小越好。

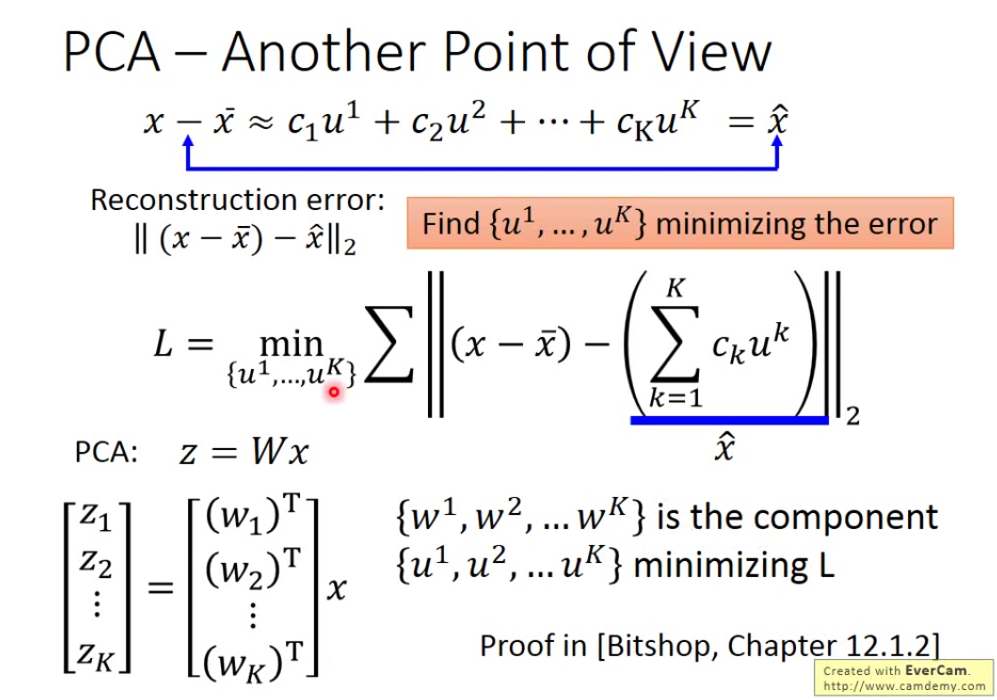
转化为Matrix。

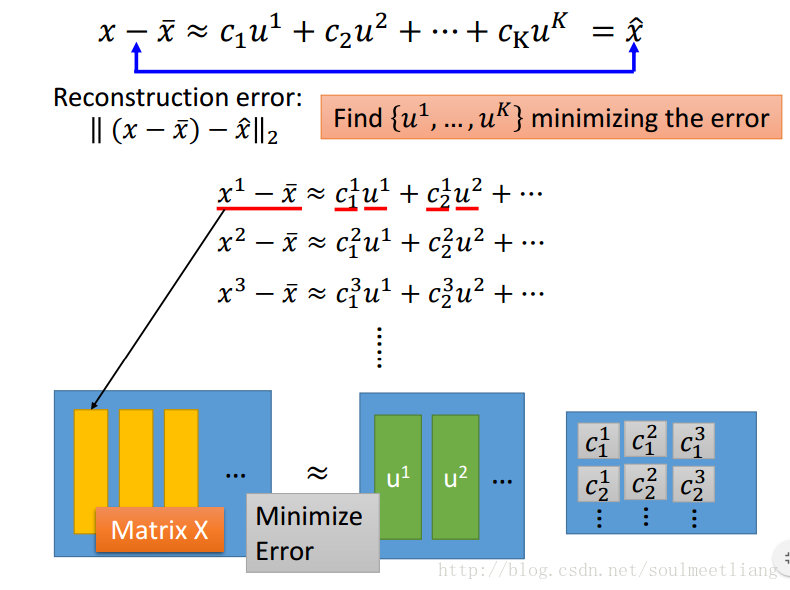
怎么解这个问题呢？SVD方法： matrix X 可以用SVD拆成 matrix U * matrix ∑ * matrix V。

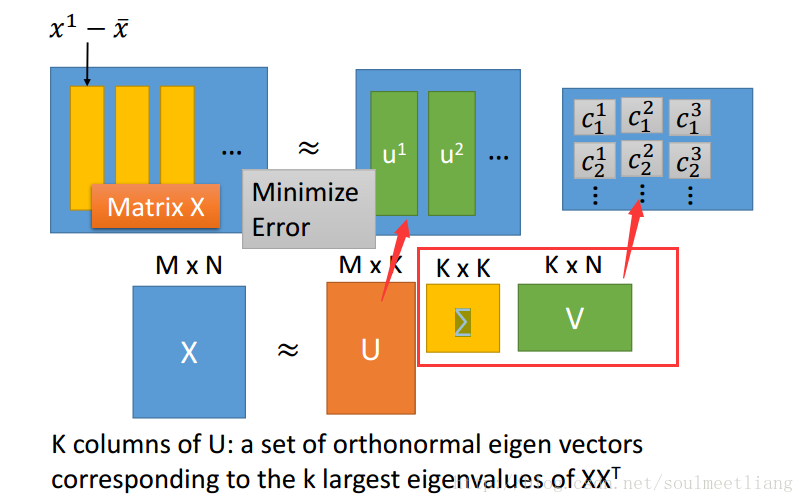
这样w已经通过SVD求出来了，Ck怎么求呢？

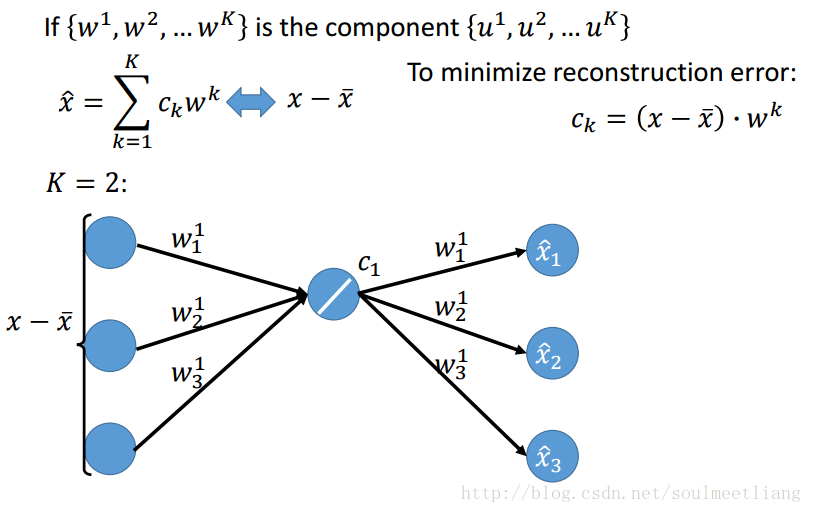
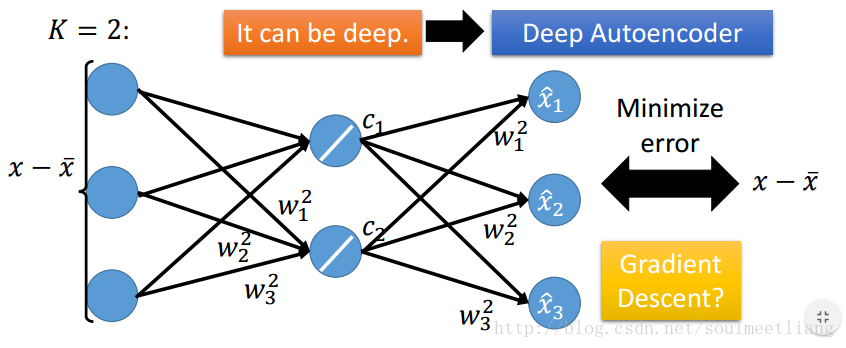
 4.4 Weakness of PCA

参考：

http://speech.ee.ntu.edu.tw/~tlkagk/courses/ML_2016/Lecture/dim%20reduction%20%28v5%29.pdf

https://blog.csdn.net/soulmeetliang/article/details/73309360