Hanoi双塔问题

题目描述:

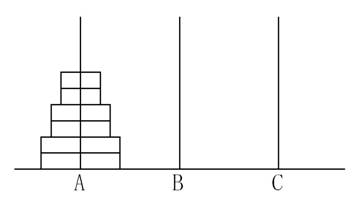
给定A、B、C三根足够长的细柱，在A柱上放有2n个中间有孔的圆盘，共有n个不同的尺寸，每个尺寸都有两个相同的圆盘，注意这两个圆盘是不加区分的（下图为n=3的情形）。现要将这些圆盘移到C柱上，在移动过程中可放在B柱上暂存。要求：

（1）每次只能移动一个圆盘；

（2）A、B、C三根细柱上的圆盘都要保持上小下大的顺序；

任务：设An为2n个圆盘完成上述任务所需的最少移动次数，对于输入的n，输出An。

输入格式:

一个正整数n，表示在A柱上放有2n个圆盘。

输出格式:

包含一个正整数, 为完成上述任务所需的最少移动次数An。

样例输入:

2

样例输出:

6

思路：这题建立递归式就大功告成了，不过要高精。

不多说了，上代码：

#include<cstdio>
#define len 1e4
#define maxn 100
using namespace std;
int ans[maxn];
void multi(){
      int i,last=;
      for(i=;i<=ans[];i++){
      ans[i]=ans[i]*+last;
      last=ans[i]/len,ans[i]%=len;
    }
      if(last)ans[++ans[]]=last;
}
int main(){
  int n,i;
  scanf("%d",&n);
  ans[]=,ans[]=;
  for(i=;i<=n;i++)multi();
  ans[]-=;  printf("%d",ans[ans[]]);
  for(i=ans[]-;i>=;i--)printf("%04d",ans[i]);
  return ;
}