联赛模拟测试22 D. 简单计算

题目描述

分析

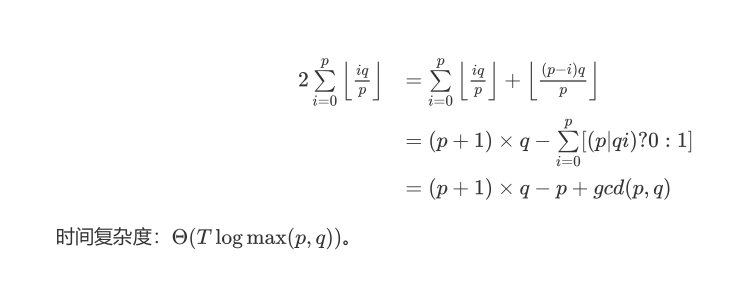
\(\sum_{i=0}^p[(p|qi)?0:1]=\sum_{i=0}^p[(p/gcd(p,q)|qi/gcd(p,q))?0:1]=\sum_{i=0}^p[(p/gcd(p,q)|i)?0:1]=p-p/gcd(p,q)\)

代码

#include<cstdio>
long long t,p,q,ans;
long long gcd(long long aa,long long bb){
	if(bb==0) return aa;
	return gcd(bb,aa%bb);
}
int main(){
	scanf("%lld",&t);
	while(t--){
		ans=0;
		scanf("%lld%lld",&p,&q);
		ans=(p+1)*q-p+gcd(p,q);
		printf("%lld\n",ans/2);
	}
	return 0;
}