Codeforces Global Round 11 C. The Hard Work of Paparazzi（dp/最长上升子序列）

题目链接：https://codeforces.com/contest/1427/problem/C

题意

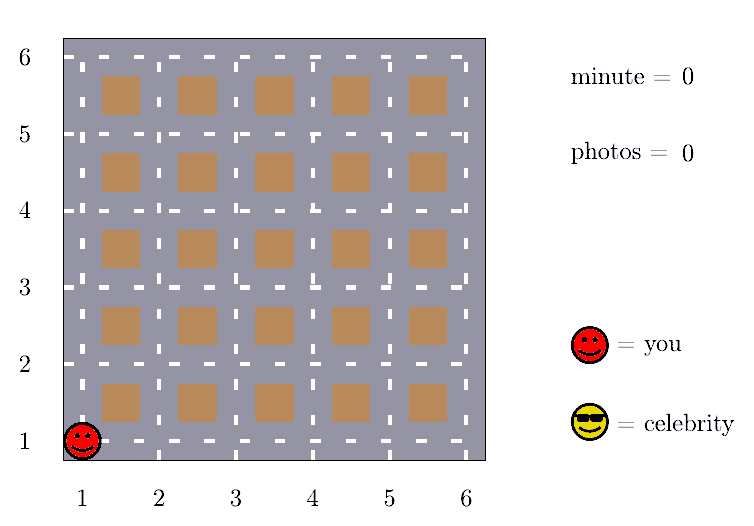
\(r\) 行与 \(r\) 列相交形成了 \(r \times r\) 个点，初始时刻记者位于左下角的 \((1,1)\) 处，接下来给出 \(n\) 个名人的出现时间和位置，出现时间严格递增，问记者最多可以拍到多少名人的照片。

题解

This is a classical dynamic-programming task with a twist.

这是一个有些变化的经典动态规划问题。

与最长上升子序列问题的不同之处的是，本题判断条件由 \(a_j > a_i\) 变为了 \(dis_{ij} \le t_j - t_i\) 以及利用 \(r\) 将 \(O_{(n^2)}\) 优化至了 \(O_{(nr)}\) 。

代码

#include <bits/stdc++.h>
using namespace std;
int main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	int r, n;
	cin >> r >> n;
	//如果 r == 1，此时只有 1 个点
	if (r == 1) {
		cout << n << "\n";
		return 0;
	}
	vector<int> t(n + 1), x(n + 1), y(n + 1);
	t[0] = 0, x[0] = 1, y[0] = 1;
	for (int i = 1; i <= n; i++)
		cin >> t[i] >> x[i] >> y[i];
	vector<int> dp(n + 1, -1e9), mx_dp(n + 1);
	dp[0] = 0; //初始时只有时刻 0 的 (1,1) 可达
	for (int i = 1; i <= n; i++) {
		//继承之前可达的 dp 状态
		for (int j = max(i - 2 * (r - 1), 0); j < i; j++) {
			if (abs(x[i] - x[j]) + abs(y[i] - y[j]) <= t[i] - t[j])
				dp[i] = max(dp[i], dp[j] + 1);
		}
		//如果 i 大于等于最长路径，那么对于 dp[0] ~ dp[i - 2 * (r - 1)] 一定是可达的
		if (i >= 2 * (r - 1)) dp[i] = max(dp[i], mx_dp[i - 2 * (r - 1)] + 1);
		mx_dp[i] = max(dp[i], mx_dp[i - 1]);
	}
	cout << mx_dp[n] << "\n";
	return 0;
}