题解-Infinite Path

题解-Infinite Path

\(\color{#9933cc}{\texttt{Infinite Path}}\)

\(T\) 组测试数据。每次给你一个 \(n\) 的排列 \(\{p_n\}\)，以及排列中第 \(i\) 个数的颜色 \(c_i\)。

令两个排列 \(A\) 和 \(B\) 的乘积 \(C=A\times B\) 满足 \(C_i=A_{B_i}\)。

对于排列 \(p\)， \(p^k=\underbrace{p \times p \times \cdots \times p}_{k\ p}\)。

求最小的 \(k\)，使 \(P=p^k\) 中存在 \(i\) 满足 \(c_i=c_{P_i}=c_{P_{P_i}}=\cdots\)。

数据范围：\(1\le T\le 10^4\)，\(1\le n,\sum n\le 2\times 10^5\)。

---

可以把每个 \(p_i\) 看做一条 \(i\to p_i\) 的边。

因为 \(p\) 是个排列，所以会形成多个环，每个点每条边都在一个环上。

所以可以单独考虑每个环的最小 \(k\)，然后答案取其最小值。

设当前环大小为 \(sz\)：

\(k\) 每 \(+1\) 就使原来的边 \(i\to p^k_{i}\) 变成了 \(i\to p^{k+1}_{i}\)。

设 \(g=\gcd(k,sz)\)，很明显 \(p^k\) 的图中每个环元素和 \(p^g\) 中的一样。

所以只需考虑 \(k\) 是 \(sz\) 的因数的情况：

每一整个大环会被分成 \(\frac{sz}{k}\) 个环，环上相邻元素在原环上距离为 \(k\)。

然后对 \(\frac{sz}{k}\) 个环判断是否颜色相等，如果有颜色相等的环，就说明对于该环该 \(k\) 是合法的。

然后枚举 \(k\)，找到最小合法 \(k\) 即可。

时间复杂度 \(\Theta(n\sigma(n))\)（\(\sigma(n)\) 表示 \(n\) 的约数个数）。

---

蒟蒻讲不清楚，放个只有一个环情况的例图：

---

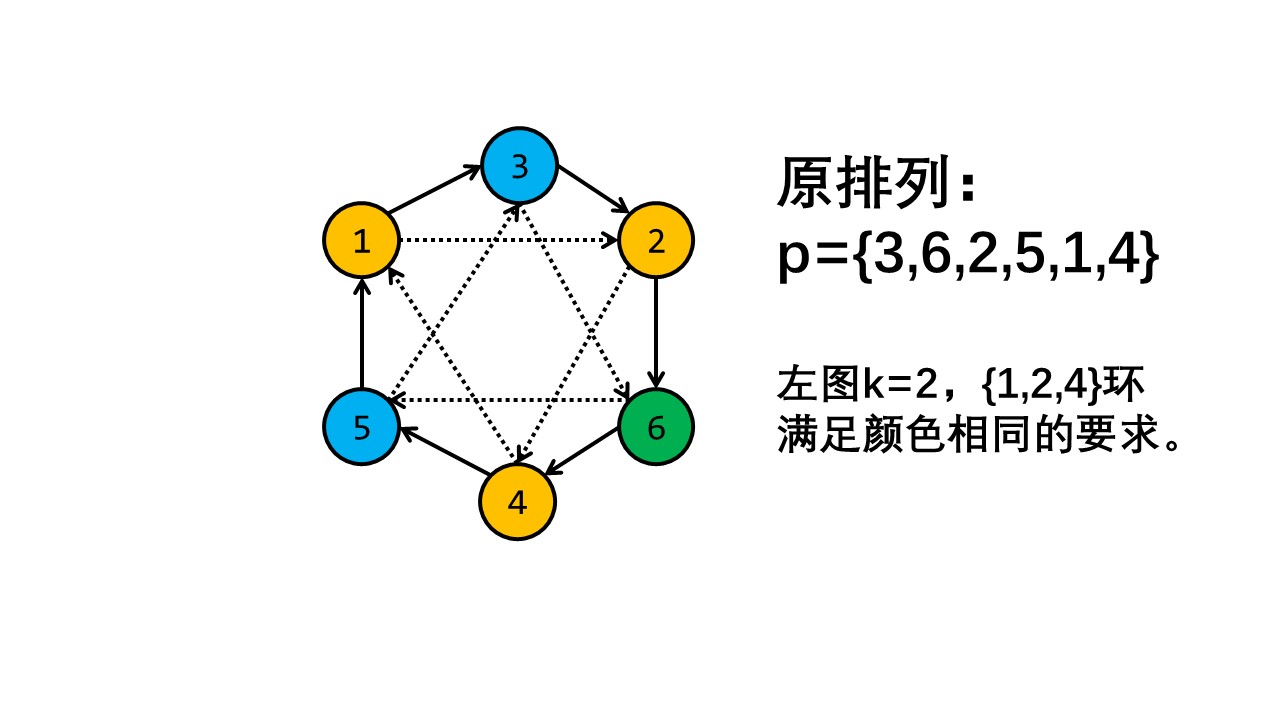
\(\texttt{vector}\) 代码实现：

#include <bits/stdc++.h>
using namespace std;

//&Start
#define re register
#define il inline
#define inf 0x3f3f3f3f
typedef long long lng;

//&Data
#define N 200000
bitset<N+5> vis;

//&Main
int main(){
	re int t,n,ans;
	scanf("%d",&t); //多组测试数据！
	for(re int ti=1;ti<=t;ti++){
		scanf("%d",&n);
		vector<int> p(n+1),c(n+1);
		for(re int i=1;i<=n;i++) scanf("%d",&p[i]);
		for(re int i=1;i<=n;i++) scanf("%d",&c[i]);
		vis.reset(),ans=inf;
		for(re int i=1;i<=n;i++)if(!vis[i]){ //如果该点未出现于之前的环
			vector<int> C,d; //C:该环上的点的颜色，d:sz的因素
			for(re int j=i,f=1;f||j!=i;f=0,j=p[j]) C.push_back(c[j]),vis[j]=1;
			re int sz=C.size(),K;
			for(re int j=1;j<=sz;j++)if(sz%j==0) d.push_back(j);
			for(re int k:d){
				re int ok=0;
				for(re int s=0;s<k;s++){
					re int samc=1;
					for(re int j=s;j<sz;j+=k)if(C[j]!=C[s]){samc=0;break;} //判断环上点颜色相等
					if(samc){ok=1;break;}
				}
				if(ok){K=k;break;}
			}
			ans=min(ans,K); //取k最小值
		}
		printf("%d\n",ans);
	}
	return 0;
}

---

祝大家学习愉快！