学习笔记：Splay

代码适中、非常灵活的平衡树。

需要前置：二叉搜索树。

一些基础的函数：

int idx, ch[N][2], cnt[N], sz[N], fa[N];
/*
idx 是节点计数, ch[i][0 / 1] 是 i 节点的左右子树节点
cnt[i] 是 i 节点的数量
sz[i] 是 i 节点子树的大小
fa[i] 是 i 的父亲
*/

// pushup
void inline pushup(int p) {
	sz[p] = sz[ch[p][0]] + cnt[p] + sz[ch[p][1]];
}

// 判断 p 是 fa[p] 左儿子还是右儿子 (0 / 1)
bool inline get(int p) {
	return p == ch[fa[p]][1];
}

// 清空一个节点
void inline clear(int p) {
	ch[p][0] = ch[p][1] = val[p] = cnt[p] = sz[p] = fa[p] = 0;
}

\(\text{Pushup}\) 要放在旋转的最后。

\(\text{Pushdown}\) 只要递归就推下去。

旋转的意义：保持中序遍历不变，调整树高。

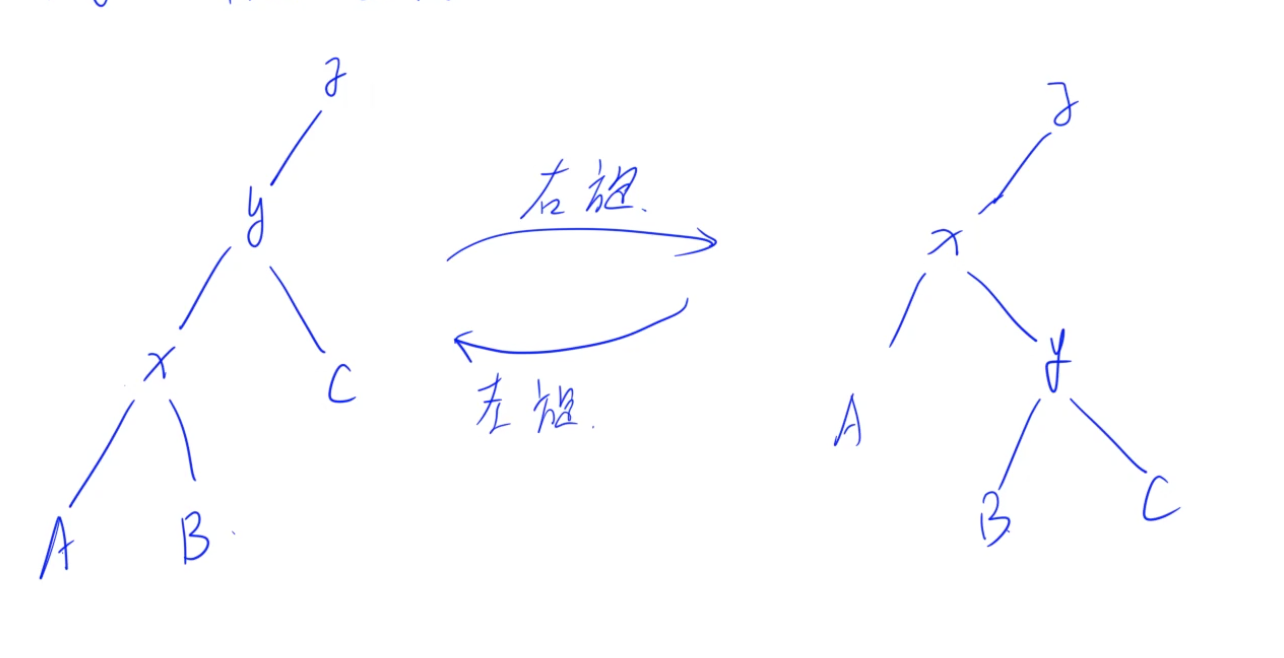
这样旋转后，在改变树形结构的基础上发现中序遍历保持不变。

void inline rotate(int x) {
	int y = fa[x], z = fa[y], k = get(x);
	ch[y][k] = ch[x][!k], fa[ch[x][!k]] = y;
	ch[x][!k] = y, fa[y] = x;
	fa[x] = z;
	if (z) ch[z][y == ch[z][1]] = x;
	pushup(y); pushup(x);
}

以下所有介绍的操作都是 Splay 的独特的操作，剩下的二叉搜索树就有了。

复杂度的保持 & 核心思想：

每次操作完的点，均将这个点旋转（Splay）到树根。

感性理解的好处：每一次用到，后面还有可能再用到。

有严谨的证明，结论是若操作 \(m\) 次，总复杂度是 \(O(m \log n)\)，平均意义每次操作都是 \(O(\log)\) 的。

Splay 翻转

定义函数 \(splay(x, k)\) 表示将点 \(x\) 旋转至 \(k\) 下面。

\(y = fa_x, z = fa_y\)。

迭代：

• 如果 \(z\) 不存在，转一次 \(x\) 即可。
• 若 \(z, y, x\) 是直线，那么先把 \(y\) 转上去，然后转 \(x\)
• 否则是折线，就转两次 \(x\)

只有这么转复杂度才是对的，不能随便转，要背一下）

void inline splay(int p) {
	for (int f = fa[p]; f = fa[p]; rotate(p))
		if (fa[f]) rotate(get(p) == get(f) ? f : p);
	rt = p;
}

以下标为键：将一段序列插入到 y 的后面

• 找到 \(y\) 的后继 \(z\)
• 将 \(y\) 旋转到根 \(splay(y, 0)\)
• 将 \(z\) 转到 \(y\) 的下面 \(splay(z, y)\)

这样 \(z\) 一定没有左子树，直接把一段序列构造好的树节点赋值成 \(z\) 的左子树就行了。

以下标为键：操作一段

删除序列的 \([l, r]\)

\(splay(kth(l - 1), 0), splay(kth(r+1), l - 1)\)，这样 \([l, r]\) 之间所有的点组成了以 \(r + 1\) 的左子树，这样直接就可以在 \(kth(r + 1)\) 的左儿子这个节点打 \(tag\) 就行了。

板子

P3369 【模板】普通平衡树

#include <cstdio>
#include <iostream>

using namespace std;

const int N = 100005;

int n, m, rt;
int idx, ch[N][2], val[N], cnt[N], sz[N], fa[N];

void inline update(int p) {
	sz[p] = sz[ch[p][0]] + cnt[p] + sz[ch[p][1]];
}

bool inline get(int p) {
	return p == ch[fa[p]][1];
}

void inline clear(int p) {
	ch[p][0] = ch[p][1] = val[p] = cnt[p] = sz[p] = fa[p] = 0;
}

void inline rotate(int x) {
	int y = fa[x], z = fa[y], k = get(x);
	ch[y][k] = ch[x][!k], fa[ch[x][!k]] = y;
	ch[x][!k] = y, fa[y] = x;
	fa[x] = z;
	if (z) ch[z][y == ch[z][1]] = x;
	update(y); update(x);
}

void inline splay(int p) {
	for (int f = fa[p]; f = fa[p]; rotate(p))
		if (fa[f]) rotate(get(p) == get(f) ? f : p);
	rt = p;
}

void insert(int &p, int x, int f) {
	if (!p) {
		p = ++idx, sz[p] = cnt[p] = 1, fa[p] = f, val[p] = x;
		if (f) ch[f][x > val[f]] = p, update(f), splay(p);
	} else if (val[p] == x) cnt[p]++, sz[p]++, update(f), splay(p);
	else insert(ch[p][x > val[p]], x, p);
}

int kth(int p, int k) {
	if (k <= sz[ch[p][0]]) return kth(ch[p][0], k);
	else if (k <= sz[ch[p][0]] + cnt[p]) { splay(p); return val[p]; }
	else return kth(ch[p][1], k - sz[ch[p][0]] - cnt[p]);
}

int getRank(int p, int k) {
	int res = 0;
	if (k < val[p]) return getRank(ch[p][0], k);
	else if (k == val[p]) { res = sz[ch[p][0]] + 1; splay(p); return res; }
	else { res += sz[ch[p][0]] + cnt[p]; return res + getRank(ch[p][1], k); }
}

int inline pre() {
	int p = ch[rt][0];
	while (ch[p][1]) p = ch[p][1];
	splay(p);
	return p;
}

int inline nxt() {
	int p = ch[rt][1];
	while (ch[p][0]) p = ch[p][0];
	splay(p);
	return p;
}

void inline del(int k) {
	getRank(rt, k);
	if (cnt[rt] > 1) cnt[rt]--, sz[rt]--;
	else if (!ch[rt][0] && !ch[rt][1]) {
		clear(rt), rt = 0;
	} else if (!ch[rt][0]) fa[rt = ch[rt][1]] = 0;
	else if (!ch[rt][1]) fa[rt = ch[rt][0]] = 0;
	else {
		int p = rt, x = pre();
		splay(x); ch[x][1] = ch[p][1], fa[ch[x][1]] = x;
		clear(p); update(rt);
	}
}

int main() {
	scanf("%d", &m);
	while (m--) {
		int opt, x; scanf("%d%d", &opt, &x);
		if (opt == 1) {
			insert(rt, x, 0);
		} else if (opt == 2) {
 			del(x);
		} else if (opt == 3) {
			insert(rt, x, 0);
			printf("%d\n", getRank(rt, x));
			del(x);
		} else if (opt == 4) {
			printf("%d\n", kth(rt, x));
		} else if (opt == 5) {
			insert(rt, x, 0);
			printf("%d\n", val[pre()]);
			del(x);
		} else if (opt == 6) {
			insert(rt, x, 0);
			printf("%d\n", val[nxt()]);
			del(x);
		}
	}
}

P3391 【模板】文艺平衡树

#include <iostream>
#include <cstdio>
#define ls ch[p][0]
#define rs ch[p][1]
#define get(x) x == ch[fa[x]][1]
using namespace std;

const int N = 100005;

int n, m, val[N], ch[N][2], sz[N], fa[N], rev[N], rt, idx;

void inline pushup(int p) {
    sz[p] = sz[ls] + sz[rs] + 1;
}

void inline reverse(int p) {
    swap(ls, rs), rev[p] ^= 1;
}

void inline pushdown(int p) {
    if (rev[p]) {
        if (ls) reverse(ls);
        if (rs) reverse(rs);
        rev[p] = 0;
    }
}

void inline rotate(int x) {
    int y = fa[x], z = fa[y], k = get(x);
    ch[y][k] = ch[x][!k], fa[ch[x][!k]] = y;
    ch[x][!k] = y, fa[y] = x;
    fa[x] = z;
    if (z) ch[z][y == ch[z][1]] = x;
    pushup(y), pushup(x);
}

void inline splay(int x, int k) {
    for (int f = fa[x]; (f = fa[x]) != k; rotate(x)) {
        if (fa[f]) rotate(get(x) == get(f) ? f : x);
    }
    if (!k) rt = x;
}

void build(int &p, int l, int r, int f) {
    if (l > r) return;
    p = ++idx;
    int mid = (l + r) >> 1; val[p] = mid, fa[p] = f;
    if (l < r) {
        build(ch[p][0], l, mid - 1, p);
        build(ch[p][1], mid + 1, r, p);
    }
    pushup(p);
}

void print(int p) {
    if (!p) return;
    pushdown(p);
    print(ch[p][0]);
    if (val[p] && val[p] <= n) printf("%d ", val[p]);
    print(ch[p][1]);
}

int inline kth(int p, int k) {
    pushdown(p);
    if (k <= sz[ch[p][0]]) return kth(ch[p][0], k);
    else if (k == sz[ch[p][0]] + 1) {
        splay(p, 0);
        return p;
    } else return kth(ch[p][1], k - sz[ch[p][0]] - 1);
}

int main() {
    scanf("%d%d", &n, &m);
    build(rt, 0, n + 1, 0);
    while (m--) {
        int l, r; scanf("%d%d", &l, &r);
        int x = kth(rt, l), y = kth(rt, r + 2);
        splay(x, 0); splay(y, x);
        reverse(ch[y][0]);
    }
    print(rt);
    return 0;
}