编程与算法（一）、C语言实现二分法（方程近似解）

一、二分法

假设有这样一个函数f(x)

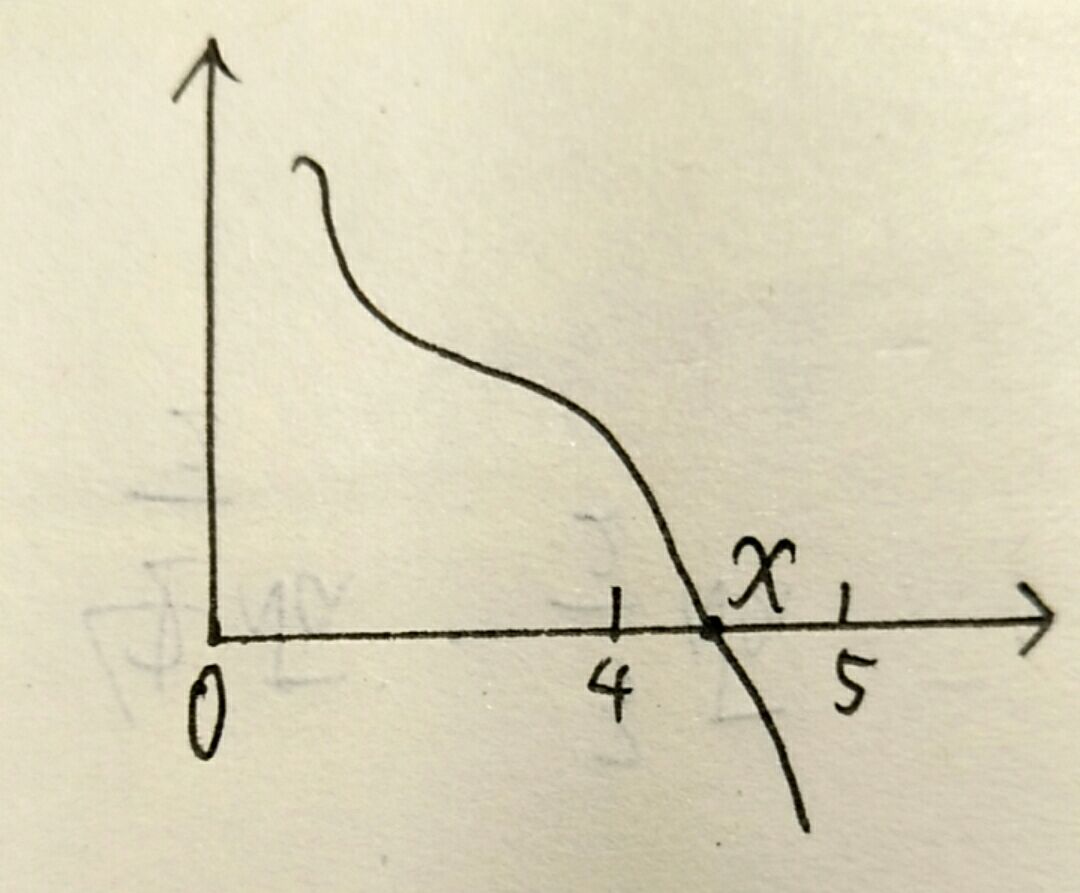
函数与x轴有一个交点（也就是f(a)*f(b)<0，a<b），现在我们要求这个点的x值，也就是方程f(x)=0的一个实根

直接解显然不合适，那么接下来就轮到二分法出场了。

从图中可以看出4<x<5，我们把[4,5]称为这个根的一个隔离区间（记作[a,b]），你可以把它想象成一个夹板，把我们要求的数（记作ξ）夹在中间，

那么我们只需要不断缩小夹板间的距离就能求出较为精确的ξ值了。

首先，我们取隔离区间的中点(a+b)/2，

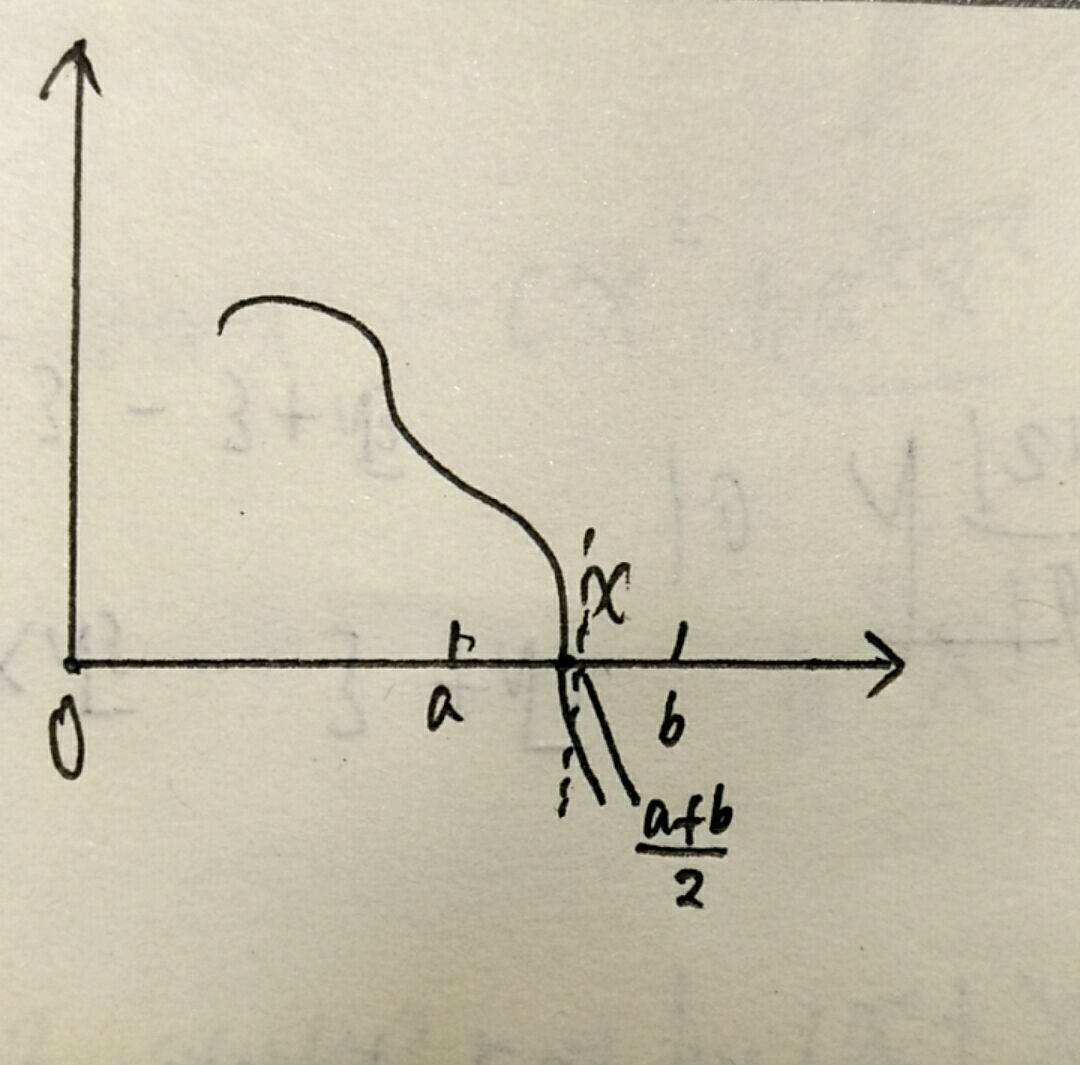
如图，令e=(a+b)/2，如果f(e)=0，那么e就是我们要找的ξ值，如果f(e)和f(a)同号，那么说明这两点都在ξ的同一边，用e替换掉a，

同理，如果f(e)和f(b)同号，用e替换掉b，这样就实现了对ξ的不断逼近，循环n次后误差小于(1/(2^n))*(b-a)。

二、代码实现

废话不多说，直接上代码

 double dichotomy(int n, double a, double b, double (*f)(double))
 {
     double f_a = (*f)(a);
     double f_b = (*f)(b);
     int i = ;
     double e;
     while ()
     {
         e = (a + b) / 2.0;
         if (i != n)
         {
             double f_e = (*f)(e);
             if (f_e == )
             {
                 return e;
             }
             else
             {
                 if (f_a * f_e > )
                 {
                     a = e;
                 }
                 else
                 {
                     b = e;
                 }

             }
             ++i;
         }
         else
         {
             return e;
         }

     }
 }

二分法的一个例子就是计算根号二（1.4142135623730951），也就是解x^2 - 2 = 0这个方程，代码如下

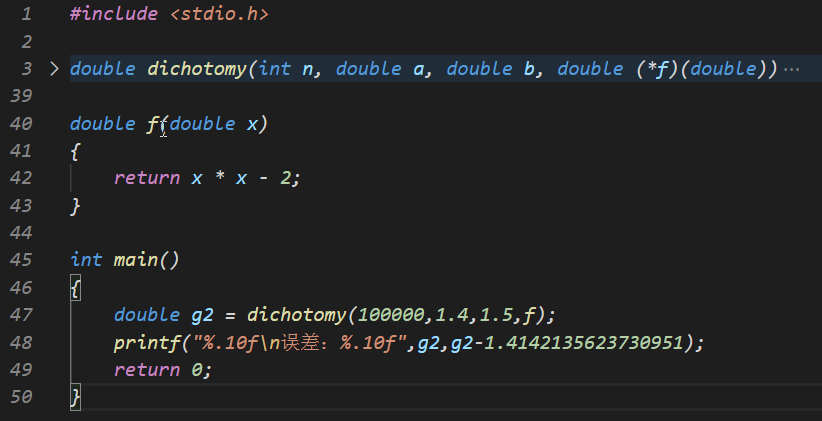
运行效果：

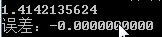
当然，你可以把dichotomy的int n换成long long int n，然后输入一个超大的数，就可以获得更加精确的根号二。