Manacher (马拉车) 算法：解决最长回文子串的利器

最长回文子串

回文串就是原串和反转字符串相同的字符串。比如 aba，acca。前一个是奇数长度的回文串，后一个是偶数长度的回文串。

最长回文子串就是一个字符串的所有子串中，是回文串且长度最长的子串。

Brute Force 做法

枚举所有子串，判断是否是回文串，然后寻找最大长度。寻找所有子串要两重循环，判断是否是回文要一重循环，总体时间复杂度 \(O(n^3)\)。

稍微优化一下，可以枚举对称中心，然后向两边扩展，直到遇到两个不同的字符，枚举下一个对称中心，寻找其中的最大长度，时间复杂度 \(O(n^2)\)。

还可以使用 DP 解决，求原串与反转字符串的最长公共子序列 (LCS)，时间复杂度 \(O(n^2)\)。

Manacher 算法

接下来就是重点了，Manacher 算法，在1975年由一个叫 Manacher 的人发明的。能够在 O(n) 的时间求得最长回文子串。

前面提到，回文串有奇数长度的和偶数长度的，分类讨论有些复杂，可以参考这里。为了避免分类讨论，可以使用一个技巧：在字符串首尾以及每两个字符之间插入一个 '#'。比如 abaacca，转换后就是 #a#b#a#a#c#c#a#。那么不管是奇回文 aba 还是偶回文 acca，转换后都是奇回文 (#a#b#a# 和 #a#c#c#a#)。

string init(string s) {
    string res;
    res += '@';  // 在开头加入哨兵防止越界
    for(int i = 0; i < s.size(); ++i) {
        res += '#';
        res += s[i];
    }
    res += '#';
    res += '$';  // 结尾同样加入哨兵防止越界
    return res;
}

\(Manacher\) 算法的思想来自于上述枚举对称中心的思想。该算法需要维护一个 \(len\) 数组，\(len[i]\) 代表 \(i\) 为中心的最长回文子串的长度。

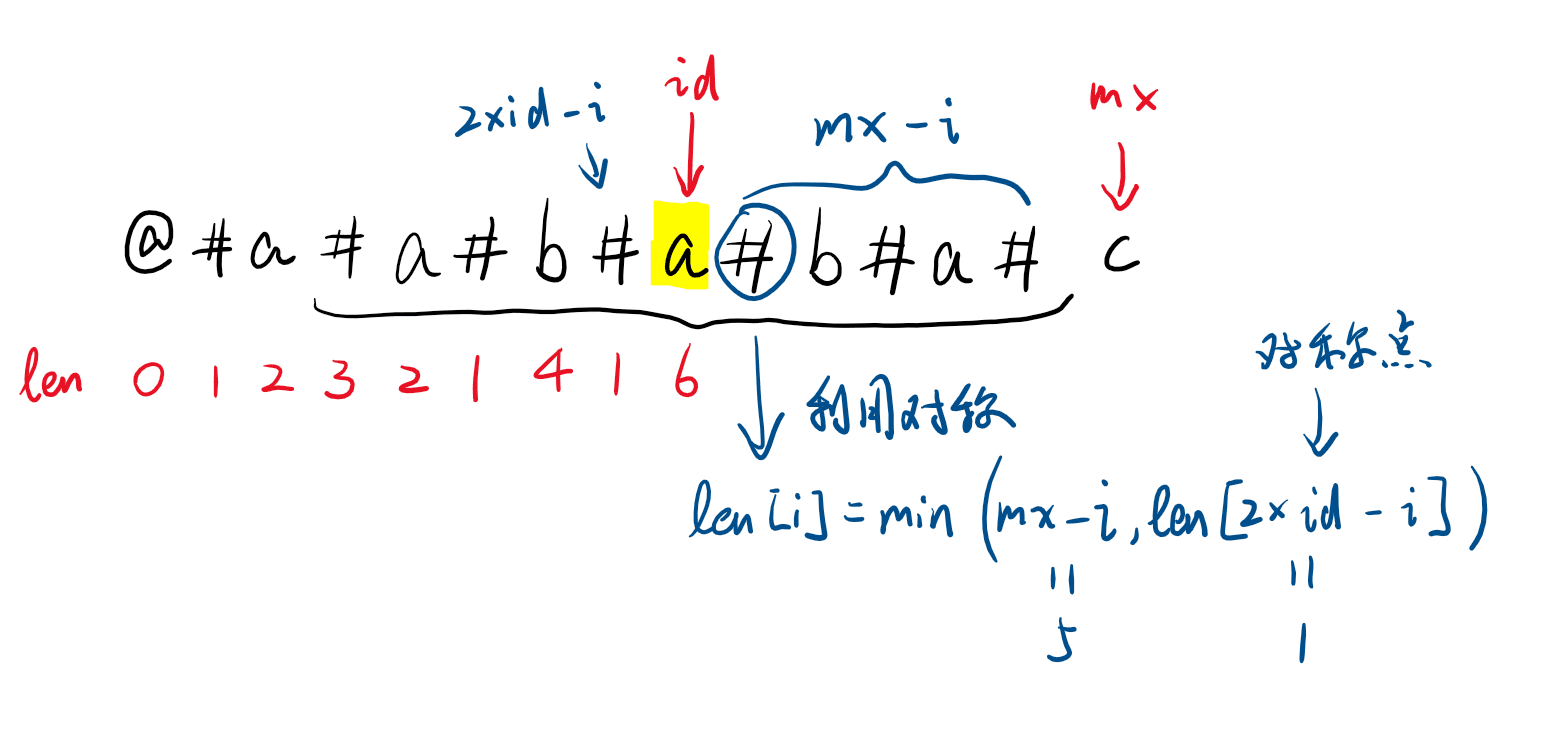
设 \(s\) 为原字符串，\(mx\) 为之前计算的回文串中右端点的最大值，这个回文串的中心位置为 \(id\)，也就是 \(mx=id+len[id]\)。

每次计算的时候，id 的右边和左边是对称的，因此计算右边的时候不需要用从对称中心向两边扩展的思想，而是只用一行代码解决：len[i] = min(mx - i, len[2 * id - i]);，这也是 Manacher 中最关键的一行代码。

如下图所示，\(id\) 右边到 \(mx\) 之间的子串与 \(id\) 左边是对称的，所以右边的 \(len[i]\) 最大长度为左边与之对称的 \(len[2×id−i]\)，由于右边的回文串不能超过 \(mx\) (原因见第 2 张图)，所以 len[i] = min(mx - i, len[2 * id - i]);。

\(id\) 右边的回文串长度不能超过 \(mx−i\) 的原因是，如果 \(len[2∗id−i]\) 更长，如下图的黄色部分，那么右边的黄色部分与左边的黄色部分相同，那么黑色部分应该可以更长，产生矛盾。

理解了上面的内容基本上就理解了 \(Manacher\) 算法了。

代码实现如下：

如果觉得这个代码解释的不太清楚的话可以直接看下面的模板题或者看下刘毅学长的代码

int Manacher(string s) {
    memset(len, 0, sizeof(len));
    int mx = 0, id = 0;
    int ans = 0;
    for(int i = 1; i < s.size() - 1; ++i) {
        if(mx > i) {
            len[i] = min(mx - i, len[2 * id - i]);  // 上面提到的最关键的一行代码
        } else {
            len[i] = 1;  // 如果 i 超过右边界要从头计算
        }
        while(s[i - len[i]] == s[i + len[i]]) {  // 从头计算的方法，就是上面提到的从中心向两边扩展
            ++len[i];
        }
        // 更新 mx 和 id
        if(i + len[i] > mx) {
            mx = i + len[i];
            id = i;
        }
        ans = max(ans, len[i]);
    }
    return ans - 1; // len[i] 中的最大值-1 即为原串的最长回文子串长度
}

模板题：HDU 3068 最长回文

题目链接：HDU 3068 最长回文

// Author : RioTian
// Time : 20/11/11
#include <bits/stdc++.h>
#define ms(a, b) memset(a, b, sizeof(a))
using namespace std;
const int maxn = 220000;
int len[maxn];
string init(string s) {
    string res;
    res += '@';
    for (int i = 0; i < s.size(); ++i) {
        res += '#';
        res += s[i];
    }
    res += '#';
    res += '$';
    return res;
}
int Manacher(string s) {
    ms(len, 0);
    int mx = 0, id = 0;
    int ans = 0;
    for (int i = 1; i < s.size() - 1; ++i) {
        if (mx > i)
            len[i] = min(mx - i, len[2 * id - i]);
        else
            len[i] = 1;

        while (s[i - len[i]] == s[i + len[i]]) ++len[i];

        if (i + len[i] > mx) {
            mx = i + len[i];
            id = i;
        }
        ans = max(ans, len[i]);
    }
    return ans - 1;
}

int main() {
    // freopen("in.txt", "r", stdin);
    ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
    string s;
    while (cin >> s) {
        string tmp = init(s);
        cout << Manacher(tmp) << endl;
    }
}

参考

OI wiki

刘毅学长关于马拉车算法的讲解