清北澡堂 Day2 下午 一些比较重要的数论知识整理
1.欧拉定理
设x1,x2,.....,xk,k=φ(n)为1~n中k个与n互质的数
结论一:axi与axj不同余
结论二:gcd(axi,n)=1
结论三:x1,x2,...,xk和ax1,ax2,...,axk一一对应
结论四:aφ(n)≡1(mod n)
计算:φ(m)=m*(1-1/p1)*......*(1-1/pi)
Back to here
请证明:如果n为素数,取a<n,设n-1=d*2r,则要么ad≡1(mod n)要么存在0<=i<r,使得ad*2^t≡-1(mod n),要么存在0<=i<r,使得ad*2^t≡-1(mod n)
证:由费马小定理得an-1≡1(mod n),已知n-1=d*2r
∴ad*2^r≡1(mod n)
∴ad*2^r-1≡0(mod n)
由平方差公式知:(ad*2^(r-1))(ad*2^(r-1))≡0(mod n)
∴原式=(ad-1)(ad+1)(ad*2+1)(ad*2^2).......(ad*2^(r-1)+1≡0(mod n)
2.线性求逆元
求1~n所有数 对p的逆元(p为质数)
为了减少时间,我们要尽量利用已经求出来的逆元进行计算,也就是说,当求i的逆元时,1~i-1的逆元已经求完了
设1<=i<=n
∵p/i=k......r
∴p=ik+r
ik+r≡0 (mod p)
kr-1+i-1≡0 (mod p)
i-1≡-kr-1 (mod p)

最后一步把k和r带进去就可以得到
卡n log n的复杂度用到
3.BSGS算法(baby-step gaint-step)
问题:求ax≡b (mod m)的最小正整数解(m为质数)
如果枚举:复杂度为O(m)
考虑分块

能否从其中某一行找到答案
从第二行找答案等价于第一行里面是否存在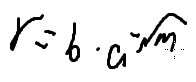
从第三行找答案等价于第二行里面是否存在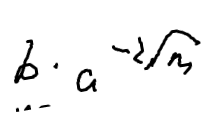
先暴力出第一行,再排序二分,这样求每一行都可以化成第一行
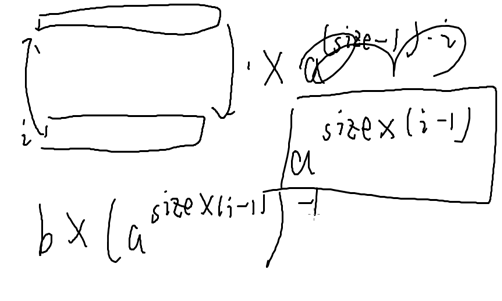
代码如下:
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<cstdlib>
using namespace std;
int size,a,b,p,z[];
bool erfen(int x)//二分查找答案
{
int l=,r=size;
while (l+!=r)
{
int m=(l+r)>>;
if (z[m]>=x) r=m;
else l=m;
}
return z[r]==x;
} int powmod(int x,int y,int z)
{
int i=x;
int s=;
while(y)
{
if(y&)
{
s=(s*i)%z;
}
i=(i*i)%z;
y>>=;
}
return s%z;
} int bsgs(int a,int b,int p)//bsgs算法
{
size=sqrt(p);//分块 int nowv=;
for(int i=;i<=size;i++)
{
nowv = (long long) nowv*a%p;//枚举
z[i] = nowv;
if(z[i]==b) return ;
}
sort(z+,z+size+);
for(int i=;(i-)*size+<=p;i++)
{
int y=(long long)b*powmod(powmod(a,size*(i-),p),p-,p);
if(erfen(y))
{
for(int j=(i-)*size+;j<=i*size;j++)
if(powmod(a,j,p)==b) return j;
}
}
return -;
} int main()
{
cin>>a>>b>>p;
cout<<bsgs(a,b,p);
return ;
}
i-1行*size个数+1
4.数论函数
喂正整数吐整数
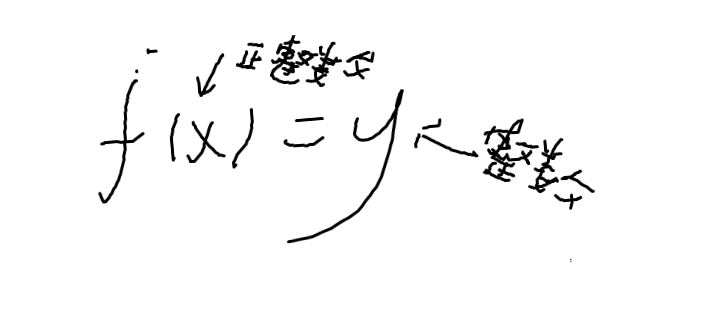
积性函数
积性函数:当gcd(a,b)=1时,ƒ(ab)=ƒ(a)ƒ(b)
完全积性函数:ƒ(ab)=f(a)f(b)
积性函数包括:
不变函数:ƒ(n)=n
欧拉函数:ƒ(n)=φ(n)
莫比乌斯函数:ƒ(n)=μ(n)
因子数目总数:ƒ(n)=d(n)
因子之和函数:ƒ(n)=σ(n)


如μ(4)=0
μ(15)=1
μ(1001)=-1
φ和μ的实现:考虑线性筛,降低复杂度
代码如下:
memset(not_prime,,sizeof(not_prime)); for (int i=;i<=n;i++)
{
if (!not_prime[i])
{
prime[++ prime_cnt] = i;
phi[i] = i-;
mu[i] = -;
}
for (int j=;j<=prime_cnt;j++)
{
int x = i * prime[j];
if (x>n) break; not_prime[x] = true;
phi[x] = phi[i] * phi[prime[j]];
mu[x] = mu[i] * mu[prime[j]]; if (i % prime[j] == )
{
phi[x] = phi[i] * prime[j];
mu[x] = ;
break;
}
}
}

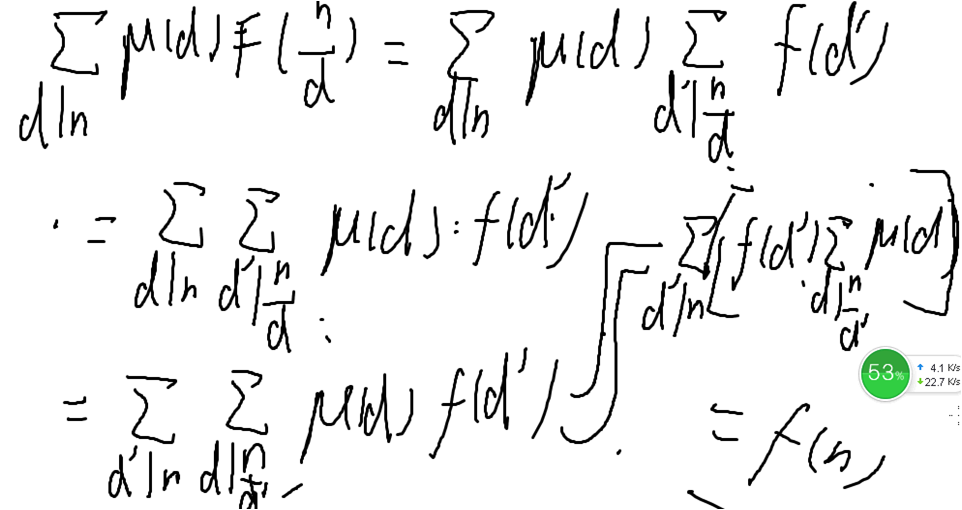
清北澡堂 Day2 下午 一些比较重要的数论知识整理的更多相关文章
- 清北澡堂 Day2 上午 一些比较重要的关于数论的知识整理
1.算数基本定理: 对于任意的大于1的正整数N,N一定能够分解成有限个质数的乘积,即 其中P1<P2<...<Pk,a1,a2,...,ak>=1; 证: 存在性: 若存在最小 ...
- 清北澡堂 Day 3 上午
1.数论函数的卷积公式 (ƒ*g)(n)=Σd|nƒ(d)×g(n/d) 已知f*[1~n],g[1~n] 怎么求(f*g)[1~n]? 一个个求复杂度O(n根号n) 如何加速? 考虑更换枚举顺序(这 ...
- 清明培训 清北学堂 DAY2
今天是钟皓曦老师的讲授~~ 总结了一下今天的内容: 数论!!! 1.整除性 2.质数 定义: 性质: 3.整数分解定理——算数基本定理 证明: 存在性: 设N是最小不满足唯一分解定理的整数 (1) ...
- 清北学堂Day2
算数基本定理: 1.整数及其相关 2.唯一分解定理 对于任意的大于1的正整数N,N一定能够分解成有限个质数的乘积,即 其中P1<P2<...<Pk,a1,a2,...,ak>= ...
- 五一培训 清北学堂 DAY2
今天还是冯哲老师的讲授~~ 今日内容:简单数据结构(没看出来简单qaq) 1.搜索二叉树 前置技能 一道入门题在初学OI的时候,总会遇到这么一道题.给出N次操作,每次加入一个数,或者询问当前所有数的最 ...
- 清北Day4
版权声明:如需转载请标明出处,未得到本人许可请勿转载. 今天就可以看到传说中的 数据结构 嘿嘿嘿嘿 都有什么呢 链表 队列 栈 st表 hash 线段树 树链剖分 一.栈: 放出来这个看烂了的图 值得 ...
- 济南清北学堂游记 Day 1.
快住手!这根本不是暴力! 刷了一整天的题就是了..上午三道题的画风还算挺正常,估计是第一天,给点水题做做算了.. rqy大佬AK了上午的比赛! 当时我t2暴力写挂,还以为需要用啥奇怪的算法,后来发现, ...
- 清北学堂2017NOIP冬令营入学测试P4745 B’s problem(b)
清北学堂2017NOIP冬令营入学测试 P4745 B's problem(b) 时间: 1000ms / 空间: 655360KiB / Java类名: Main 背景 冬令营入学测试 描述 题目描 ...
- 清北学堂2017NOIP冬令营入学测试 P4744 A’s problem(a)
清北学堂2017NOIP冬令营入学测试 P4744 A's problem(a) 时间: 1000ms / 空间: 655360KiB / Java类名: Main 背景 冬令营入学测试题,每三天结算 ...
随机推荐
- jquery中点击切换的实现
项目中经常会遇到一种情况,就是点击切换,比如点击按钮,div样式为1,再点击一下按钮,div样式为2,再点击一下按钮,div样式为1.需要自定义jQuery方法toggle. // toggle方法 ...
- 【代码笔记】Web-CSS-CSS Fonts(字体)
一,效果图. 二,代码. <!DOCTYPE html> <html> <head> <meta charset="utf-8"> ...
- 在 Apex 中得到 sObject 的信息
Salesforce 的数据模型是基于 sObject 的.在 Apex 中,所有的标准对象.自定义对象都是继承自 sObject 的. 关于在 Apex 中得到 sObject 的信息,我们要基于两 ...
- Android ScrollView和ListView滑动冲突解决记录
private int mLastX; private int mLastY; public View.OnTouchListener onTouchListener = new View.OnTou ...
- JHipster技术栈定制 - 基于UAA的微服务之间安全调用
本文通过代码实例演示如何通过UAA实现微服务之间的安全调用. uaa: 身份认证服务,同时也作为被调用的资源服务.服务端口9999. microservice1: 调用uaa的消费者服务,服务端口80 ...
- java中split特殊符号
关于点的问题是用string.split("[.]") 解决. 关于竖线的问题用 string.split("\\|")解决. 关于星号的问题用 string. ...
- VS2017在线安装包下载
VS2017个人免费版即社区官方下载地址为:https://download.microsoft.com/download/D/1/4/D142F7E7-4D7E-4F3B-A399-5BACA91E ...
- Bootstrap -- 导航栏样式、分页样式、标签样式、徽章样式
Bootstrap -- 导航栏样式.分页样式.标签样式.徽章样式 1. 使用图标的导航栏 使用导航栏样式: <!DOCTYPE html> <html> <head&g ...
- MongoDB的常用命令和增查改删
数据库操作 Mongodb MySQL 查询库 show databases | show dbs show databases 选中库 use databaseName use databaseNa ...
- django自定义分页器
一 django 的分页器 1 批量创建数据 批量导入数据: Booklist=[] for i in range(100): Booklist.append(Book(title="boo ...
