2017-9-24模拟赛T1 个人卫生综合征(school.*)

题目

---

每天 BBS 都要从家里经过城市中的一段路到学校刷五三。城市中一共有 n 个路口
和 m 条双向道路，每条双向道路都连接着两个路口 a i 、b i 且有一定的时间花费 v i 。BBS
家编号为 1，学校编号为 n。今天，BBS 由于个人卫生综合征导致他很迟才离开家，他
想用膜法改变 k 条道路的长度使通过其的时间花费 v i 变为 0。现在他问你改变道路长度
之后他到学校的最小时间花费是多少？
输入格式：
第一行为三个整数 n、m、k，接下来的 m 行每行三个整数 a i ,b i ,v i ，分别表示这条路连
着的两个路口和通过其所用的时间。
输出格式：
一个整数，表示 BBS 到学校的最小时间花费。

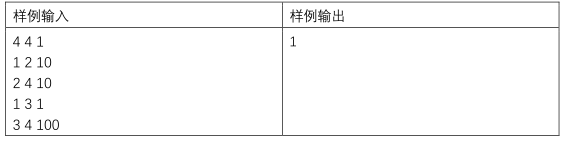
样例解释：
更新 3->4 的道路，最短路线为 1->3->4，用时为 1+0=1。
数据范围：
对于 100%的数据：1<=n<=10000，1<=m<=50000，1<=k<=20，1<=v i <=1000000。

题解

---

题意还是比较易懂的。给定一个无向图，可以把k条路的长度变为0，求1到n的最短路。

这题似乎没有部分分……那就讲正解吧。

插播：话说这题是有原题的：(BZOJ2763)[JLOI2011]飞行路线。

这题的正解是分层图最短路。

建立一个有k+1个层的图，每次将花费变为0，层数+1，初始0层，最多k层，所以最多减少k条路。（当然，一条路减少多次是没有意义的）

在实际应用时，由于图是一样的，只需要分别记录这k层中每层n个点到1号点的最短路(代码中的d数组)和访问情况(代码中的vis数组)即可。

还有，一定要用dijkstra！一定要用dijkstra！一定要用dijkstra！用spfa会T！(某巨神就中招了……)

代码

---

 #include <stdio.h>
 #include <string.h>
 #include <queue>
 #define N 10005
 #define K 22
 using namespace std;
 int n,m,k,d[N][K];char vis[N][K];
 int ne=,h[N];struct edge{int to,w,x;}e[];
 inline void ins(int s,int t,int w) {
     e[++ne].to=t;e[ne].w=w;e[ne].x=h[s];h[s]=ne;
 }
 struct node {
     int a,l,dis;
     bool operator<(const node &b)const {
         return dis>b.dis;
     }
 };
 priority_queue<node> q;
 inline void tt(int a,int l,int p) {
     if(!vis[a][l]&&d[a][l]>p) {
         d[a][l]=p;
         q.push({a,l,p});
     }
 }
 void dijkstra() {
     node u;edge v;
     memset(d,,sizeof(d));
     d[][]=;
     q.push({,,});
     while(!q.empty()) {
         u=q.top();q.pop();
         vis[u.a][u.l]=;
         for(int i=h[u.a];i;i=v.x) {
             v=e[i];
             tt(v.to,u.l,u.dis+v.w);
             if(u.l<k) tt(v.to,u.l+,u.dis);
         }
     }
 }
 int main() {
     int a,b,c;
     scanf("%d%d%d",&n,&m,&k);
     for(int i=;i<m;++i) {
         scanf("%d%d%d",&a,&b,&c);
         ins(a,b,c);ins(b,a,c);
     }
     dijkstra();
     a=d[n][];
     for(int i=;i<=k;++i) if(d[n][i]<a) a=d[n][i];
     printf("%d",a);
     return ;
 }