清北学堂学习总结day1

上午篇

一、高精度计算；

【以下内容先只考虑非负数情况】

•高精度加法：

思路：【模拟竖式运算】

注意：【进位】

•高精度减法：

思路：【同加法类似，模拟竖式运算，进位变退位】

注意: 【结果为负数的情况（一会儿讲到）】

•高精度乘法：

思路：【类似，模拟竖式运算，考虑进位】

注意：【结果为0的情况】

附总代码：

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<cstdlib>
using namespace std;
char str[];
int a[],b[],c[];
int main(){
    scanf("%s", str);
    int len=strlen(str);
    //  '36'
    for(int i=len-;i>=;i--)a[len-i]=str[i]-'';
//    scanf("%s", str);
    int n=len;
    /*len=strlen(str);
    //  '36'
    for(int i=len-1;i>=0;i--)b[len-i]=str[i]-'0';
    int m=len;//将数字转成字符串输入
    n=max(n,m);*/

    //for(int i=1;i<=n;i++)c[i]=a[i]...b[i];//...处为运算符号
    /*for(int i=1;i<=n;i++){
        c[i+1]+=c[i]/10;
        c[i]%=10;//模拟进位，以下被注释掉的大多也一样；
    }*/-----高精加法部分
    /*for(int i=1;i<=n;i++)
        if(c[i]<0){
            c[i]+=10;
            c[i+1]-=1;
        }

    while(c[n]==0)n-=1;*/-----高精减法部分

    /*for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            c[i+j-1] += a[i]*b[j];

    for(int i=1;i<=n+m-1;i++){
        c[i+1]+=c[i]/10;
        c[i]%=10;
    }
    n=n+m-1;
    while(c[n+1]>0)n+=1;*/-----高精乘法部分
    /*int B;
    cin>>B;
    cout<<B<<endl;
    for(int i=n;i>;i--){
        c[i]=a[i]/B;
        a[i-]+=(a[i]%B)*;
    }
    while(c[n]== && n>)n--;*/-----高精除以低精部分
    for(int i=n;i>;i--)printf("%d",c[i]);

}

•那么，负数怎么办呢？

其实可以分三种

（1）加法：

一个数是负数：变为减法；

两个数是负数：全部变成正数算加法，最后取负；

（2）减法：

被减数是负数：全部变为正整数算加法，最后取负

减数是负数：减数取负，变为加法

都是负数：都取负，变为减法，即（-减数）-（-被减数）

（3）乘除法：

统计负数个数s

都变为非负数计算，若s为奇数，最后取负

二、模意义下运算

•以七为例，模7意义下的运算：

（1）加法：         4 + 5 = 2  （4 + 5 = 9 = 7 * 1 + 2）

（2）减法：         4 - 5 = 6   （4 - 5 = - 1 = 7 * 1 - 6）

（3）乘法：         3 * 3 = 2   （3 * 3 = 9 = 1 * 7 + 2）

（4）除法：         3 / 3 = 1    （3 / 3 = 1 = 0 * 7 + 1）

（5）良心发现：          模意义下没有除法   ---蛤蛤蛤---

•模意义下运算的性质：

（1）满足基本的交换律、分配律、结合律

（2）对中间结果取模不影响最终答案

例：5 * 5 * 5 mod 7

=（5 * 5 mod 7）* 5 mod 7

= 4 * 5 mod 7

= 20 mod 7

= 6

• 快速幂：

题目描述：计算a ^ b % p = ?

三种思路：

（1）暴力（不说了，太难）

（2）分治

（3）神奇的快速幂（当做模板来记得了）

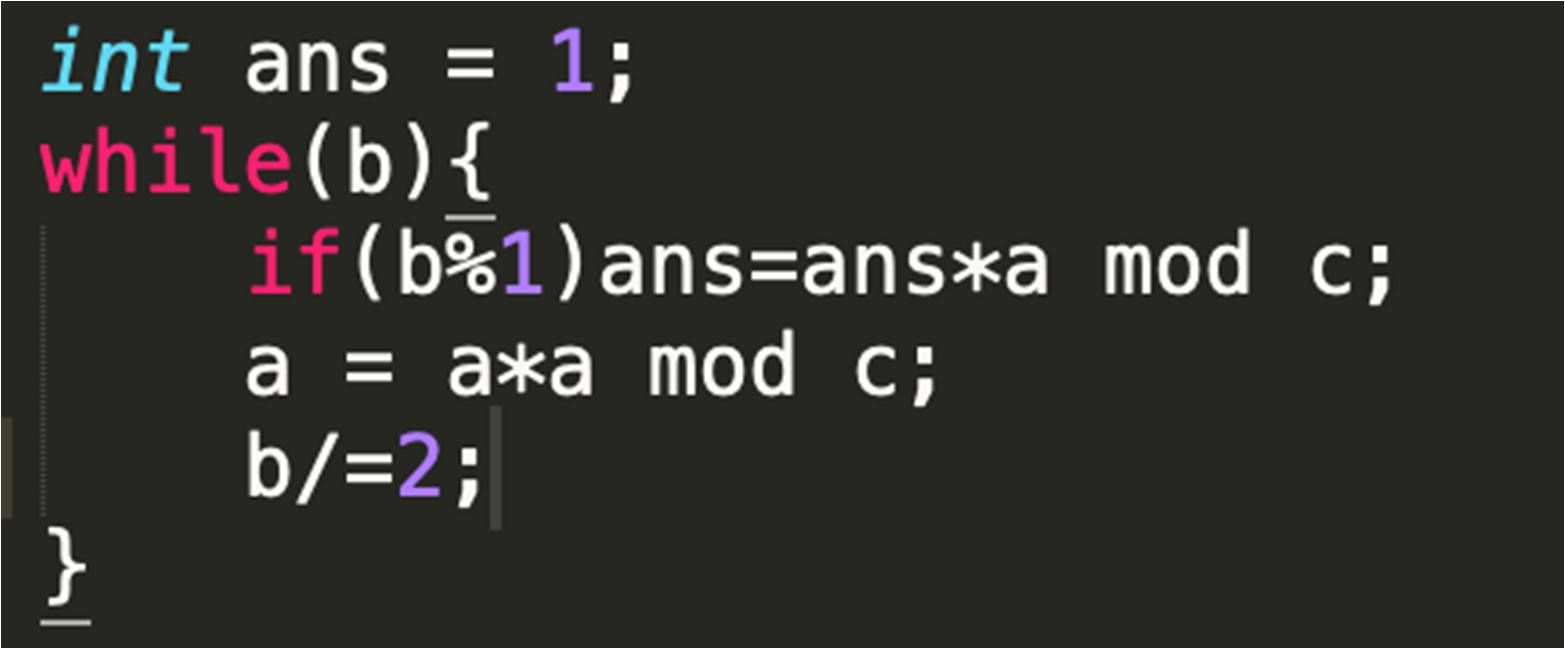
•费马小定理：

（1）定义：

对于素数p和任意正整数a（0~p-1），有a ^ (p-1) ≡ 1（mod p）

（2）应用：

计算C（n，m） % 10^ + 7

解：

C ( n , m ) = n ! / ( ( n - m ) !  * m ! )

= n ! * ( ( n - m ) ! * m ! ) ^ ( p - 2 )

= n ! * ( ( n - m ) ! ) ^ ( p - 2 ) * ( m ! ) ^ ( p - 2 )

•最大公约数

（1）一个叫gcd的东西

（2）gcd ( a , b ) = gcd ( b , a mod b )

（3）

•最小公倍数

（1）一个叫李春梅lcm的东西

（2）lcm ( a , b ) = a * b / gcd ( a, b )

（3）

•质数判别

（1）sqrt判别

（2）诶式筛

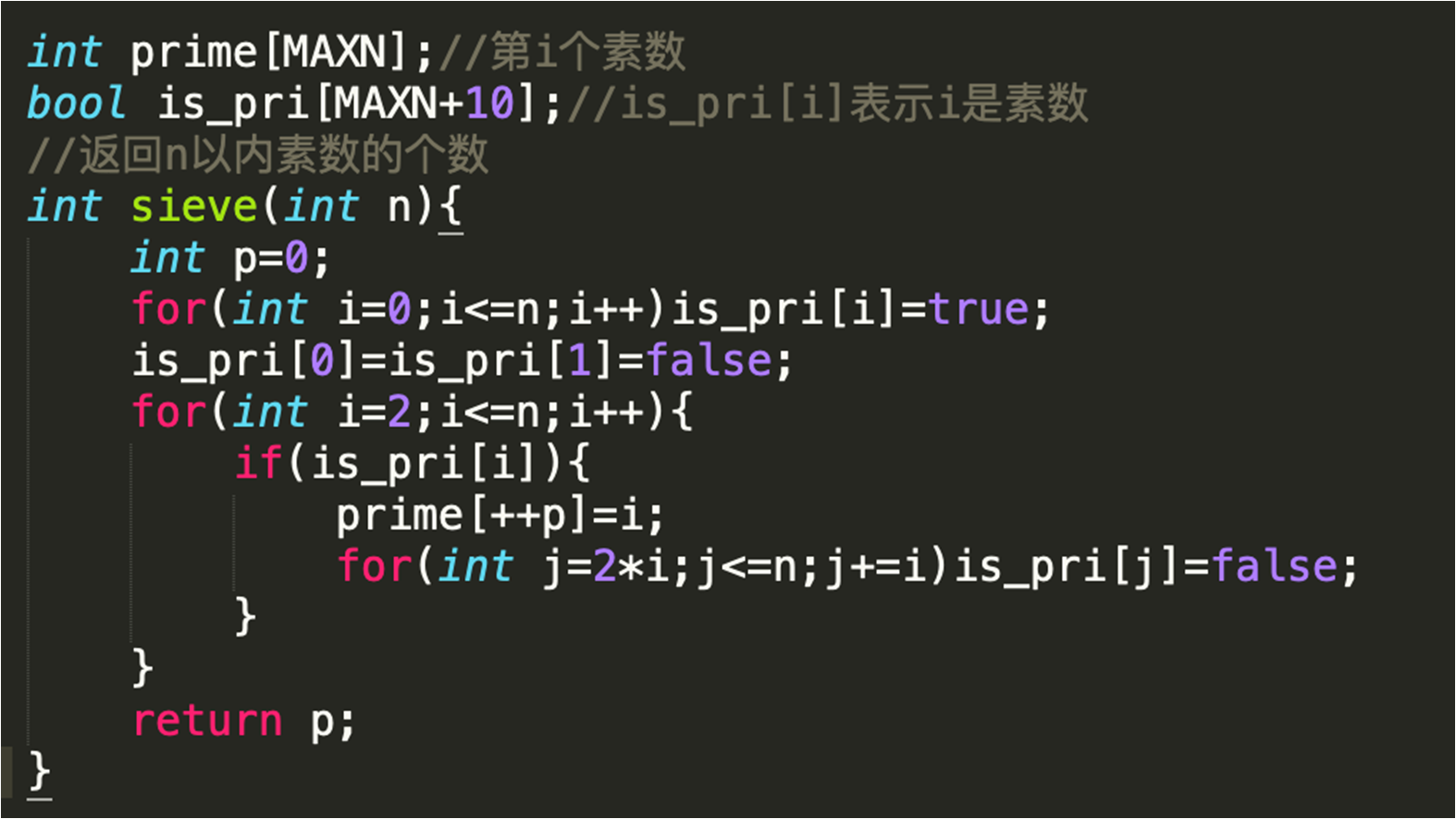
（3）线性筛

•欧拉函数

见选修4-6

下午篇

•蒟矩阵乘法

　　（1）一个m * n的矩阵就是m * n个数排列成m行n列的一个【数阵】

　　（2）一个m * p的矩阵A乘以一个p * n的矩阵B得到一个m * n的矩阵

　　（3）其中

　　　　（AB）ij=∑（k=1，p）aikbkj；

　　（4）图片描述

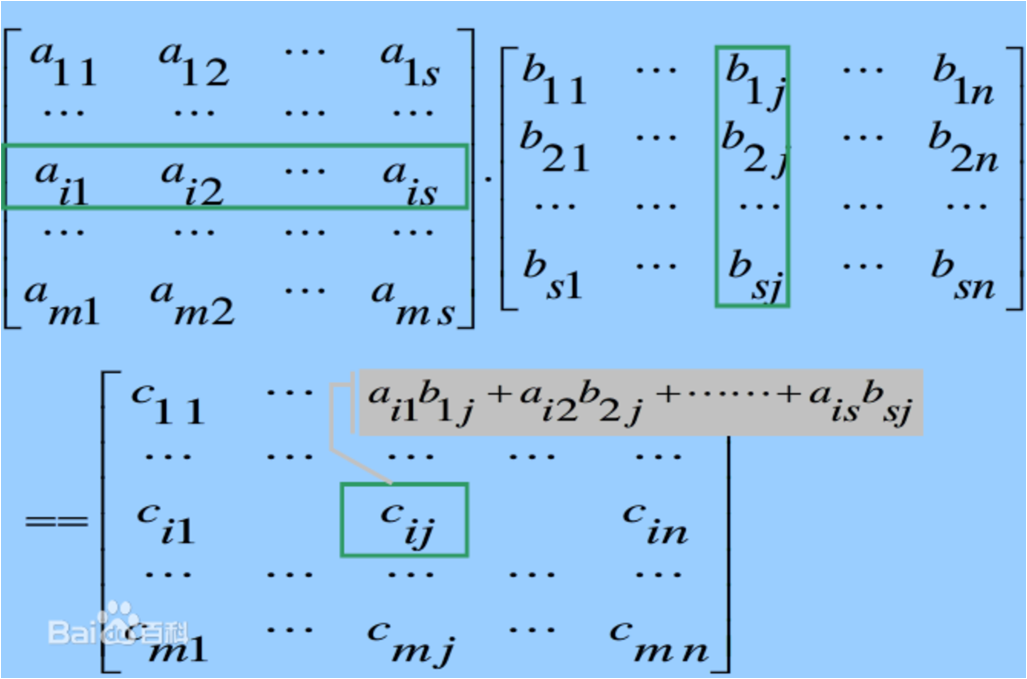
　　（5）例题

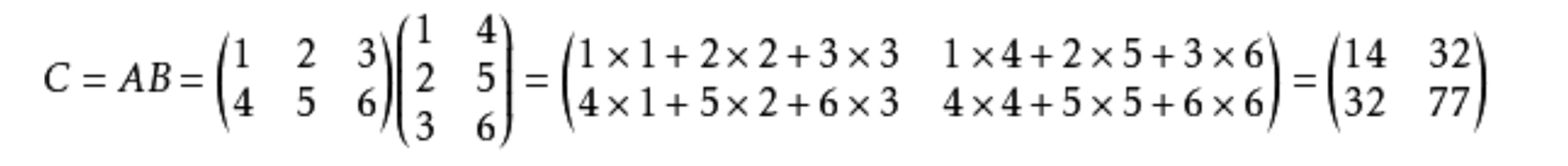
　　（6）注意：   矩阵乘法满足结合律、分配律，不满足交换律

　　（7）特殊矩阵的矩阵乘法：

　　　　　　上三角矩阵

分块矩阵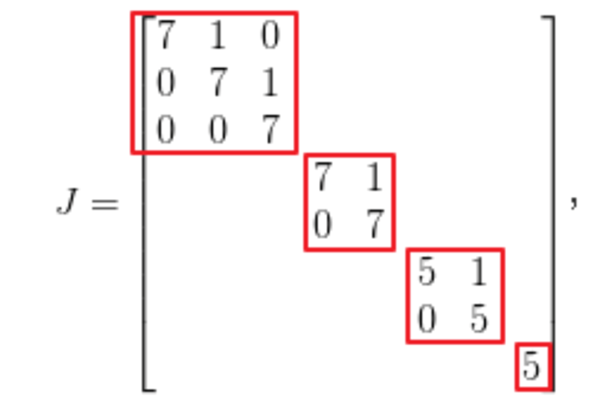

　　　　　　对角矩阵

　　　　　　对称矩阵

•行列式

　　（1）定义

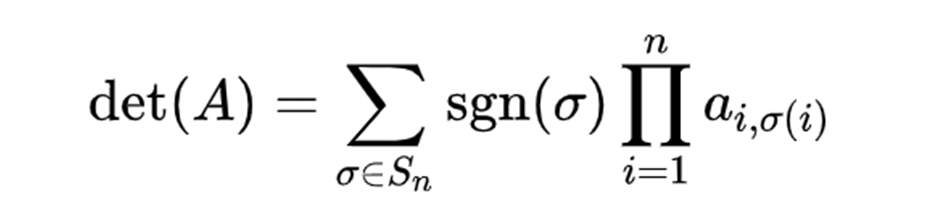
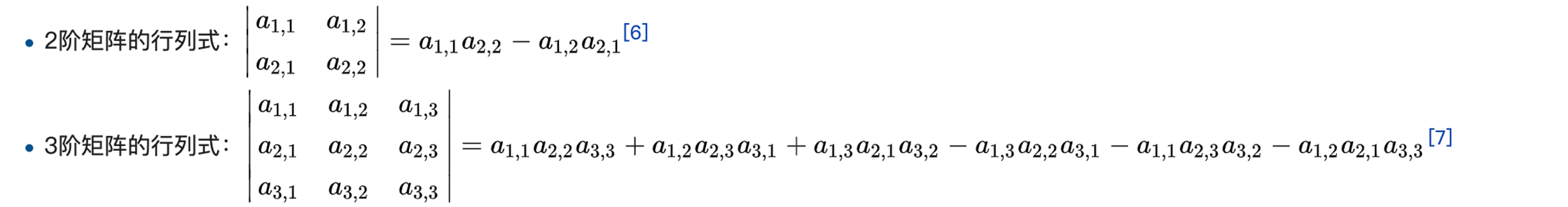
　　　　   哈哈其实是计算啦

　　（2）计算

•矩阵树定理

•有向图—矩阵树定理

***谢谢大家***