python数据结构之堆(heap)

本篇学习内容为堆的性质、python实现插入与删除操作、堆复杂度表、python内置方法生成堆。

区分堆(heap)与栈(stack)：堆与二叉树有关，像一堆金字塔型泥沙；而栈像一个直立垃圾桶，一列下来。

堆(heap)

又被为优先队列(priority queue)。尽管名为优先队列，但堆并不是队列。回忆一下，在队列中，我们可以进行的限定操作是dequeue和enqueue。

dequeue是按照进入队列的先后顺序来取出元素。而在堆中，我们不是按照元素进入队列的先后顺序取出元素的，而是按照元素的优先级取出元素。

性质

堆的实现通过构造二叉堆（binary heap），实为二叉树的一种；由于其应用的普遍性，当不加限定时，均指该数据结构的这种实现。这种数据结构具有以下性质。

• 任意节点小于（或大于）它的所有后裔，最小元（或最大元）在堆的根上（堆序性）。
• 堆总是一棵完全树。即除了最底层，其他层的节点都被元素填满，且最底层尽可能地从左到右填入。

实现

• 堆的主要操作是插入和删除最小元素(元素值本身为优先级键值，小元素享有高优先级)
• 在插入或者删除操作之后，我们必须保持该实现应有的性质: 1. 完全二叉树 2. 每个节点值都小于或等于它的子节点

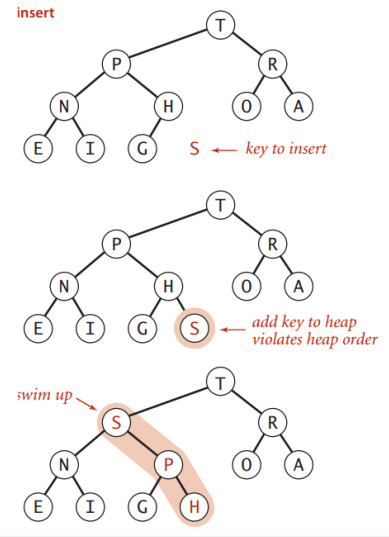
上浮（Promotion）

情境: 子节点的键值变为比父节点的键值大；如下面添加字节点

消除这种违反项：

• 交换子节点的键和父节点的键
• 重复这个过程直到堆的顺序恢复正常

堆的添加：

def _upheap(self, j):#往上交换
        parent = self._parent(j)
        if j > 0 and self._data[j] < self._data[parent]:
            self._swap(j, parent)
            self._upheap(parent) 

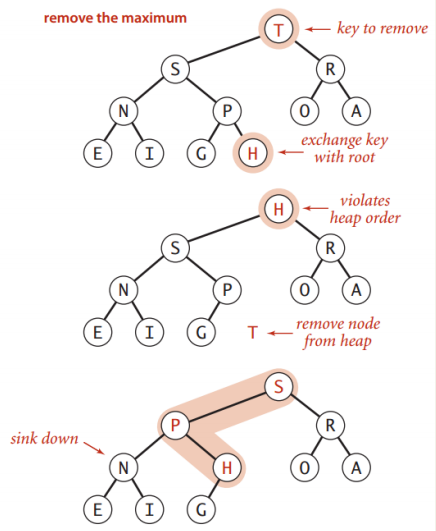
下沉（Demotion）

情境：父节点的键值变得比子节点（一个或者2个） 的键值还小 ，如下面删除了根节点后拿了个小子节点补充上来的情况

消除这种违反项：

• 把父节点的键值和比它大的子节点的键值做交换
• 重复这个操作直到堆的顺序恢复正常

删除最大值

def _downheap(self, j):#往下交换，递归比较三个值
        if self._has_left(j):
            left = self._left(j)
            small_child = left
            if self._has_right(j):
                right = self._right(j)
                if self._data[right] < self._data[left]:
                    small_child = right
            if self._data[small_child] < self._data[j]:
                self._swap(j, small_child)
                self._downheap(small_child)

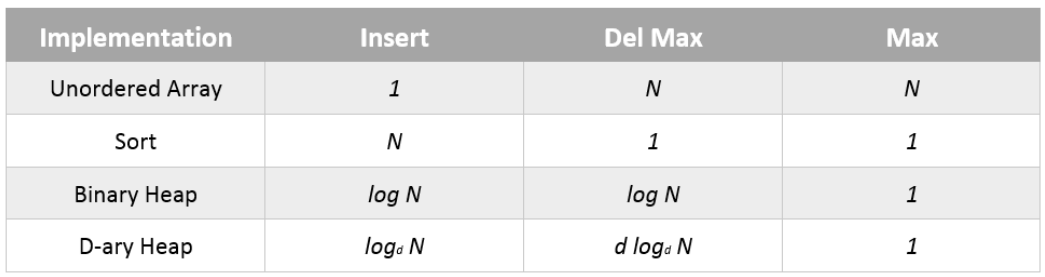
复杂度分析

Python构建堆的代码：

#该heap为min_heap，即根节点为最小值
class PriorityQueueBase:
    #抽象基类为堆

    class Item:
        #轻量级组合来存储堆项目
        __slots__ = '_key' , '_value'

        def __init__ (self, k, v):
            self._key = k
            self._value = v

        def __lt__ (self, other):     #比较大小
            return self._key < other._key

        def is_empty(self):
            return len(self) == 0   

        def __str__(self):
            return str(self._key)

class HeapPriorityQueue(PriorityQueueBase):

    def __init__ (self):
        self._data = [ ]         

    def __len__ (self):
        return len(self._data)

    def is_empty(self):
        return len(self) == 0  

    def add(self, key, value):   #在后面加上然后加上
        self._data.append(self.Item(key, value))
        self._upheap(len(self._data) - 1)

    def min(self):
        if self.is_empty():
            raise ValueError( "Priority queue is empty." )
        item = self._data[0]
        return (item._key, item._value)

    def remove_min(self):
        if self.is_empty():
            raise ValueError( "Priority queue is empty." )
        self._swap(0, len(self._data) - 1)
        item = self._data.pop( )
        self._downheap(0)
        return (item._key, item._value)

    def _parent(self, j):
        return (j - 1) // 2

    def _left(self, j):
        return 2 * j + 1

    def _right(self, j):
        return 2 * j + 2

    def _has_left(self, j):
        return self._left(j) < len(self._data)

    def _has_right(self, j):
        return self._right(j) < len(self._data)      

    def _swap(self, i, j):
        self._data[i], self._data[j] = self._data[j], self._data[i]

    def _upheap(self, j):#往上交换
        parent = self._parent(j)
        if j > 0 and self._data[j] < self._data[parent]:
            self._swap(j, parent)
            self._upheap(parent) 

    def _downheap(self, j):#往下交换，递归比较三个值
        if self._has_left(j):
            left = self._left(j)
            small_child = left
            if self._has_right(j):
                right = self._right(j)
                if self._data[right] < self._data[left]:
                    small_child = right
            if self._data[small_child] < self._data[j]:
                self._swap(j, small_child)
                self._downheap(small_child)  

heap = HeapPriorityQueue()
heap.add(4, "D")
heap.add(3, "C")
heap.add(1, "A")
heap.add(5, "E")
heap.add(2, "B")
heap.add(7, "G")
heap.add(6, "F")
heap.add(26, "Z")

for item in heap._data:
    print(item)

print("min is: ")
print(heap.min())
print()

print("remove min: ")
print(heap.remove_min())
print("Now min is: ")
print(heap.min())
print()

print("remove min: ")
print(heap.remove_min())
print("Now min is: ")
print(heap.min())
print()

heap.add(1, "A")
print("Now min is: ")
print(heap.min())
print()

#输出结果
1
2
3
5
4
7
6
26
min is:
(1, 'A')

remove min:
(1, 'A')
Now min is:
(2, 'B')

remove min:
(2, 'B')
Now min is:
(3, 'C')

Now min is:
(1, 'A')

python内置方法创建堆有两种方式，heappush()和heapify()

'''
heaqp模块提供了堆队列算法的实现，也称为优先级队列算法。
要创建堆，请使用初始化为[]的列表，或者可以通过函数heapify（）将填充列表转换为堆。
提供以下功能：
heapq.heappush（堆，项目）
将值项推入堆中，保持堆不变。
heapq.heapify（x）
在线性时间内将列表x转换为堆。
heapq.heappop（堆）
弹出并返回堆中的最小项，保持堆不变。如果堆是空的，则引发IndexError。
'''
import heapq 

#1 heappush生成堆+ heappop把堆从小到大pop出来
heap = []
data = [1,3,5,7,9,2,4,6,8,0]
for i in data:
    heapq.heappush(heap,i)
print(heap)

lis = []
while heap:
    lis.append(heapq.heappop(heap))
print(lis)

#2 heapify生成堆+ heappop把堆从小到大pop出来
data2 = [1,5,3,2,9,5]
heapq.heapify(data2)
print(data2)

lis2 = []
while data2:
    lis2.append(heapq.heappop(data2))
print(lis2)

#输出结果
[0, 1, 2, 6, 3, 5, 4, 7, 8, 9]
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
[1, 2, 3, 5, 9, 5]
[1, 2, 3, 5, 5, 9]