运用Turtle实现汉诺塔的可视化运行（递归算法）

运用Turtle实现汉诺塔的可视化运行（递归算法）

汉诺塔问题又名河内塔问题，是源于印度一个古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。

由题意得，此问题需要运用递归算法解决。

现在我们运用递归算法来解决汉诺塔

运行代码如下：

def good(n,a,b,c):
    if n==1:            #当只有一个盘子时
        print(a,'-->',c)#直接将其从A柱移至C柱
    else:               #当有n个盘子时
        good(n-1,a,c,b) #将上面n-1个盘子从A柱移至B柱
        print(a,'-->',c)#然后将A柱最底的盘子移至C柱
        good(n-1,b,a,c) #最后将n-1个盘子从B柱移至C柱
num = eval(input())
good(num,'A','B','C')

我输入：5

结果如图：

以上便是运用算法解决部分汉诺塔问题。当然，我们也可以将汉诺塔变为可视化，这就需要借助turtle库来实现。

我们可以运用turtle库来“画”出三个柱子，n个盘子。然而最困难的地方是要实现盘子在柱子之间的移动，根据我们现在所学知识有限，我们可以通过上网查询资料来了解与学习。

编写代码：

import turtle

class Stack:
    def __init__(self):
        self.items = []
    def isEmpty(self):
        return len(self.items) == 0
    def push(self, item):
        self.items.append(item)
    def pop(self):
        return self.items.pop()
    def peek(self):
        if not self.isEmpty():
            return self.items[len(self.items) - 1]
    def size(self):
        return len(self.items)

def drawpole_3():#画出汉诺塔的poles
    t = turtle.Turtle()
    t.hideturtle()
    def drawpole_1(k):
        t.up()
        t.pensize(10)
        t.speed(100)
        t.goto(250*(k-1), 100)
        t.down()
        t.goto(250*(k-1), -100)
        t.goto(250*(k-1)-20, -100)
        t.goto(250*(k-1)+20, -100)
    drawpole_1(0)#画出汉诺塔的polesA
    drawpole_1(1)#画出汉诺塔的polesB
    drawpole_1(2)#画出汉诺塔的polesC

def creat_plates(n):#制造n个盘子
    plates=[turtle.Turtle() for i in range(n)]
    for i in range(n):
        plates[i].up()
        plates[i].hideturtle()
        plates[i].shape("square")
        plates[i].shapesize(1,9-i)
        plates[i].goto(-250,-90+20*i)
        plates[i].showturtle()
    return plates

def pole_stack():#制造poles的栈
    poles=[Stack() for i in range(3)]
    return poles

def moveDisk(plates,poles,fp,tp):#把polesA顶端的盘子plates[mov]从polesA移到polesC
    mov=poles[fp].peek()
    plates[mov].goto((fp-1)*250,150)
    plates[mov].goto((tp-1)*250,150)
    l=poles[tp].size()        #确定移动到底部的高度（恰好放在原来最上面的盘子上面）
    plates[mov].goto((tp-1)*250,-90+20*l)

def moveTower(plates,poles,height,fromPole, toPole, withPole):#递归放盘子
    if height >= 1:
        moveTower(plates,poles,height-1,fromPole,withPole,toPole)
        moveDisk(plates,poles,fromPole,toPole)
        poles[toPole].push(poles[fromPole].pop())
        moveTower(plates,poles,height-1,withPole,toPole,fromPole)

myscreen=turtle.Screen()
drawpole_3()
n=int(input("请输入汉诺塔的层数并回车:\n"))
plates=creat_plates(n)
poles=pole_stack()
for i in range(n):
    poles[0].push(i)
moveTower(plates,poles,n,0,2,1)
myscreen.exitonclick()

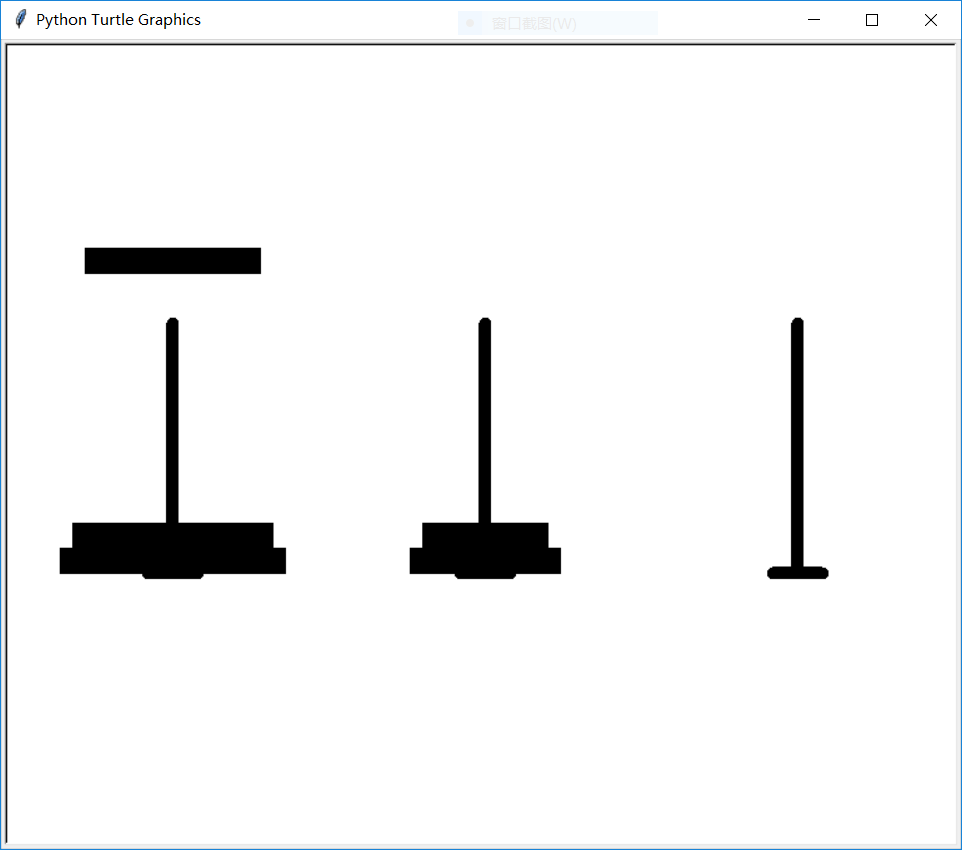
我们尝试五个盘子，输入：5

运行过程：

最后结果：（很遗憾不能使用动图）

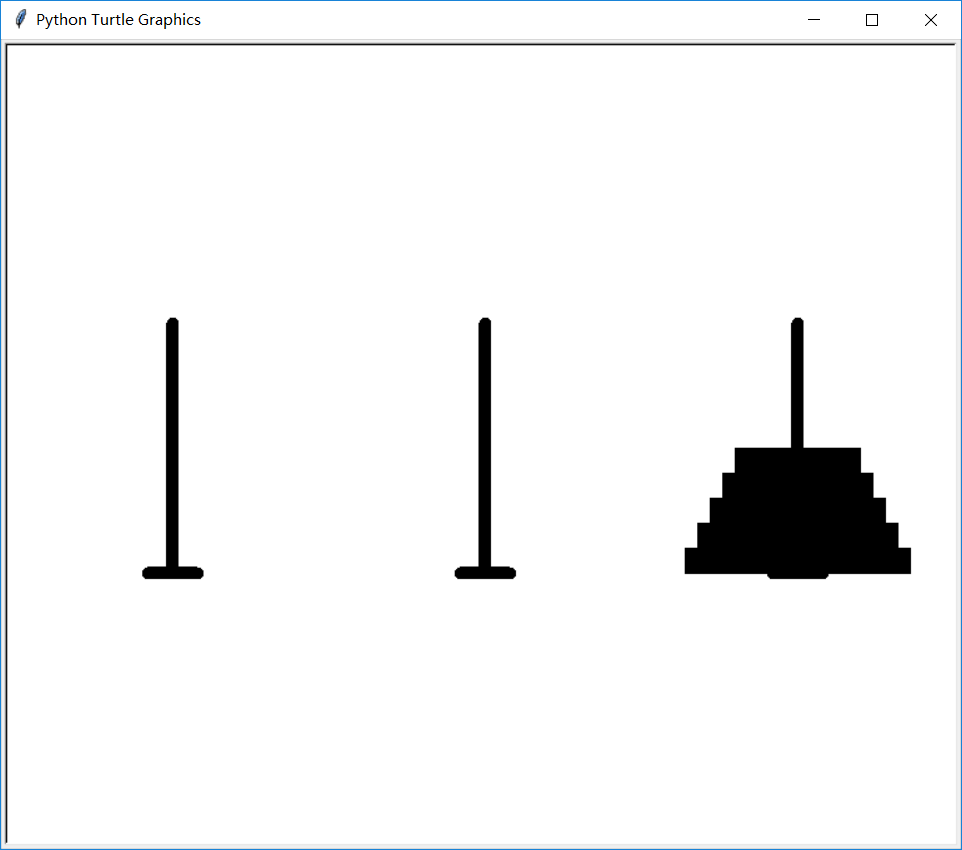
这个就是汉诺塔的可视化运行，当然我们还可以尝试更多的盘子，可能需要运行时间会更长。

今天又通过Python解决一个问题，开心~