Matlab_spectrogram_短时傅里叶分析_实现与讨论

在语音与音乐处理过程中，常用到短时傅里叶变换（Short Time Fourier Transformation, STFT）。在一些学习路径中，STFT也是学习小波之前的预备知识。本文简单实现了 Matlab 中 Spectrogram 函数，在没有小波知识支撑下，讨论了参数的选择，以及分辨率相关的问题。

参考博客：

　　来源：CSDN    作者：风翼冰舟
　　来源：知乎       作者：咚懂咚懂咚
　　来源：CSDN    作者：水可马二   　来源：CSDN    作者：沈子恒   　来源：CSDN    作者：gent__chen

短时傅里叶变换简介

---

　　自己写一下对STFT的认识，不一定对。

　　短时傅里叶变换，其实还是傅里叶变换，只不过把一段长信号按信号长度（nsc）、重叠点数（nov）重新采样。原始信号的每一个数据点，都有一个电压值对应，即只有一个直流自由度。重新采样之后，数据点个数变少，每一个数据点由（nsc）个点组成，即得到了其他频率的自由度。但是这个点的频谱是有上下限的——上限受采样频率界定，下限受数据时长界定，和 FFT 一样。

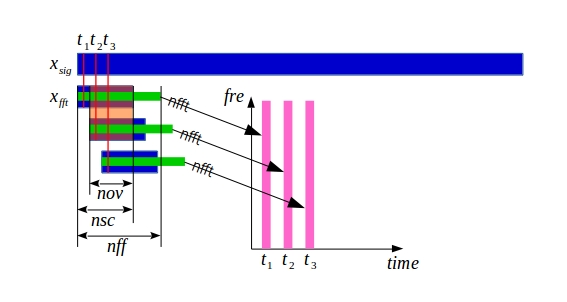
　　这么处理数据是有缘由的。语音与音乐信号中，信号频率常常变化，而且频率成分丰富，导致简单的傅里叶变换不能很好的描述信号。然而我们人耳处理声音的能力很强，可以对很短的一段声音进行精确的频率分析。所以在语音识别以及语音信号预处理过程中，STFT 是 FFT 的仿生改良版（个人理解）。当然，在其他声学相关方向中，STFT也是蛮有用的。没查过相关文献不敢乱说，模态分析、瞬态特性等应该能用上（个人猜测）。

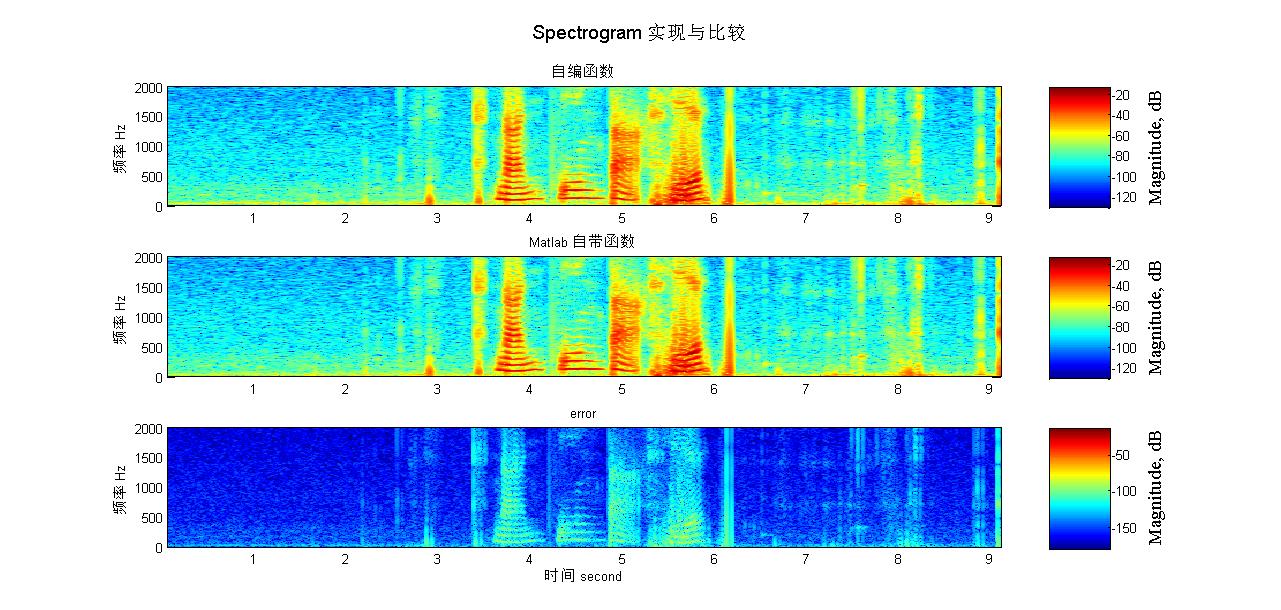
上图是我用本文的例程实现的语音“XX大学”的 STFT 结果。语音是自己拿录音笔录的，时间域上没有做截断，但由于自己声线太低，频率域截到 2000 Hz。可以看到，我在开始之后等了一段时间才开始说话，后面有几段“嘎嘣脆”的噪声。还可以看到，我的元音发音还是很清晰的，但声线真心低。理论上能从这张图还原出原始信号，不在话下。

Spectrogram 函数函数实现

---

　　简单编了一个 STFT 函数如下：

function [ S , W , T ] = mf_spectrogram...
    ( signal , nsc , nov , fs )
%MF_SPECTROGRAM Short-time Fourier transform realization
% Input
%       signal      - Signal vector
%       nsc         - Abb. of Number SeCtion
%       nov         - Abb. of Number OverLap
%       fs          - Abb. of Frequency of Sample
% Output
%       S           - A matrix that each colum is a FFT for time of nsc
%       W           - A vector labeling frequency
%       T           - A vector labeling time

  % Signal Preprocessing
    h = hamming(nsc, 'periodic');   % Hamming weight function
    L = length(signal);             % Length of Signal
    nst = nsc-nov;                  % Number of STep per colum
    ncl = fix( (L-nsc)/nst ) + 1;   % Number of CoLum
    nff = 2^nextpow2(nsc);          % Number of Fast Fourier Transformation
    Ps = zeros(nsc,ncl);
    for n = 1:ncl                   % Ps means Processed Signal
        Ps(:,n) = signal( (n-1)*nst+1 : (n-1)*nst+nsc ).*h';
    end                             % Ps is a matrix

  % Short-time Fourier transform
    STFT0 = fft(Ps,nff);

  % Turn into DFT in dB
    STFT1 = abs(STFT0/nff);
    STFT2 = STFT1(1:nff/2+1,:);             % Symmetric results of FFT
    STFT2(2:end-1,:) = 2*STFT2(2:end-1,:);  % Add the value of the other half
    STFT3 = 20*log10(STFT2);                % Turn sound pressure into dB level

  % Axis Generating
    fax = fs*(0:(nff/2))/nff;                           % Frequency axis setting
    tax = ( .5*nsc : nst : nst*(ncl-1)+.5*nsc ) / fs;   % Time axis generating
    [ffax,ttax] = meshgrid(tax,fax);                    % Generating grid of figure

  % Output
    W = ffax;
    T = ttax;
    S = STFT3;
end

　　为了节省代码量，我搞了一个绘图函数：

function [  ] = my_pcolor( f , t , s )
%MY_PCOLOR 绘图函数
% Input
%       f               - 频率轴矩阵
%       t               - 时间轴矩阵
%       s               - 幅度轴矩阵
    gca = pcolor(f,t,s);                      % 绘制伪彩色图
        set(gca, 'LineStyle','none');         % 取消网格，避免一片黑
    handl = colorbar;                         % 彩图坐标尺
        set(handl, 'FontName', 'Times New Roman', 'FontSize', 14)
        ylabel(handl, 'Magnitude, dB')        % 坐标尺名称
end

　　下面是实现的例程：

clc
clear
close all

% 基本参数
fa = [ 50 800 ];    % 扫描频率上下限
fs = 6400;          % 采样频率

% 分辨率相关设定参数
te = 1;             % [s] 扫频时间长度
fre = 8;            % [s] 频率分辨率
tre = 0.002;        % [Hz] 时间分辨率

% Chirp 信号生成
t = 0:1/fs:te;                  % [s] 时间序列
sc = chirp(t,fa(1),te,fa(2));   % 信号生成

% 分辨率相关输入参数
nsc = floor(fs/fre);
% nov = floor(nsc-(fs*tre));
nov = floor(nsc*0.9);
nff = max(256,2^nextpow2(nsc));

% 计算与绘制结果
subplot(1,3,1)                            % 绘制自编函数结果
    [S,W,T] = mf_spectrogram(sc,nsc,nov,fs);
    my_pcolor(W,T,S)
    caxis([-130.86,-13.667]);
    title('自编函数');
    xlabel('时间 second');
    ylabel('频率 Hz');
subplot(1,3,2)                            % 绘制 Matlab 函数结果
    s = spectrogram(sc,hamming(nsc),nov,nff,fs,'yaxis');
        % Turn into DFT in dB
        s1 = abs(s/nff);
        s2 = s1(1:nff/2+1,:);             % Symmetric results of FFT
        s2(2:end-1,:) = 2*s2(2:end-1,:);  % Add the value of the other half
        s3 = 20*log10(s2);                % Turn sound pressure into dB level
    my_pcolor(W,T,s3 )
    caxis([-130.86,-13.667]);
    title('Matlab 自带函数');
    xlabel('时间 second');
    ylabel('频率 Hz');
subplot(1,3,3)                            % 两者误差
    my_pcolor(W,T,20*log10(abs(10.^(s3/20)-10.^(S/20))))
    caxis([-180,-13.667]);
    title('error');
    ylabel('频率 Hz');
    xlabel('时间 second');
suptitle('Spectrogram 实现与比较');

　　跑的结果我就不贴了，Demo确定是没问题的。网上也有很多相关话题的，例程都比较简单，但我非常善于把问题复杂化：te（扫描长度）、fre（频率下限）、tre（时域分辨率）、nsc（单段数据长度）、nov（重叠数据点数）、nff（FFT点数） 等参数都是为了看设定什么样的参数能够使得 STFT 结果最优。我只是科普性地了解过小波，公式推导还没展开，所以在此只能“实验性”地讨论“尺度”相关的话题。

　　观察频率上限受到采样频率限制，频率下限受到nsc限制。nsc越大，单段数据时间跨度越长，在该段时间内频率如果变化快，会导致频域分辨率降低（te = 1 ; fre = 2 ; nov = 99%）。另一方面，为了保持 FFT 频率分辨率，设置 nff 不低于256，这使得当nsc较小时，单段信号中，低频成分可能也就几个周期就结束了，等同于时域加了一个矩形窗，最终造成了频域产生旁瓣。一句话，单段信号过短，低频效果不好；单段信号过长，捕捉不到频率快速变化的信号。

数据长度、FFT 点数对结果的影响

---

　　实验性地比较了一下不同数据长度、FFT点数对结果的影响：

%  This script is demonstrating zero effects
% Basic parameter
fs = 100;                   % 采样频率
Ndata = [ 30 60 500 ];          % 数据长度
Nff = [ 32 64 512 ];        % FFT的数据长度

% Signal Generating
t1 = ( 0:Ndata(1)-1 )/fs;
t2 = ( 0:Ndata(2)-1 )/fs;
t3 = ( 0:Ndata(3)-1 )/fs;
x1 = 0.5*sin(2*pi*15*t1)+2*sin(2*pi*40*t1);        % 时间域信号
x2 = 0.5*sin(2*pi*15*t2)+2*sin(2*pi*40*t2);        % 时间域信号
x3 = 0.5*sin(2*pi*15*t3)+2*sin(2*pi*40*t3);        % 时间域信号

% FFT and Plot
for n = 1:3             % Ndata sweep
    xname = ['x',num2str(n)];
    x = eval(xname);
    for m = 1:3         % Nff sweep
        name = ['y',num2str(n),num2str(m)];
        eval([name '=fft(x,Nff(m));'])
        y = eval(name);
        Y = abs(y);
        f = (0:Nff(m)-1)*fs/Nff(m);   % 真实频率

        subplot(3,3,(n-1)*3+m)
        plot(f(1:Nff(m)/2),[Y(1),Y(2:Nff(m)/2)*2]/min(Ndata(n),Nff(m)));
        xlabel('频率/Hz');
        ylabel('振幅');
        ylim([0,2]);
        title(['Ndata=',num2str(Ndata(n)),' Nfft=',num2str(Nff(m))]);
        grid on;
    end
end

为了节省代码，同时运行结束后保留计算数据，使用了 eval 函数对变量和字符串进行相互转化。绘制了9个图如下：

横向是提高 FFT 点数的比较，纵向是提高数据长度的比较。可以看到，提高 FFT 点数会使得频域分辨率提高；增长数据长度，能够减少旁瓣的生成。

---

END