多项式求导系列——OO Unit1分析和总结

一、摘要

　　本文是BUAA OO课程Unit1在课程讲授、三次作业完成、自测和互测时发现的问题，以及倾听别人的思路分享所引起个人的一些思考的总结性博客。本文第二部分介绍三次作业的设计思路，主要以类图的形式展现，并有简单的优劣分析；第三部分为程序代码复杂度的分析（二、三两部分为基于度量的对自己程序结构的分析）；第四部分为对自己、对他人程序的测试、DEBUG、Hack的思考；第五部分是分析作业中可以应用对象创建模式的可能性，和重构的思考。

二、开发设计思路

1.程序类图展示

第一次作业

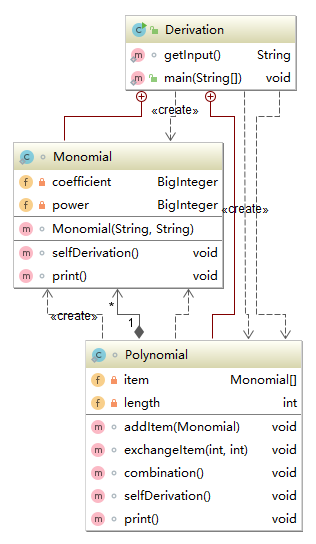
第二次作业

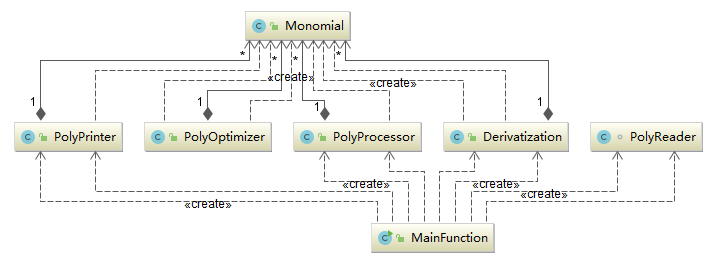
第三次作业

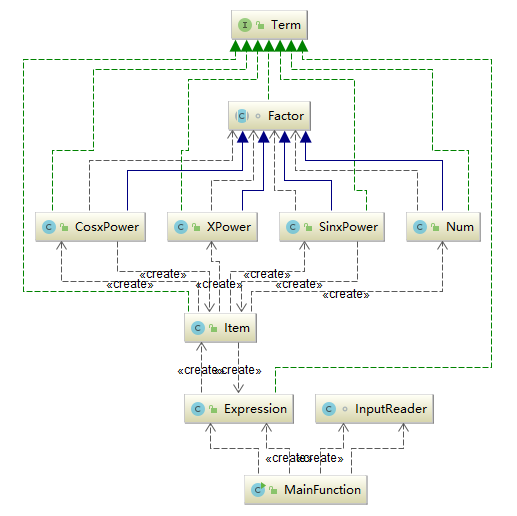
2.简单分析

　　这三次作业我基本上采用了完全不同的方法，感觉到其实非常有趣并且很有收获。

　　第一次作业的时候我的所有代码都在一个.class文件内，设计了一个没有什么意义的主类Derivation，包含了一个多项式类和一个单项式类。这种设计除了在文件管理上不容易丢失文件以外基本没有什么好处。第二次和第三次作业中代码才越来越面向对象。第三次中有一些体现抽象工厂的设计，使用了Factor接口和Item抽象类，显然第三次作业的程序更具有可扩展性。实际上我在第二次作业中就有意识地在降低模块的耦合以方便单元测试。

　　第二次和第三次的作业实际上采用了不同的设计思路，主要在于第二次是为了提高对输出优化处理的可扩展性，第三次是为了提高支持输入的项的类型的可扩展性。第二次中的对象保存的是对一个多项式的各种处理方法，而第三次的对象保存的是多项式的各种组成成分。这两个程序一个在怎么处理产品的方法上有较好扩展性，一个在能处理的产品种类上有较好扩展性。此外，第三次作业我尝试直接使用字符串来保存数据，无意中使用了Creative Pattern。前两次作业中，会牵涉到对象的拷贝等，容易发生错误，某些对象的方法可能不具有可再现性，引入不安全性并且不利于单元测试；第三次作业中，由于没有计划做详细的优化，使用了直接进行字符串操作的简化设计，但非常不利于优化。此外，前两次作业使用的容器还较为传统（定长数组），不利于利用现有的包进行合并同类项优化而自己写了优化的方法，虽然实现简单，但是也浪费了空间资源。

三、程序结构分析

1.度量分析

第一次作业

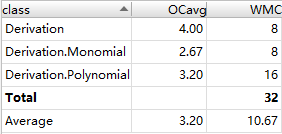
第二次作业

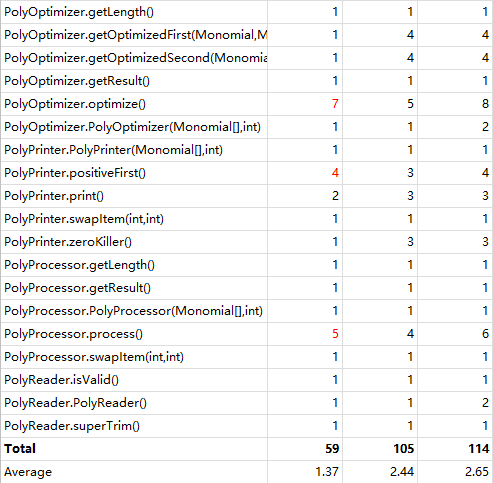
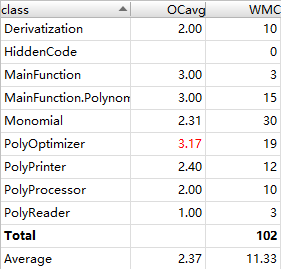
第三次作业

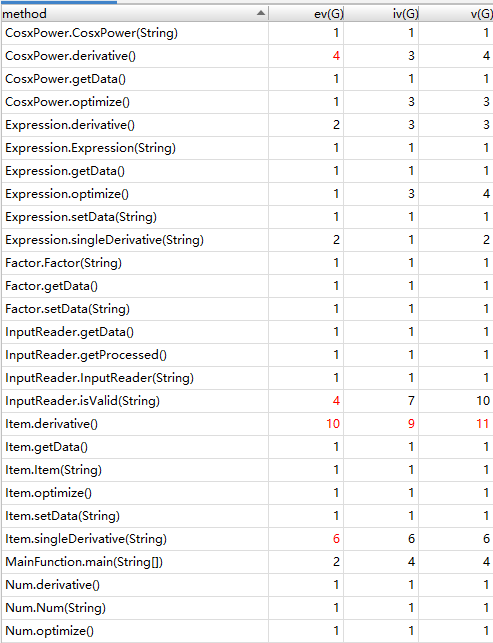
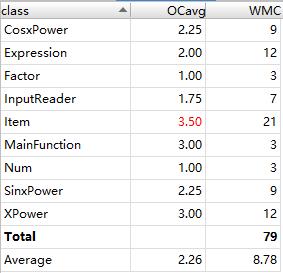
从三次作业来看，代码结构的基本复杂度、模块复杂度和圈复杂度呈现明显的逐次下降趋，体现出我的程序更加结构化、模块化，这有利于代码的理解和结构化、模块化的维护、测试和功能扩展；各模块之间耦合度降低，有利于模块的隔离、维护和复用；程序独立路径的数量也在减少，则出现错误的几率会降低，亦有利于测试和维护。

四、测试、DEBUG与互评

1.个人BUG分析

第一次作业：

• 引发错误的数据：“+x+x+x...”（大量“+x”构成的长输入）
• 引发的错误：正则表达式匹配栈溢出错误
• 没有测出的原因：本地使用JDK版本比评测机高，该版本正则表达式并不会发生这样的匹配导致栈溢出的错误，所以虽然本地也测试过这种数据，但是并不会引发错误
• 错误的代码：

   "|\\d+)[ \t]*)*[ \t]*";

• 修改后的代码：

123   "|\\d+)[ \t]*)*+[ \t]*";

• 分析：使用在匹配中使用独占模式即可使得程序在对整个输入进行匹配后不进行回溯，从而避免栈溢出的错误。

第二次作业：

• 引发错误的数据：“x^2*cos(x)^6*sin(x)^7+x*cos(x)^6*sin(x)^7”
• 引发的错误：优化时引入了计算错误
• 没有测出错误的原因：测试不充分
• 错误的代码：

     boolean canOptimizeWith(Monomial m) {
         return ((this.power.equals(m.power) &&
                 (this.sinPower.equals(
                         m.sinPower.add(new BigInteger("2")))
                        && m.cosPower.equals(
                         this.cosPower.add(new BigInteger("2"))))
                 || (this.cosPower.equals(
                 m.cosPower.add(new BigInteger("2")))
                 && m.sinPower.equals(this.sinPower.add(new BigInteger("2")))))));
      }

• 修改后的代码：

48         return (this.power.equals(m.power) &&

55                         this.cosPower.add(new BigInteger("2")))

• 分析：判断两项是否满足优化条件的方法错误，逻辑太复杂导致的括号错误。

第三次作业：

• 引发错误的数据：cos((-x^+7*x^7))^+1
• 引发的错误：对象调用了自己的方法导致循环调用，引发栈溢出错误
• 没有测试出的原因：测试不充分
• 错误的代码：

    public void optimize() {
        if (super.getData().matches(".*\\^0*1")) {
            setData(getData().replaceAll("\\^0*1", ""));
        } else if (super.getData().matches(".*\\^0*")) {
            setData("1");
        }
    }

• 正确的代码：

     public void optimize() {
         if (super.getData().matches(".*\\^0*1")) {
             setData(super.getData().replaceAll("\\^0*1", ""));
         } else if (super.getData().matches(".*\\^0*")) {
             setData("1");
        }
    }

• 分析：我的设计中getData时要优化，优化的时候要调用父类的getData，如果调用自己的，则会循环调用。

2.互测BUG分析和Hack技巧

　　我互测中遇到的BUG主要是对数据的输入处理的问题，例如未判断正负号使用是否正确就先去除了重复的正负号，或者在正则表达式中使用“\s”从而引入了不允许的特殊字符的可能性，或者某些位置应该允许输入多个空格只允许了单个。还有对不完整的输入，比如“+x+”,"45*"等没有进行判断。第三次作业中，还有同学没有使用BigInteger处理数据，或者对指数为000000000000000000001的输入进行了报错，说明这方面没有处理得当。还有对于如“x*+1”的乘法内含有带符号整数因子处理错误的情况。

　　主要通过阅读代码针对性测试和构造测试数据盲测结合进行测试。JUnit的Series能够排列组合生成一些数据，同学分享的随机生成字符串也能生成数据，但主要还是人工设计的边界条件数据或者特殊情况数据更容易测出错误。在时间允许的情况下，阅读代码是最有效的找到别人BUG的方法。当然，自己设计时积攒或出错过的测试数据也有使用的价值。

3.对提高DEBUG效率的思考

What Information	More Information	Less Information
Trail	Step by step	Conditional Breakpoints
Code	The whole code	Coverage
Value of variables	Variables	Watches/Evaluation
Exception	Throw an exception	...
Anything	Hiearchy +	Hiearchy -

　　我认为DEBUG也是值得思考的事情。DEBUG是根据提供的信息寻找所写代码中错误并改正的过程。通过IDEA和Eclipse所支持的丰富的功能，我们可以轻易的获得包括代码覆盖、变量值、代码轨迹等信息，通过增加和减少信息结合自己程序的设计结构，可以大大减少锁定bug的时间。利用条件断点实现分级的DEBUG信息输出也是有价值的DEBUG方法。

五、对象创建模式的应用思考

　　第一次作业中，我没有实现多项式类，将多项式当做多个单项式存储在数组中进行处理，并编写相应的各种方法。可以重构，设计多项式类，仅包含HashMap类，而且由于多项式求导后还是多项式，求导方法可以使用new的方法返回一个多项式。

　　第二次作业中，也没有实现多项式类。仍可设计多项式类，各种多项式处理器与主函数的数据交流也可以重构为对象创建的方法，每次返回一个new多项式，可以使得各种求导、优化、合并同类项、根据三角函数公式优化等方法可以独立地开发和测试。

　　第三次作业我已经有使用工厂模式的影子，仍有很多可以改进的地方。可以完成部分优化工作，这里就需要注意equals方法的重写以支持合并同类项。此外，在我设计中使用了替换字符以屏蔽括号内正负号和乘号的处理方法来应对多层嵌套，分割后再将字符换回，这个有很大的不安全性，也可以重构，将这种乘积和单项式匹配方法（即递归地根据+、*分割输入）改为expression tree对象的处理，改为工厂模式，可以减少正则表达式的使用和避免对输入数据的改动引起的不安全性。