图论之最短路径floyd算法

Floyd算法是图论中经典的多源最短路径算法，即求任意两点之间的最短路径。

它可采用动态规划思想，因为它满足最优子结构性质，即最短路径序列的子序列也是最短路径。

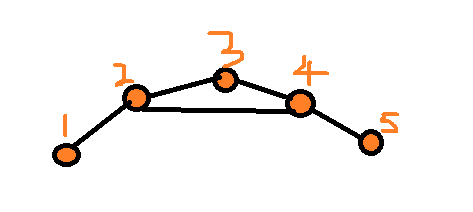
举例说明最优子结构性质，上图中1号到5号的最短路径序列<1,2,4,5>，其子序列<1,2,4>也是最短路径。

在动态规划算法中，处于首要位置、且也是核心理念之一的就是状态的定义。

动态转移的基本思想可以认为是建立起某一状态和之前状态的一种转移表示。

d[k][i][j]定义为“只能使用第1号到第k号点作为中间媒介时，点i到点j之间的最短路径长度”。

按照前面的定义，d[k][i][j]是一种使用1号到k号点的状态，可以想办法把这个状态通过动态转移，规约到使用1号到(k-1)号的状态，即d[k-1][i][j]。

对于d[k][i][j]（即使用1号到k号点中的所有点作为中间媒介时，i和j之间的最短路径），可以分为两种情况：

（I）i到j的最短路不经过k；

（II）i到j的最短路经过了k。

不经过点k的最短路情况下，d[k][i][j]=d[k-1][i][j]。

经过点k的最短路情况下，d[k][i][j]=d[k-1][i][k]+d[k-1][k][j]。

因此，综合上述两种情况，便可以得到Floyd算法的动态转移方程：

d[k][i][j] = min(d[k-1][i][j], d[k-1][i][k]+d[k-1][k][j])（k,i,j∈[1,n]）

在这里，需要注意上述动态转移方程的初始（边界）条件，即d[0][i][j]=w(i, j)，

也就是说在不使用任何点的情况下（“松弛操作”的最初），两点之间最短路径的长度就是两点之间边的权值。

方法：“松弛”点，“五行代码”通过n-1次松弛节点

参考资料：https://www.cnblogs.com/chenying99/p/3932877.html