The Problem of Overfitting

Cost Function

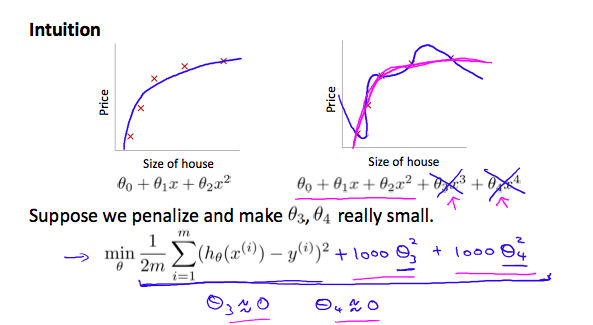
Regularized Linear Regression

Note: [8:43 - It is said that X is non-invertible if m ≤ n. The correct statement should be that X is non-invertible if m < n, and may be non-invertible if m = n.

We can apply regularization to both linear regression and logistic regression. We will approach linear regression first.

Regularized Logistic Regression

We can regularize logistic regression in a similar way that we regularize linear regression. As a result, we can avoid overfitting. The following image shows how the regularized function, displayed by the pink line, is less likely to overfit than the non-regularized function represented by the blue line:

Solving the Problem of Overfitting的更多相关文章

  1. machine learning(13) -- solving the problem of overfitting:regularization

    solving the problem of overfitting:regularization 发生的在linear regression上面的overfitting问题 发生在logistic ...

  2. 机器学习(四)正则化与过拟合问题 Regularization / The Problem of Overfitting

    文章内容均来自斯坦福大学的Andrew Ng教授讲解的Machine Learning课程,本文是针对该课程的个人学习笔记,如有疏漏,请以原课程所讲述内容为准.感谢博主Rachel Zhang 的个人 ...

  3. The first step in solving any problem is recognizing there is one.

    The first step in solving any problem is recognizing there is one.解决问题的第一步是要承认确实存在问题.

  4. 吴恩达机器学习笔记19-过拟合的问题（The Problem of Overfitting）

    到现在为止,我们已经学习了几种不同的学习算法,包括线性回归和逻辑回归,它们能够有效地解决许多问题,但是当将它们应用到某些特定的机器学习应用时,会遇到过拟合(over-fitting)的问题,可能会导致 ...

  5. 1763 An Essay towards solving a Problem in the Doctrine of Chances

    https://en.wikipedia.org/wiki/An_Essay_towards_solving_a_Problem_in_the_Doctrine_of_Chances

  6. Ng第七课：正则化与过拟合问题 Regularization/The Problem of Overfitting

    7.1  过拟合的问题 7.2  代价函数 7.3  正则化线性回归 7.4  正则化的逻辑回归模型 7.1  过拟合的问题 如果我们有非常多的特征,我们通过学习得到的假设预测可能能够非常好地适应训练 ...

  7. Machine Learning - 第3周（Logistic Regression、Regularization）

    Logistic regression is a method for classifying data into discrete outcomes. For example, we might u ...

  8. 《Machine Learning》系列学习笔记之第三周

    第三周 第一部分 Classification and Representation Classification 为了尝试分类,一种方法是使用线性回归,并将大于0.5的所有预测映射为1,所有小于0. ...

  9. Andrew Ng机器学习课程笔记--week3（逻辑回归&正则化参数）

    Logistic Regression 一.内容概要 Classification and Representation Classification Hypothesis Representatio ...

随机推荐

  1. 今日SGU 5.1

    SGU 100 题意: 普通的a+b #include<bits/stdc++.h> #define de(x) cout<<#x<<"="&l ...

  2. Resource Access Based on Multiple Credentials

    A collection of multiple user credentials each associated with one of multiple different users is ob ...

  3. PatentTips - Improving security in a virtual machine host

    BACKGROUND Computer viruses are a common problem for computer users. One typical mode of attack is t ...

  4. SNMP介绍，OID及MIB库

    http://blog.sina.com.cn/s/blog_4502d59c0101fcy2.html

  5. 如果笔记本的 WIN7 运行很卡，请尝试运行这些批处理

    如果笔记本的 WIN7 运行很卡,请尝试运行这些批处理 WIN7是不是很卡?关掉下列服务吧 @echo off rem AppXSvc 为部署应用商店应用程序提供基础结构支持 rem BITS 微软的 ...

  6. vue.js有什么用，是用来做什么的（整理）

    vue.js有什么用,是用来做什么的(整理) 一.总结 一句话总结:用数据绑定的思想,vue可以简单写单个页面,也可以写一个大的前端系统,也可以做手机app的界面. 1.Vue.js是什么? 渐进式框 ...

  7. error: function declaration isn’t a prototype [-Werror=strict-prototypes]

    "warning: function declaration isn't a prototype" was caused by the function like that:   ...

  8. HDU 1007 Quoit Design 平面内最近点对

    http://acm.hdu.edu.cn/showproblem.php?pid=1007 上半年在人人上看到过这个题,当时就知道用分治但是没有仔细想... 今年多校又出了这个...于是学习了一下平 ...

  9. BZOJ4182: Shopping(点分治，树上背包)

    Description 马上就是小苗的生日了,为了给小苗准备礼物,小葱兴冲冲地来到了商店街.商店街有n个商店,并且它们之间的道路构成了一颗树的形状. 第i个商店只卖第i种物品,小苗对于这种物品的喜爱度 ...

  10. CList 点击表头排序 （2）两种排序方法中其中一种

    上一篇讲解SortItem()方法如何使用,虽然都是抄别人的但是就是想让大家有个大概的了解 CList 点击表头排序 (1)SortItems函数 点击表头排序基本思路都是 1.首先响应HDN_ITE ...