RBM（受限玻尔兹曼机）和深层信念网络（Deep Brief Network）

目录：

• 一、RBM

• 二、Deep Brief Network

• 三、Deep Autoencoder

一、RBM

1、定义【无监督学习】

RBM记住三个要诀：1）两层结构图，可视层和隐藏层；【没输出层】2）层内无连接，层间全连接；3）二值状态值，前向反馈和逆向传播求权参。定义如下：

一般来说，可见层单元用来描述观察数据的一个方面或一个特征，而隐藏层单元的意义一般来说并不明确，可以看作特征提取层。

比较通俗解释RBM的博客：https://blog.csdn.net/u013631121/article/details/76652647

玻尔兹曼机的模型，它一共有两层：如下图，下边4个圈为可见层【即输入层】，上面3个圈为隐藏层。双向箭头【因为前向传播和后向传播，无监督学习】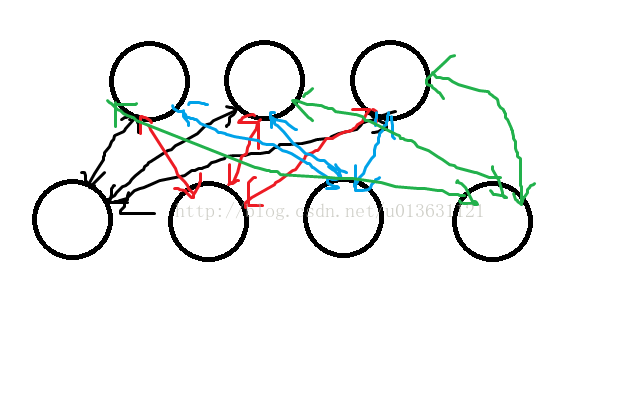

前向传播：

• b为偏置，如左上角的圈计算：y1=x1*w11+x2*w21+x3*w31+x4*w41+b1。将y1,y2,y3求出，加上激活函数即可。

• a为偏置。通过算出来的y1，y2，y3再回求一遍x1~x4。为了方便区分，回求的值我们叫做x‘1~x’4。举个例子求x'1，把隐含层3个数据与权值相乘，之后把偏置量a1给加上就完事儿了，公式写作x1=y1*w11+y2*w12+y3*w13+a1。其余3个也按照这个方式求出。
• 求完x‘1~x’4后用x‘1~x’4对隐含层再次求一遍值，得到y'1~y'3三个数。

反向传播：

目标函数：我们要做的就是让我们求得x与x'尽量相等，但是我们通过计算他们的差值，不为0，那怎么办呢，那就是反向传播。

权重计算：x和y的矢量做乘积，x'与y'做乘积，求出z与z'两个矩阵，这两个矩阵shape(x，y)，z与z'相减，然后加入到权值里面，例如w11，那么新的w11值就为：w11=w11+alpha*(z11-z'11)，alpha为学习速率，其它的权值也是一样计算。

偏置量计算：隐含层偏置量b1更新值为：b1=b1+alpha*(y1-y'1)，可视层偏置量a1=a1+alpha*(x1-x'1)，其余偏置量同理计算。

前向、后向传播迭代训练直到输入x和训练x'近乎相等。

前向、后向传播的例子解释：区分以下大象和狗的图。

正向更新：给定这些像素，权重应该送出一个更强的信号给大象还是狗？

反向更新：给定大象和狗，我应该送出一个什么样的像素分布？

2、RBM原理：

能量模型：一般认为物体的能量越高越不稳定，能量越低越趋于稳定。比如说，斜坡上的一个箱子，它位于越高的位置，则拥有更高的重力势能。能量模型把箱子停在哪个位置定义为一种状态，每个状态对应着一个能量。这个能量由能量函数来定义，箱子位于某个位置(某个位置)的概率。比如箱子位于斜坡1/2高度上的概率为p，它可以用E表示成p=f(E)。

RBM结构：

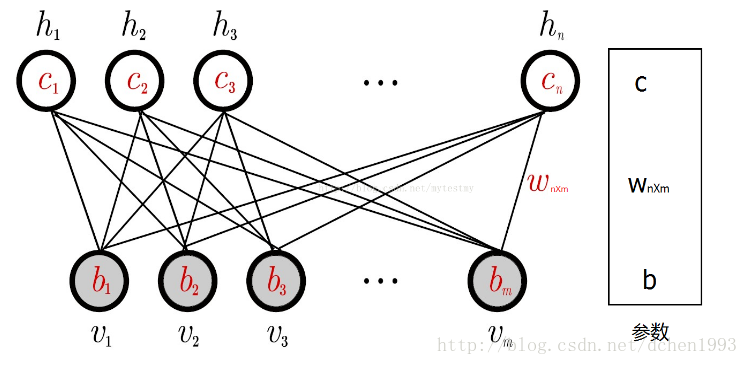
这里为了简单描述，假设每个节点的取值为{0,1}。

计算过程：

求解极大似然：梯度上升。参考http://lib.csdn.net/article/deeplearning/59097?knId=1746

二、 Deep Brief Network概念：多个Restricted Boltlzmann Machines

通俗解释：深度信念网络就是指能够通过概率大小学习的神经网络。把RBM堆叠在一块，然后形成一大串连接的RBM，最后在顶端加入一个输出层，就是深度信念神经网络。

如图：

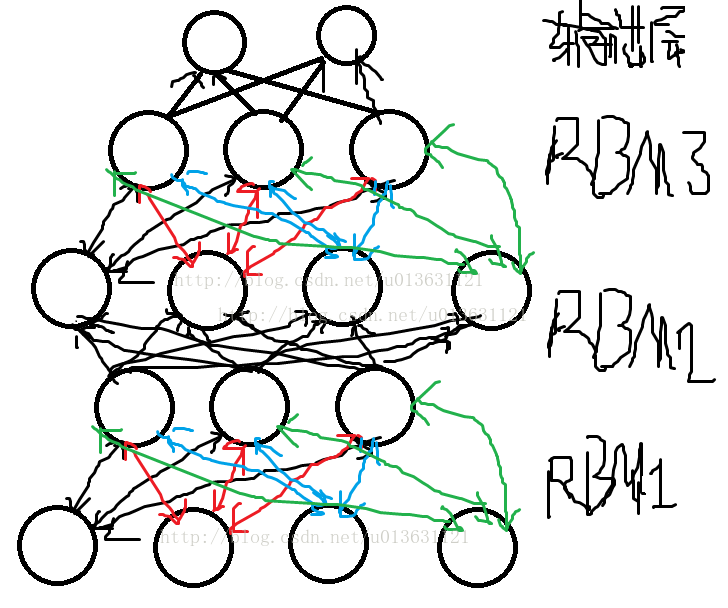
运行图：就是把原始数据输入到最下面的RBM可视层中，然后训练RBM1，训练完成之后把RBM1的隐含层作为RBM2的可视层，继续训练RBM2，接下来把RBM2的隐含层做为RBM3的可视层，直到训练完成为止。

每层的神经元不与本层的其他神经元交流。最后一层通常是分类层（eg,softmax)

除了第一层和最后一层，每层都有两个作用：对于前一层作为隐藏层，作为后一层的输入层。

三、Deep Autoencoders：有两个Deep Brief Network组成

自编码作用：用来降低维度，图像搜索（压缩），数据压缩，信息检索

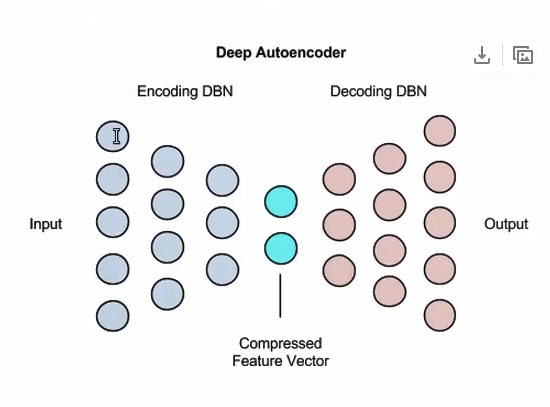
下图：中间蓝色：相当于学习到的特征向量，左边为自编码，右边为解编码。

每层由RBM组成。