22.Generate Parentheses[M]括号生成

题目

Given n pairs of parentheses, write a function to generate all combinations of well-formed parentheses.

For example, given n=3, a solution set is:

 [

  "( ( ( ) ) )",

  "( ( ) ( ) )",

  "( ( ) ) ( )",

  "( ) ( ( ) )",

  "( ) ( ) ( )"

 ]

---

思路

回溯法

对于\(n\)对有效括号的生成，我们可以将其看成以下的方式：

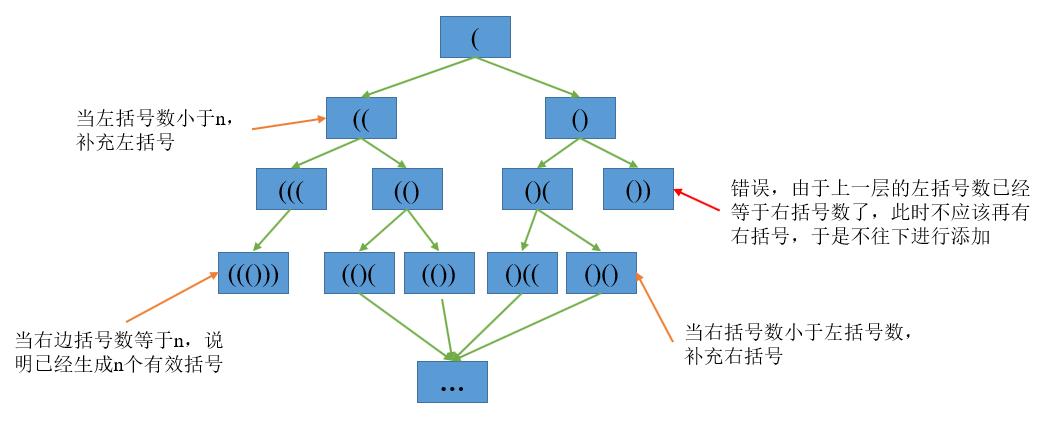
图1：回溯法生成括号示意图
在上图中，由于一对有效括号总是从"("开始，所以树的根节点是"("。将左括号的个数记为$l$，右括号的个数记为$r$，给定个数$n$，在生成新括号的过程中，分为三种情况
* $l r$，说明右括号的个数不够多，应该生成右括号
* $r = n$，说明完成$n$对有效括号的生成。

注意在此过程中，右括号的个数不能超过左括号，如果超过，则不往下进行递归。由此完成了一个回溯法的过程：递归生成括号，但是在生成括号的同时，检查左右括号是否匹配。如果匹配，则继续递归；如果不匹配，则不往下递归。在具体实现中，通过保证右边括号的个数\(r\)始终小于等于左边括号的个数来实现匹配的检查。

---

Tips

回溯法

基本思想

将问题的解空间转化为图或者树的结构表示，然后利用深度优先搜索策略进行遍历，遍历过程中记录和寻找可行解和最优解。

基本行为

回溯法的基本行为是搜索，在搜索过程中利用两种方法来避免无效的搜索

• 1.使用约束函数，剪去不满足约束条件的路径
• 2.使用限定条件，剪去不能得到最优解的路径
  
  回溯法是一种思想方法，在具体实现中是通过递归或者迭代实现。

---

C++

 vector<string> generateParenthesis(int n) {

        vector<string> result;  

        if(n==0)
            return result;

        backTrack(result, "", 0, 0, n);

        return result;
    }

    void backTrack(vector<string> &res,string curStr,int l, int r, int n){

        if(r == n)
            res.push_back(curStr);

        //如果左括号没有达到给定的n
        if(l < n)
            backTrack(res, curStr+"(", l+1, r, n);

        //如果右括号数目不够
        if(r < l)
            backTrack(res, curStr+")", l, r+1, n);
    }

---

Python

参考

[1]

[2] https://blog.csdn.net/zjc_game_coder/article/details/78520742