2018年江西理工大学C语言程序设计竞赛高级组部分题解

B Interesting paths

　　考察范围：组合数学

　　此题是机器人走方格的变种，n*m的网格，从(1,1)走到(n,m)，首先可以明确，水平要走m-1格，竖直要走n-1格，则走到目的地的任意一条路径必须走n+m-2格，呢么只要确定竖直要走的，剩下的就是水平要走的，则答案为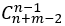

。

　　在Interseting paths要求左下角和右上角两个小矩阵不能走，则需要把整个网格依据两个小矩阵的水平和竖直边界分为两部分，依次运用组合数。例如

灰色区域之外为可走区域，分为两部分棕色，和黄色，则结果为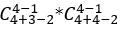

若是这种情况，则可分为两个

   

则结果为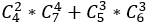

所以需要两次分割，分别处理c到a和b到d。

因为n，m的范围比较大，可以提前预处理1到2*10^5的所有组合数和逆元。

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <vector>
#include <queue>
#include <stack>
#include <cstdlib>
#include <iomanip>
#include <cmath>
#include <cassert>
#include <ctime>
#include <map>
#include <set>
using namespace std;
#pragma comment(linker, "/stck:1024000000,1024000000")
#pragma GCC diagnostic error "-std=c++11"
#define lowbit(x) (x&(-x))
#define max(x,y) (x>=y?x:y)
#define min(x,y) (x<=y?x:y)
#define MAX 100000000000000000
#define MOD 998244353
#define pi acos(-1.0)
#define ei exp(1)
#define PI 3.1415926535897932384626433832
#define ios() ios::sync_with_stdio(true)
#define INF 0x3f3f3f3f
#define mem(a) ((a,0,sizeof(a)))
typedef long long ll;
;
ll fic[],jie[];
ll t,n,m,a,b,c,d;
ll quick_pow(ll x,ll y){//求逆元
    ll ans=;
    while(y){
        ) ans=ans*x%mod;
        y>>=;
        x=x*x%mod;
    }
    return ans;
}
void get_fic(){
    fic[]=;
    jie[]=quick_pow(fic[],mod-);
    ;i<=;i++){
        fic[i]=fic[i-]*i%mod;
        jie[i]=quick_pow(fic[i],mod-);
    }
}
int main(){
    get_fic();//预处理所有值
    scanf("%lld",&t);
    while(t--){
        scanf("%lld%lld%lld%lld%lld%lld",&n,&m,&a,&b,&c,&d);
        ll ans=;
        ;i<a;i++){//竖直处理
            ll l=fic[b+i-]*jie[b-]%mod*jie[i-]%mod;
            ll r=fic[m-b+n-i-]*jie[m-b-]%mod*jie[n-i]%mod;
            ans=(ans+(l*r)%mod)%mod;
        }
        ;i<d;i++){//水平处理
            ll l=fic[c+i-]*jie[c-]%mod*jie[i-]%mod;
            ll r=fic[m-i+n-c-]*jie[m-i]%mod*jie[n-c-]%mod;
            ans=(ans+(l*r)%mod)%mod;
        }
        printf("%lld\n",ans);
    }
    ;
}

C 三角平方数

　　设三角数为m，平方数为n则根据题意有n^2=(1/2)(m+1)m,化简可得 8n^2=4m^2+4m+1-1==>

(2m+1)^2-2(2n)^2=1

令x=2m+1,y=2n则有 x^2-2y^2=1可知为佩尔方程标准形式，特解为x=3,y=2,所以可以转化为矩阵乘法求任意一个解（佩尔方程）。

import java.util.*;
import java.io.*;
import java.math.*;
public class Main{
    static Scanner cin=new Scanner(System.in);
    static PrintWriter cout=new PrintWriter(System.out,true);
    public static BigInteger[][] multiply_matrix(BigInteger[][] a,BigInteger[][] b){
        BigInteger[][] c=new BigInteger[2][2];
        c[0][0]=BigInteger.valueOf(0);
        c[0][1]=BigInteger.valueOf(0);
        c[1][0]=BigInteger.valueOf(0);
        c[1][1]=BigInteger.valueOf(0);
        for(int i=0;i<2;i++)
            for(int j=0;j<2;j++)
                for(int k=0;k<2;k++)
                    c[i][j]=c[i][j].add(a[i][k].multiply(b[k][j]));
        return c;
    }
    public static BigInteger quick_pow(int y){
    BigInteger[][] ans=new BigInteger[2][2];
    BigInteger[][] pos=new BigInteger[2][2];
        ans[0][0]=BigInteger.valueOf(1);
        ans[0][1]=BigInteger.valueOf(0);
        ans[1][0]=BigInteger.valueOf(0);
        ans[1][1]=BigInteger.valueOf(1);
        pos[0][0]=BigInteger.valueOf(3);
        pos[0][1]=BigInteger.valueOf(4);
        pos[1][0]=BigInteger.valueOf(2);
        pos[1][1]=BigInteger.valueOf(3);
        while(y!=0){
            if(y%2==1) ans=multiply_matrix(ans,pos);
            y=y/2;
            pos=multiply_matrix(pos,pos);
        }
        return ans[1][0];
    }
    public static void main(String[] args){
        int n=cin.nextInt();
        BigInteger result=quick_pow(n);
        result=result.divide(BigInteger.valueOf(2));
        cout.println(result.multiply(result));
    }
}

F Star

　　考察范围：最小生成树

　　任意两个主星球之间都可以选择是否进行空间奇点压缩，选择不压缩就是三维排序，压缩就分别去掉x,y,z进行二维排序，最后跑最小生成树即可。

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <vector>
#include <queue>
#include <stack>
#include <cstdlib>
#include <iomanip>
#include <cmath>
#include <cassert>
#include <ctime>
#include <map>
#include <set>
using namespace std;
#pragma comment(linker, "/stck:1024000000,1024000000")
#pragma GCC diagnostic error "-std=c++11"
#define lowbit(x) (x&(-x))
#define max(x,y) (x>=y?x:y)
#define min(x,y) (x<=y?x:y)
#define MAX 100000000000000000
#define MOD 1000000007
#define pi acos(-1.0)
#define ei exp(1)
#define PI 3.1415926535897932384626433832
#define ios() ios::sync_with_stdio(true)
#define INF 0x3f3f3f3f
#define mem(a) (memset(a,0,sizeof(a)))
typedef long long ll;
];
ll n,k;
struct f{
  ll x,y,z;
  int id;
}edge[];
struct node{
  int u,v;
  ll dis;
  bool operator<(const node &a) const{
    return a.dis>dis;
  }
}e[];
int find(int x){
  return fa[x]=(fa[x]==x?x:find(fa[x]));
}
bool cmp_xyz(f a,f b){//自定义排序
  return a.x+a.y+a.z<b.x+b.y+b.z;
}
bool cmp_xy(f a,f b){
  return a.x+a.y<b.x+b.y;
}
bool cmp_xz(f a,f b){
  return a.x+a.z<b.x+b.z;
}
bool cmp_yz(f a,f b){
  return a.z+a.y<b.z+b.y;
}
int main(){
  scanf("%lld%lld",&n,&k);
  ;i<n;i++){
    scanf("%lld%lld%lld",&edge[i].x,&edge[i].y,&edge[i].z);
    edge[i].id=i+;
  }
  ;i<=n;i++)
    fa[i]=i;
  ;
  sort(edge,edge+n,cmp_xyz);
  ;i<n;i++)
    e[ans++]=(node){edge[i].id,edge[i-].id,edge[i].x+edge[i].y+edge[i].z-edge[i-].x-edge[i-].y-edge[i-].z};
  sort(edge,edge+n,cmp_xy);
  ;i<n;i++)
    e[ans++]=(node){edge[i].id,edge[i-].id,edge[i].x+edge[i].y-edge[i-].x-edge[i-].y};
  sort(edge,edge+n,cmp_xz);
  ;i<n;i++)
    e[ans++]=(node){edge[i].id,edge[i-].id,edge[i].x+edge[i].z-edge[i-].x-edge[i-].z};
  sort(edge,edge+n,cmp_yz);
  ;i<n;i++)
    e[ans++]=(node){edge[i].id,edge[i-].id,edge[i].z+edge[i].y-edge[i-].z-edge[i-].y};
  ;
  sort(e,e+ans);
  ll inf=;
  ;i<ans && pos>;i++){//最小生成树kruskal写法
    int x=find(e[i].u);
    int y=find(e[i].v);
    if(x!=y){
      inf+=e[i].dis;
      fa[x]=y;
      pos--;
    }
  }
  printf("%lld\n",inf*k);
  ;
}