Codeforces Round #373 (Div. 2) E. Sasha and Array 矩阵快速幂+线段树

E. Sasha and Array

time limit per test

5 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Sasha has an array of integers a1, a2, ..., an. You have to perform m queries. There might be queries of two types:

1. 1 l r x — increase all integers on the segment from l to r by values x;
2. 2 l r — find 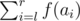, where f(x) is the x-th Fibonacci number. As this number may be large, you only have to find it modulo109 + 7.

In this problem we define Fibonacci numbers as follows: f(1) = 1, f(2) = 1, f(x) = f(x - 1) + f(x - 2) for all x > 2.

Sasha is a very talented boy and he managed to perform all queries in five seconds. Will you be able to write the program that performs as well as Sasha?

Input

The first line of the input contains two integers n and m (1 ≤ n ≤ 100 000, 1 ≤ m ≤ 100 000) — the number of elements in the array and the number of queries respectively.

The next line contains n integers a1, a2, ..., an (1 ≤ ai ≤ 109).

Then follow m lines with queries descriptions. Each of them contains integers tpi, li, ri and may be xi (1 ≤ tpi ≤ 2, 1 ≤ li ≤ ri ≤ n,1 ≤ xi ≤ 109). Here tpi = 1 corresponds to the queries of the first type and tpi corresponds to the queries of the second type.

It's guaranteed that the input will contains at least one query of the second type.

Output

For each query of the second type print the answer modulo 109 + 7.

Examples

input

5 4
1 1 2 1 1
2 1 5
1 2 4 2
2 2 4
2 1 5

output

5
7
9

Note

Initially, array a is equal to 1, 1, 2, 1, 1.

The answer for the first query of the second type is f(1) + f(1) + f(2) + f(1) + f(1) = 1 + 1 + 1 + 1 + 1 = 5.

After the query 1 2 4 2 array a is equal to 1, 3, 4, 3, 1.

The answer for the second query of the second type is f(3) + f(4) + f(3) = 2 + 3 + 2 = 7.

The answer for the third query of the second type is f(1) + f(3) + f(4) + f(3) + f(1) = 1 + 2 + 3 + 2 + 1 = 9.

题意：f（x）为斐波那契第x项，1是更新l-r的区间f（i+x），2是求区间和；

思路：线段树维护矩阵，将每个f(x)转化为2*2的矩阵，区间更新为乘法；

　　  需要一点小优化；

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define pi (4*atan(1.0))
const int N=1e5+,M=4e6+,inf=1e9+,mod=1e9+;
struct is
{
    ll a[][];
    void setnum(ll aa,ll b,ll c,ll d)
    {
        a[][]=aa;
        a[][]=b;
        a[][]=c;
        a[][]=d;
    }
    void reset()
    {
        for(int i=;i<=;i++)
            for(int t=;t<=;t++)
            a[i][t]=;
    }
};
is add(is a,is b)
{
    for(int i=; i<=; i++)
        for(int t=; t<=; t++)
            a.a[i][t]=(a.a[i][t]+b.a[i][t])%mod;
    return a;
}
struct tree
{
    is lazy;
    is a;
}tree[N<<];
is gg;
is juzhenmul(is a,is b,ll mod)
{
    int i,t,j;
    is ans;
    ans.reset();
    for(i=;i<=;i++)
    for(t=;t<=;t++)
    for(j=;j<=;j++)
    {
        ans.a[i][t]+=(a.a[i][j]*b.a[j][t]);
        ans.a[i][t]%=mod;
    }
    return ans;
}
is quickpow(is a,ll x,ll mod)
{
    is ans;
    ans.setnum(,,,);
    while(x)
    {
        if(x&)  ans=juzhenmul(ans,a,mod);
        a=juzhenmul(a,a,mod);
        x>>=;
    }
    return ans;
}
is getans(is base,ll x,ll mod)
{
    return quickpow(base,x-,mod);
}
void pushup(int pos)
{
    tree[pos].a=add(tree[pos<<|].a,tree[pos<<].a);
}
void pushdown(int pos)
{
    if(tree[pos].lazy.a[][]!=||tree[pos].lazy.a[][]!=||tree[pos].lazy.a[][]!=||tree[pos].lazy.a[][]!=)
    {
        tree[pos<<].lazy=juzhenmul(tree[pos<<].lazy,tree[pos].lazy,mod);
        tree[pos<<|].lazy=juzhenmul(tree[pos<<|].lazy,tree[pos].lazy,mod);
        tree[pos<<].a=juzhenmul(tree[pos].lazy,tree[pos<<].a,mod);
        tree[pos<<|].a=juzhenmul(tree[pos].lazy,tree[pos<<|].a,mod);
        tree[pos].lazy.setnum(,,,);
    }
}
void buildtree(int l,int r,int pos)
{
    tree[pos].lazy.setnum(,,,);
    if(l==r)
    {
        ll x;
        scanf("%lld",&x);
        tree[pos].a=getans(gg,x,mod);
        return;
    }
    int mid=(l+r)>>;
    buildtree(l,mid,pos<<);
    buildtree(mid+,r,pos<<|);
    pushup(pos);
}
void update(int L,int R,int l,int r,int pos,is c)
{
    if(L<=l&&r<=R)
    {
        tree[pos].lazy=juzhenmul(c,tree[pos].lazy,mod);
        tree[pos].a=juzhenmul(c,tree[pos].a,mod);
        return;
    }
    pushdown(pos);
    int mid=(l+r)>>;
    if(L<=mid)
    update(L,R,l,mid,pos<<,c);
    if(R>mid)
    update(L,R,mid+,r,pos<<|,c);
    pushup(pos);
}
ll query(int L,int R,int l,int r,int pos)
{
    if(L<=l&&r<=R)
    return tree[pos].a.a[][];
    pushdown(pos);
    int mid=(l+r)>>;
    ll ans=;
    if(L<=mid)
    ans+=query(L,R,l,mid,pos<<);
    if(R>mid)
    ans+=query(L,R,mid+,r,pos<<|);
    return ans%mod;
}
int main()
{
    gg.setnum(,,,);
    int n,m;
    scanf("%d%d",&n,&m);
    buildtree(,n,);
    while(m--)
    {
        int flag,l,r;
        ll c;
        scanf("%d%d%d",&flag,&l,&r);
        if(flag==)
        {
            scanf("%lld",&c);
            update(l,r,,n,,getans(gg,c+,mod));
        }
        else
        printf("%lld\n",query(l,r,,n,));
    }
    return ;
}