洛谷 P2168 [NOI2015]荷马史诗 解题报告

P2168 [NOI2015]荷马史诗

题目描述

追逐影子的人，自己就是影子 ——荷马

Allison 最近迷上了文学。她喜欢在一个慵懒的午后，细细地品上一杯卡布奇诺，静静地阅读她爱不释手的《荷马史诗》。但是由《奥德赛》和《伊利亚特》 组成的鸿篇巨制《荷马史诗》实在是太长了，Allison 想通过一种编码方式使得它变得短一些。

一部《荷马史诗》中有\(n\)种不同的单词，从\(1\)到\(n\)进行编号。其中第i种单 词出现的总次数为\(w_i\)。Allison 想要用\(k\)进制串\(s_i\)来替换第i种单词，使得其满足如下要求：

对于任意的 \(1\le i, j \le n\) ， \(i ≠ j\) ，都有：\(s_i\)不是\(s_j\)的前缀。

现在 Allison 想要知道，如何选择\(s_i\)，才能使替换以后得到的新的《荷马史诗》长度最小。在确保总长度最小的情况下，Allison 还想知道最长的si的最短长度是多少？

一个字符串被称为k进制字符串，当且仅当它的每个字符是 \(0\) 到 \(k − 1\) 之间（包括 \(0\) 和 \(k − 1\) ）的整数。

字符串 \(str1\) 被称为字符串 \(str2\) 的前缀，当且仅当：存在 \(1 ≤ t ≤ m\) ，使得\(str1 = str2[1..t]\)。其中，\(m\)是字符串\(str2\)的长度，\(str2[1..t]\) 表示\(str2\)的前\(t\)个字符组成的字符串。

输入输出格式

输入格式：

输入的第 1 行包含 2 个正整数 \(n\), \(k\) ，中间用单个空格隔开，表示共有 \(n\)种单词，需要使用\(k\)进制字符串进行替换。

接下来\(n\)行，第 \(i + 1\) 行包含 1 个非负整数\(w_i\) ，表示第 \(i\) 种单词的出现次数。

输出格式：

输出包括 2 行。

第 1 行输出 1 个整数，为《荷马史诗》经过重新编码以后的最短长度。

第 2 行输出 1 个整数，为保证最短总长度的情况下，最长字符串 si 的最短长度。

说明：

---

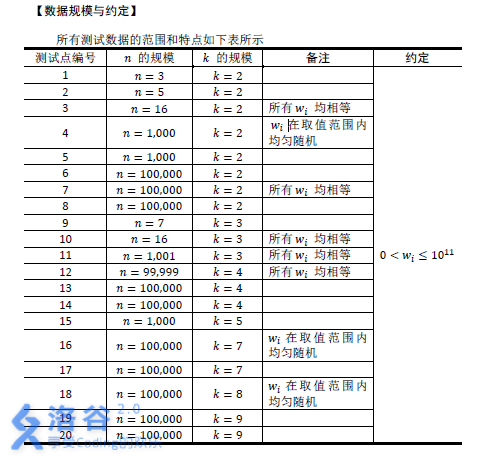
如果把编码集合建成字典树，满足所有的编码不是别的的前缀即为所有的编码都在叶子节点结束

总代价为\(\sum w_i*len_i\)，\(len_i\)为长度

其实就是在求\(k\)叉哈弗曼树

我们将节点补全至满足\((k-1)|(n-1)\)，保证上面的叶子都填满了

然后从小的值开始放叶子节点

---

Code:

#include <cstdio>
#include <queue>
#define ll long long
using namespace std;
struct node
{
    ll w,d;
    bool friend operator <(node n1,node n2)
    {
        return n1.w==n2.w?n1.d>n2.d:n1.w>n2.w;
    }
}t;
priority_queue <node> q;
int n,k;
int main()
{
    scanf("%d%d",&n,&k);
    t.d=0;
    for(int i=1;i<=n;i++)
    {
        scanf("%lld",&t.w);
        q.push(t);
    }
    t.w=0;ll ans=0,mx=0;
    while((n-1)%(k-1)!=0) q.push(t),++n;
    while(q.size()>1)
    {
        t.d=t.w=0;
        for(int i=1;i<=k;i++)
        {
            t.w+=q.top().w,t.d=max(q.top().d,t.d);
            q.pop();
        }
        ++t.d,ans+=t.w,mx=max(mx,t.d);
        q.push(t);
    }
    printf("%lld\n%lld\n",ans,mx);
    return 0;
}

---

2018.8.31