P4578 [FJOI2018]所罗门王的宝藏

传送门

考虑一个位置答案传递性，如果某个位置的红宝石转动确定了，那么会引起连锁反应：

如图，绿色的转动确定了，那么那两个蓝色的转动也确定了

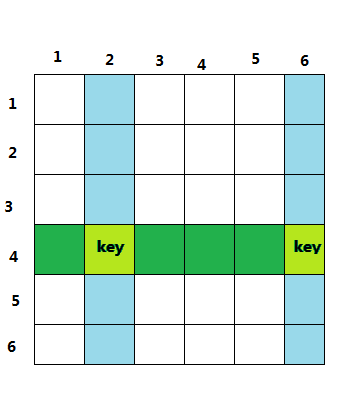
自己手玩一下，发现如果有解那么随便找一个开始然后一路玩下去最后一定会有解，如果一旦有冲突那么之后不管怎么调整也都一定无解，（因为调整最后又会绕回自己继续冲突）

然后就直接BFS搜就好了

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<cstring>
#include<queue>
using namespace std;
inline int read()
{
    int x=,f=; char ch=getchar();
    while(ch<''||ch>'') { if(ch=='-') f=-; ch=getchar(); }
    while(ch>=''&&ch<='') { x=(x<<)+(x<<)+(ch^); ch=getchar(); }
    return x*f;
}
const int N=;
int fir[N],from[N],to[N],val[N],cntt;
inline void add(int a,int b,int c)
{
    from[++cntt]=fir[a];
    fir[a]=cntt; to[cntt]=b; val[cntt]=c;
}
int T,n,m,K;
int del[N];
bool vis[N],GG;
void BFS(int st)
{
    queue <int> q;
    q.push(st); vis[st]=;
    while(!q.empty())
    {
        int x=q.front(); q.pop();
        for(int i=fir[x];i;i=from[i])
        {
            int &v=to[i],&w=val[i];
            if(vis[v])
            {
                if(del[v]!=w-del[x]) { GG=; return; }
                continue;
            }
            del[v]=w-del[x]; vis[v]=;
            q.push(v);
        }
    }
}
int main()
{
    int a,b,c;
    T=read();
    while(T--)
    {
        memset(vis,,sizeof(vis)); memset(del,,sizeof(del));
        memset(fir,,sizeof(fir)); cntt=; GG=;
        n=read(); m=read(); K=read();
        for(int i=;i<=K;i++)
        {
            a=read(); b=read(); c=read();
            add(a,b+n,c); add(b+n,a,c);
        }
        for(int i=;i<=n+m;i++)
        {
            if(!vis[i]) BFS(i);
            if(GG) break;
        }
        if(GG) printf("No\n");
        else printf("Yes\n");
    }
    return ;
}