Deep Learning（Ian Goodfellow） — Chapter2 Linear Algebra

　　线性代数是机器学习的数学基础之一，这里总结一下深度学习花书线性代数一章中机器学习主要用到的知识，并不囊括所有线性代数知识。

2.1 基础概念

• Scalars: 一个数；
• Vctors: 一列数；
• Matrices: 二位数组的数，每个元素由两个下标确定；
• Tensors: 多维数组的数。

2.2  矩阵计算

转置（transpose）：(AT)i,j=Aj,i

矩阵乘法: C=AB，

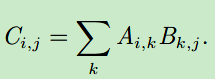
元素乘法(element product; Hardamard product)：A⨀B

点乘(dot product): 向量x，y的点乘： xTy

单位矩阵(identic matrix): In， 斜对角的元素值是1,其他地方都是0

逆矩阵（inverse matrix）:

    

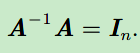
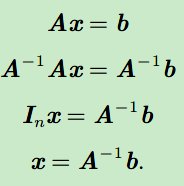
2.3  线性相关和生成子空间

线性组合（linear combination）：

• 将矩阵A看作是不同的列向量的组合[d1,d2,...,dn]，每个列向量代表一个方向，x可以代表在每个方向上移动的距离，那么Ax=b可以理解成原点如何在AA指定的各个方向上移动，最后到达b点。
• Ax即为线性组合，组合的对象是各个列向量，方式是x的元素。

生成空间（span）：对所有的x，生成的点Ax的集合，即为A的生成空间。如果一组向量中的任意一个向量都不能表示成其他向量的线性组合，那么这组向量称为线性无关（linearly independent）。如果某个向量是一组向量中某些向量的线性组合，那么我们将这个向量加入这组向量后不会增加这组向量的生成子空间。这意味着，如果一个矩阵的列空间涵盖整个Rm ，那么该矩阵必须包含至少一组m 个线性无关的向量。

2.4  范数

范数（Norm）：

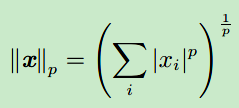
2.5  矩阵和向量

对角阵（diagnal matrix）：除了对角线上的元素不为0,其他元素都为0。可以表示为diag(v)。

对称阵（symmetric matrix）：A=AT

单位向量（unit vector）：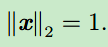

正交（orthogonal）：

2.6  特征分解

特征分解：

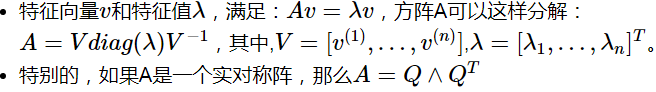
　　我们可以想象矩阵A实际上是将空间在其本征向量的方向上各自拉伸了对应的本征值的尺度。

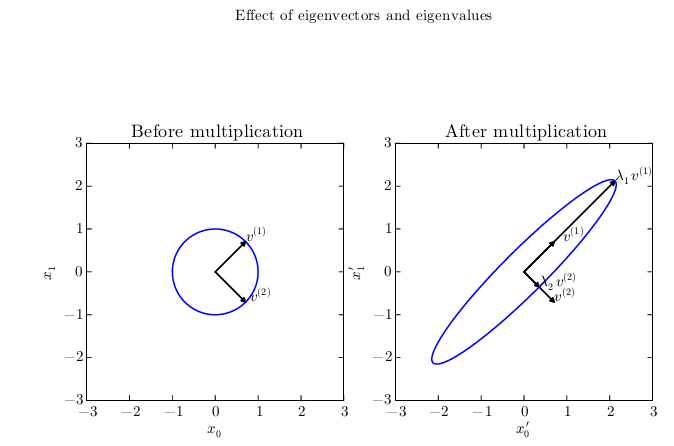
2.7  奇异值分解（singular value decomposition）：

　　SVD全称是Single Value Decomposition奇异值分解。和特征分解类似，它也是将矩阵分解为更基本的组合乘积，而且SVD更具有普适性，对于矩阵本身的要求很少，基本上所有实数矩阵都可以做SVD分解，而特征分解对于非对称矩阵是无能为力的。

　　

　　这些矩阵中的每一个经定义后都拥有特殊的结构。矩阵U 和V 都定义为正交矩阵，而矩阵D 定义为对角矩阵。注意，矩阵D 不一定是方阵。对角矩阵D 对角线上的元素被称为矩阵A 的奇异值（singular value）。矩阵U 的列向量被称为左奇异向量（left singular vector），矩阵V 的列向量被称右奇异向量（right singular vector）。事实上，我们可以用与A 相关的特征分解去解释A 的奇异值分解。A 的左奇异向量（left singular vector）是AA⊤ 的特征向量。A 的右奇异向量（right singular vector）是A⊤ A 的特征向量。A 的非零奇异值是A⊤ A 特征值的平方根，同时也是AA⊤ 特征值的平方根。

2.8   迹运算

行列式（Determinant）：

• det(A)，是一个将一个matrix映射到一个实数的function。
• 行列式的值等于矩阵的所有特征值的乘积。
• 行列式，记作det(A)，是一个将方阵A 映射到实数的函数。行列式等于矩阵特征值的乘积。行列式的绝对值可以用来衡量矩阵参与矩阵乘法后空间扩大或者缩小了多少。如果行列式是0，那么空间至少沿着某一维完全收缩了，使其失去了所有的体积。如果行列式是1，那么这个转换保持空间体积不变。

　　本章还有一个主成分析(PCA)的例子，准备之后讲经典机器学习无监督算法的时候再一并总结，放到第五章比较合适。

参考文献：

https://zhuanlan.zhihu.com/p/38431213

http://www.deeplearningbook.org/

https://applenob.github.io/deep_learning_1.html