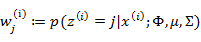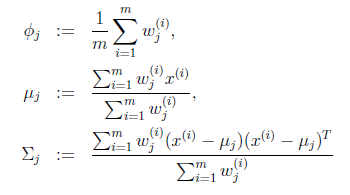高斯混合模型和EM算法
使用期望最大化算法(Expectation-Maximization)来进行密度估计(density estimation)。
与k-means一样,给定的训练样本是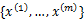 ,我们将隐含类别标签用
,我们将隐含类别标签用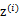 表示。与k-means的硬指定不同,我们首先认为
表示。与k-means的硬指定不同,我们首先认为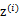 是满足一定的概率分布的,这里我们认为满足多项式分布,
是满足一定的概率分布的,这里我们认为满足多项式分布,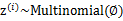 ,其中
,其中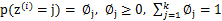 ,
,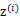 有k个值{1,…,k}可以选取。而且我们认为在给定
有k个值{1,…,k}可以选取。而且我们认为在给定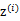 后,
后,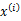 满足多值高斯分布,即
满足多值高斯分布,即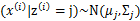 。由此可以得到联合分布
。由此可以得到联合分布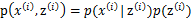 。
。
整个模型简单描述为对于每个样例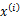 ,我们先从k个类别中按多项式分布抽取一个
,我们先从k个类别中按多项式分布抽取一个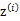 ,然后根据
,然后根据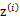 所对应的k个多值高斯分布中的一个生成样例
所对应的k个多值高斯分布中的一个生成样例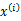 ,。整个过程称作混合高斯模型。注意的是这里的
,。整个过程称作混合高斯模型。注意的是这里的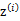 仍然是隐含随机变量。模型中还有三个变量
仍然是隐含随机变量。模型中还有三个变量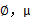 和
和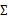 。最大似然估计为
。最大似然估计为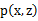 。对数化后如下:
。对数化后如下:
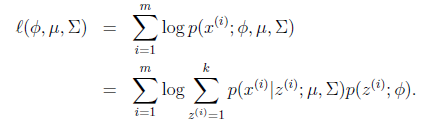
这个式子的最大值是不能通过前面使用的求导数为0的方法解决的,因为求的结果不是close form。但是假设我们知道了每个样例的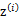 ,那么上式可以简化为:
,那么上式可以简化为:
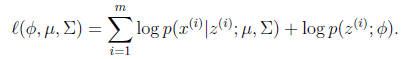
这时候我们再来对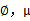 和
和 进行求导得到:
进行求导得到:
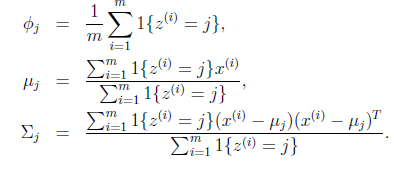
 就是样本类别中
就是样本类别中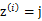 的比率。
的比率。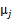 是类别为j的样本特征均值,
是类别为j的样本特征均值,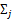 是类别为j的样例的特征的协方差矩阵。
是类别为j的样例的特征的协方差矩阵。
实际上,当知道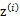 后,最大似然估计就近似于高斯判别分析模型(Gaussian
后,最大似然估计就近似于高斯判别分析模型(Gaussian
discriminant analysis model)了。所不同的是GDA中类别y是伯努利分布,而这里的z是多项式分布,还有这里的每个样例都有不同的协方差矩阵,而GDA中认为只有一个。
之前我们是假设给定了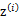 ,实际上
,实际上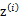 是不知道的。那么怎么办呢?考虑之前提到的EM的思想,第一步是猜测隐含类别变量z,第二步是更新其他参数,以获得最大的最大似然估计。用到这里就是:
是不知道的。那么怎么办呢?考虑之前提到的EM的思想,第一步是猜测隐含类别变量z,第二步是更新其他参数,以获得最大的最大似然估计。用到这里就是:
|
循环下面步骤,直到收敛: { (E步)对于每一个i和j,计算
(M步),更新参数:
} |
在E步中,我们将其他参数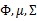 看作常量,计算
看作常量,计算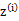 的后验概率,也就是估计隐含类别变量。估计好后,利用上面的公式重新计算其他参数,计算好后发现最大化最大似然估计时,
的后验概率,也就是估计隐含类别变量。估计好后,利用上面的公式重新计算其他参数,计算好后发现最大化最大似然估计时,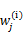 值又不对了,需要重新计算,周而复始,直至收敛。
值又不对了,需要重新计算,周而复始,直至收敛。
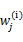 的具体计算公式如下:
的具体计算公式如下:
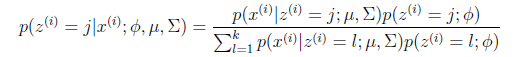
这个式子利用了贝叶斯公式。
这里我们使用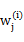 代替了前面的
代替了前面的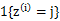 ,由简单的0/1值变成了概率值。
,由简单的0/1值变成了概率值。
对比K-means可以发现,这里使用了“软”指定,为每个样例分配的类别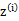 是有一定的概率的,同时计算量也变大了,每个样例i都要计算属于每一个类别j的概率。与K-means相同的是,结果仍然是局部最优解。对其他参数取不同的初始值进行多次计算不失为一种好方法。
是有一定的概率的,同时计算量也变大了,每个样例i都要计算属于每一个类别j的概率。与K-means相同的是,结果仍然是局部最优解。对其他参数取不同的初始值进行多次计算不失为一种好方法。
虽然之前再K-means中定性描述了EM的收敛性,仍然没有定量地给出,还有一般化EM的推导过程仍然没有给出。下一篇着重介绍这些内容。
高斯混合模型和EM算法的更多相关文章
- 最大熵模型和EM算法
一.极大似然已经发生的事件是独立重复事件,符合同一分布已经发生的时间是可能性(似然)的事件利用这两个假设,已经发生时间的联合密度值就最大,所以就可以求出总体分布f中参数θ 用极大似然进行机器学习有监督 ...
- 混合高斯模型和EM算法
这篇讨论使用期望最大化算法(Expectation-Maximization)来进行密度估计(density estimation). 与k-means一样,给定的训练样本是,我们将隐含类别标签用表示 ...
- 高斯混合模型参数估计的EM算法
# coding:utf-8 import numpy as np def qq(y,alpha,mu,sigma,K,gama):#计算Q函数 gsum=[] n=len(y) for k in r ...
- 高斯混合聚类及EM实现
一.引言 我们谈到了用 k-means 进行聚类的方法,这次我们来说一下另一个很流行的算法:Gaussian Mixture Model (GMM).事实上,GMM 和 k-means 很像,不过 G ...
- 高斯混合模型GMM与EM算法的Python实现
GMM与EM算法的Python实现 高斯混合模型(GMM)是一种常用的聚类模型,通常我们利用最大期望算法(EM)对高斯混合模型中的参数进行估计. 1. 高斯混合模型(Gaussian Mixture ...
- 混合高斯分布与 EM 算法
极大似然估计在混合高斯分布中遇到的困难 在一般的情况下,对于所得到的样本集,\(X=\left\{x_{1}, \dots, x_{N}\right\}\),我们的目标是最大化似然函数,通过最大化似然 ...
- 混合高斯模型和EM
<统计学习方法>这本书上写的太抽象,可参考这位大神的:http://www.cnblogs.com/jerrylead/archive/2011/04/06/2006924.html
- HMM模型和Viterbi算法
https://www.cnblogs.com/Denise-hzf/p/6612212.html 一.隐含马尔可夫模型(Hidden Markov Model) 1.简介 隐含马尔可夫模型并不是俄罗 ...
- 机器学习算法总结(六)——EM算法与高斯混合模型
极大似然估计是利用已知的样本结果,去反推最有可能(最大概率)导致这样结果的参数值,也就是在给定的观测变量下去估计参数值.然而现实中可能存在这样的问题,除了观测变量之外,还存在着未知的隐变量,因为变量未 ...
随机推荐
- PHP + JavaScript + Ajax 实现无刷新页面加载效果
数据源工厂 Json生成方式1 Json生成方式2 数据搬运工 数据加工师 转换类型 加工展示 结果展示 初始页面 点击按钮之后 总结 今天这个实验的思路就是实现一个无刷新的页面加载效果.具体的思路是 ...
- setting.py
""" Django settings for sitea project. For more information on this file, see https:/ ...
- 基于V4L2摄像头采集图片程序设计
#ifndef __COMMON_H #define __COMMON_H //该头文件定义的是摄像头在屏幕上显示的宽度和高度 #include<stdio.h> #include< ...
- 剑指Offer--排序算法小结
剑指Offer--排序算法小结 前言 毕业季转眼即到,工作成为毕业季的头等大事,必须得认认真真进行知识储备,迎战笔试.电面.面试. 许久未接触排序算法了.平时偶尔接触到时自己会不假思索的百度,然后就是 ...
- 对Bitmap的内存优化
在Android应用里,最耗费内存的就是图片资源.而且在Android系统中,读取位图Bitmap时,分给虚拟机中的图片的堆栈大小只有8M,如果超出了,就会出现OutOfMemory异常.所以,对于图 ...
- FFmpeg示例程序合集-批量编译脚本
此前做了一系列有关FFmpeg的示例程序,组成了<最简单的FFmpeg示例程序合集>,其中包含了如下项目:simplest ffmpeg player: ...
- Ruby开发入门
开发环境搭建 首先安装Ruby SDK,我安装的版本是2.0.之后安装IDE,这里用的是Jetbrain的RubyMine 5.4.3,注意是否支持对应版本的Ruby SDK. 一段神奇的注册码... ...
- Android开发工具下载地址
Android Studio: http://zdz.la/iq4zSa
- iOS中 加强日志输出 开发技术总结
对于那些做后端开发的工程师来说,看LOG解Bug应该是理所当然的事,但我接触到的移动应用开发的工程师里面,很多人并没有这个意识,查Bug时总是一遍一遍的试图重现,试图调试,特别是对一些不太容易重现的B ...
- Spring注入
Spring注入 Spring注入是指在启动Spring容器加载bean配置的时候,完成对变量的赋值行为. 常用的两种注入方式: setter注入 构造注入 <?xml version=&quo ...