loj2880「JOISC 2014 Day3」稻草人

题目链接：bzoj4237

​ loj2880

考虑\(cdq\)分治，按\(x\)坐标排序，于是问题变成统计左下角在\([l,mid]\)，右上角在\([mid+1,r]\)的矩形数量

我们先考虑固定左下角，来看一下右上角是如何变化的

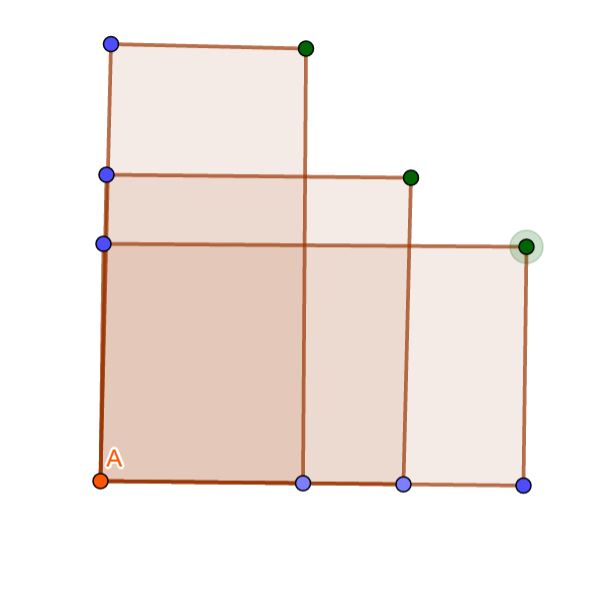
当我们固定左下角A（橙色点）的时候，我们注意到右上角的点的\(x\)坐标单调递减，\(y\)单调递增

我们再考虑左下角发生变化的情况

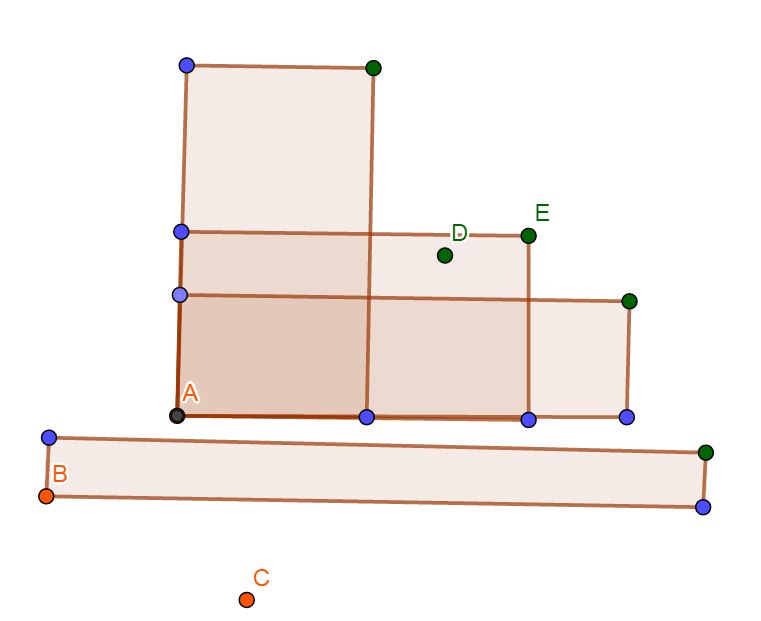
此时左边有三个点\(A,B,C\)，右边有四个绿色的点（不含点\(D\)），\(A\)可以和右边上方的三个点产生贡献，\(B\)只能和右边最下方的一个点产生贡献，\(C\)可以和右边的所有点产生贡献。说明对于左边的两个点\(P\)和\(Q\)，如果满足\(P_x<Q_x\)且\(P_y>Q_y\)，那么可以与\(P\)产生贡献的点也可以与\(Q\)产生贡献

再来看一下上图，假设多了一个点\(D\)，注意到点\(D\)在点\(E\)的左下方，这使得点\(E\)一定不会产生贡献

同理，对于左边的点，只有当前的点的左上方有原来的点的情况下，这个点和右边的点的组合才会产生影响

于是解法就比较清晰了

对于左边的点和右边的点分别维护一个单调栈，左边的点的\(x\)单调递减，右边的点的\(x\)单调递增，每次将\(y\)从小到大进行排序依次加点，维护单调栈的同时二分\(y\)统计右边有多少个合法点

#include<iostream>
#include<string.h>
#include<string>
#include<stdio.h>
#include<algorithm>
#include<math.h>
#include<vector>
#include<queue>
#include<map>
#include<set>
using namespace std;
#define lowbit(x) (x)&(-x)
#define fir first
#define sec second
#define rep(i,a,b) for (register int i=a;i<=b;i++)
#define per(i,a,b) for (register int i=a;i>=b;i--)
#define maxd 1000000007
typedef long long ll;
const int N=100000;
const double pi=acos(-1.0);
struct node{
	int x,y;
}point[200500];
bool operator<(const node &p,const node &q)
{
	return p.y>q.y;
}
bool cmp(node p,node q)
{
	return p.x<q.x;
}
int n,st1[200200],st2[200200];
ll ans=0;

int read()
{
	int x=0,f=1;char ch=getchar();
	while ((ch<'0') || (ch>'9')) {if (ch=='-') f=-1;ch=getchar();}
	while ((ch>='0') && (ch<='9')) {x=x*10+(ch-'0');ch=getchar();}
	return x*f;
}

void cdq(int l,int r)
{
	if (l==r) return;
	int mid=(l+r)>>1;
	cdq(l,mid);cdq(mid+1,r);
	sort(point+l,point+mid+1);
	sort(point+mid+1,point+r+1);
	int tp1=0,tp2=0,pos2=mid+1;
	rep(i,l,mid)
	{
		while ((pos2<=r) && (point[pos2].y>point[i].y))
		{
			while ((tp2) && (point[st2[tp2]].x>point[pos2].x)) tp2--;
			st2[++tp2]=pos2;pos2++;
		}
		while ((tp1) && (point[st1[tp1]].x<point[i].x)) tp1--;
		st1[++tp1]=i;
		if (tp1==1) ans+=tp2;
		else
		{
			int l=1,r=tp2,now=tp2+1,val=point[st1[tp1-1]].y;
			while (l<=r)
			{
				int mid=(l+r)>>1;
				if (point[st2[mid]].y>val) l=mid+1;
				else {r=mid-1;now=mid;}
			}
			ans+=(tp2-now+1);
		}
	}
} 	

int main()
{
	n=read();
	rep(i,1,n)
	{
		point[i].x=read();point[i].y=read();
	}
	sort(point+1,point+1+n,cmp);
	cdq(1,n);
	printf("%lld",ans);
	return 0;
}