区块链技术现状&前景

炒作周期

Gartner 在 2017 年发布的新兴技术炒作曲线，这张图是去年 8 月发布的，当时估计它们也没料到随后能有那么火，当时区块链在这个位置，其实是已经过了炒作的巅峰期，正在往低谷走的这个阶段，我觉得这张图其实特别精确，区块链在今年年初被炒到天上，但它的基础、它的技术并没有太大的变化，所以是支撑不了这个程度的炒作，一定会滑落下来，然后经历一段低谷，然后慢慢恢复。

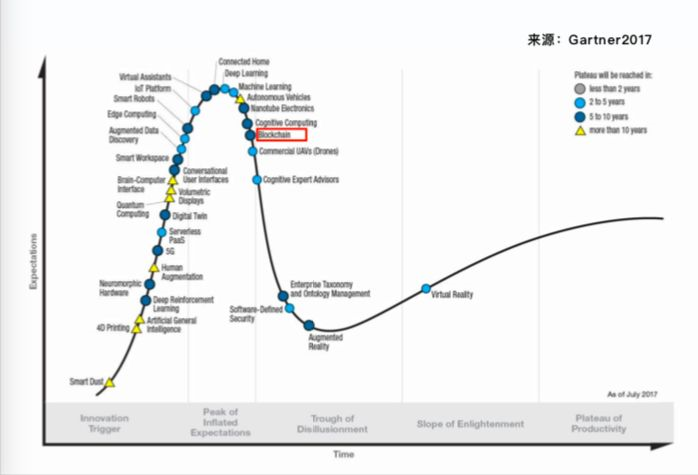
怎么去解读这个炒作曲线里的区块链呢？有一段被转载很多的话说的很精准：我们总是高估一项科技所带来的短期效益，却又低估它的长期影响。这就是阿玛拉定律。区块链就是这样的技术，被高估，被低估，就是不能正确的估计。

为什么不能正确的估计呢？我们认为这是因为区块链技术正处于它的极早期，未来的变数太多。这时候有人要说了，比特币是 2009 年发布的，以太坊是 2014 年发布的，两个现在都很流行，各自有数千万的用户，怎么能说是极早期呢？

这里举3个理由：

第一，在选择什么共识上我们还没有达成共识。我们发过一篇文章，现在有超过 30 种共识。POS、DPOS、拜占庭容错，看着都挺好，结果前一段时间有交易所被攻击了，大家又说，还是比特币的工作量证明好啊，所以，到底什么共识最好呢？这个事情本身到现在也没有达成共识。

第二，现在有些链宣称的 TPS 已经超过千万了，但是这样的链还没有正式上线，也不知道是不是真的。在过去，比特币以太坊最头疼的问题就是性能太差，经过各种攻关，现在大家宣称说解决了，口头说说很容易，但你这个链如果始终用的人不多，连以太坊的用户规模都达不到，那又有什么用呢？

第三，除了数字货币，还没有看到有说服力的应用。其实区块链的应用很多啊，我们的大会讲应用的就有很多，但是一个实践的时间不长，第二规模也不太大，人们也很难接触到，所以说服力没有那么强。这里我们还缺少一个区块链的 Killer App，是用来证明区块链能力的这样一种应用，现在还没看到。

远景与现状

对于区块链的前景，前几天陆奇宣布创办 Y 孵化器中国区，就说看好区块链的长远发展，所以这方面还是有的谈的。但这个事情一千个人有一千个看法，而且以空想居多，谁也说服不了谁，猜错了到将来被打脸也很难看，所以不谈远景，我们来谈谈现阶段区块链该怎么看。

首先区块链它不是银弹，不能解决一切问题，也不是锤子，不能看到一个问题就想着用区块链。

但是呢，你可以把区块链当做一般的工具，如果你想解决某个问题，用区块链确实适合，那为什么不用呢？

其次，我认为区块链是催化剂，它的意思是，区块链推动了以前很难推动的事情，比如说信息共享，你要用中心化的数据库来做个信息共享系统吧，你磨破了嘴皮子，也很难说动合作伙伴把数据放到你这里，但是如果用区块链的话，你说，数据就在你那里，他了解过区块链，说不定还炒过币，一下子就懂了，于是这个事情就成了。

最后，区块链可以是新平台。我们说智能手机之后的下一个平台在哪？可穿戴设备、IOT、VR，结果都没有火起来，然后以太坊搞的这个智能合约，还有基于这个智能合约的 DApp 火了，目前来看，支持 DApp 的底层公链还真有可能成为下一个平台。当然，我们说以前的苹果、谷歌是围墙花园，你的数据其实不属于你，到了区块链情况会不会不一样呢？我觉得不一定，还要拭目以待。

这是当前阶段的区块链，那如果说我是一个古典互联网人，怎么参与到区块链呢？我觉得比较现实的有两种姿势。

一种是信仰，说实话，当前阶段不炒币来做区块链特别是公链的人，那真的需要信仰啊，公链要技术上能投入实用，要把生态建立起来需要很长的过程，能耐住性子，经历创业九死一生，那不是信仰又是什么呢？这样的人值得尊敬，因为他们推动了真正的技术进步。

另一种是实用，深圳前不久开出了第一张基于区块链的发票，现在要想做联盟链相关的项目，其实真的机会很多，技术也相对的成熟，做做项目养家糊口很实际啊，这里区块链跟其它技术没什么两样。