LA 4329 Ping pong 树状数组

对于我这样一名脑残ACMer选手，这道题看了好久好久大概4天，终于知道怎样把它和“树状数组”联系到一块了。

树状数组是什么意思呢？用十个字归纳它：心里有数组，手中有前缀。

为什么要用树状数组？假设你要储存一段数字的前缀和，还要动态修改这些数字。怎么办？

通常的想法就是用数组a[]保存所有的数字，再用数组s[]保存每一位上的前缀和。

 for(int i=;i<=n;i++){

 　　s[i]=s[i-]+a[i];

 }

这样有一个弊端，就是当你动态修改a[]数组中的数字的时候，维护s[]数组的代价太高了，最坏可达O(N)，每修改一次都要O(N)的代价对于n=1000,000这样的的数据，显然修改十几次就要超时了。

那么这时候就可以用树状数组来存了，它的复杂度只有O(logN)。

也就是相当于把n二分的速度，非常快。

首先假设一个数组A[]和另一个保存其子串前缀和的数组C[]，形状如下图：

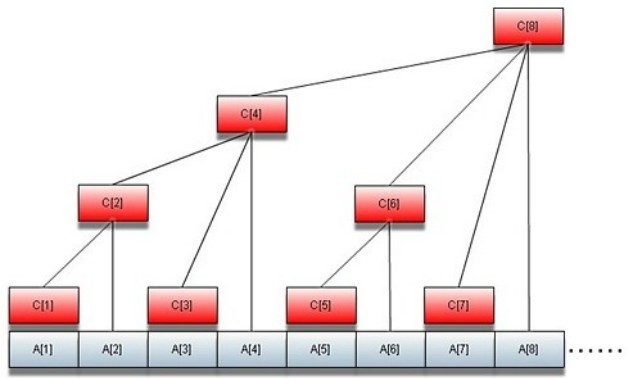
对于A[]数组，就是我所介绍的，心中的数组。

而C[]数组，就是手中的子串前缀和。

引入一个lowbit(x)的概念，lowbit(x)定义为x的二进制位最右边的1所对应的值，比如1表示1，10表示2，100表示4，这就是他们的值。lowbit只会为2^k(k>=0)。

令C[x]=A[x-lowbit(x)+1]+A[x-lowbit(x)+2]+...+A[x]，那么每个C[x]都会对应一部分它的lowbit(x)范围内的A[i]。

假如我要求x的前缀和，只要先取出C[x]，再取出C[x-lowbit(x)]也就是C[x]的左边界，令x=lowbit(x)也就是原来的C[x]的左边界的再左边一位，依次重复取C[x]，直到x=0。

比如拿x=7做一个示范，我要求x=7的前缀和，也就是A[1]+A[2]+...+A[7]，如下图：

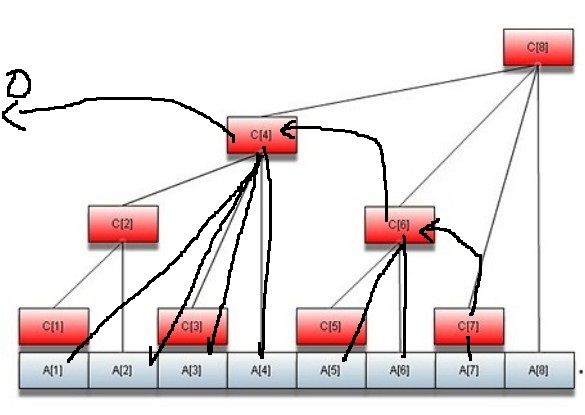
这样就求得了A[7]的前缀和。

实现：

 int lowbit(int x)
 {
     return x&(-x);
 }
 int sum(int x)
 {
     int ret=;
     for(;x;x-=lowbit(x))
         ret+=C[x];
     return ret;
 }

那当A[]某一位数据发生了变化，应该维护C[]的值，要注意A[]其实是你心里的数组，而C[]才是它的表现形式。

维护C[]就像是求有哪些C[]覆盖到了A[i]，对于A[3]来打个比方，如下图所示：

每次向右上方“爬”，x=3开始，修改C[x]，x加上自己的lowbit(x)，此时x=4，再修改C[4]，x加上自己的lowbit(x)，此时x=8，直到x超出了C数组的上界。

实现：

void updata(int x,int d)
{
    for(;x<=maxn;x+=lowbit(x))
        C[x]+=d;
}

现在把树形数组的概念运用到这道题里面来实践一下。

把运动员排成一排，对于其中任意一个位置i上的人来说，如果他作为裁判，则有这么两种可能：

1.左边的某人能力值低于他，右边高于他；

2.左边的某人能力值高于他，右边低于他。

记左边比他小的人数为l[i]，右边比他小的人数为r[i],

那么左边比他大的人数为i-1-l[i],右边比他大的人数为n-i-r[i]，

则i作为裁判就有l[i]*(n-i-r[i])+(i-1-l[i])*r[i];

求l[i]的方法呢，就是创一个hash数组，从a[1]扫到a[i-1]，对hash[a[k]]++，判断hash[]中a[i]的前缀和，也就是l[i]的值了；

前缀和就是用树状数组保存和维护。

r[i]类似，只不过是逆序读取a[i]构造hash表。

实现：

 #include <stdio.h>
 #include <string.h>
 const int maxn=;
 int C[maxn];
 int lowbit(int x)
 {
     return x&(-x);
 }
 int sum(int x)
 {
     int ret=;
     for(;x;x-=lowbit(x))
         ret+=C[x];
     return ret;
 }
 void updata(int x)
 {
     for(;x<=maxn;x+=lowbit(x))
         C[x]++;
 }
 int a[maxn],cc[maxn],dd[maxn];
 int main()
 {
     int i,t,n;
     long long ans;
     scanf("%d",&t);
     while(t--){
         scanf("%d",&n);
         for(i=;i<=n;i++) scanf("%d",&a[i]);
         memset(C,,sizeof(C));
         for(i=;i<=n;i++){
             cc[i]=sum(a[i]);
             updata(a[i]);
         }
         memset(C,,sizeof(C));
         for(i=n;i;i--){
             dd[i]=sum(a[i]);
             updata(a[i]);
         }
         ans=;
         for(i=;i<=n;i++)
             ans+=1LL*cc[i]*(n-i-dd[i])+1LL*(i--cc[i])*dd[i];
         printf("%lld\n",ans);
     }
     return ;
 }