数学建模python matlab 编程(喷泉模拟)
在无风情况下的喷泉模拟
我的python代码
import numpy as np
import random
import matplotlib
matplotlib.rcParams['font.sans-serif']=[u'simHei']
matplotlib.rcParams['axes.unicode_minus']=False
import matplotlib.pyplot as plt tt = np.linspace(0,4,1000)
#y = -tt**2+4*tt
#plt.plot(tt,y,linestyle='--') # 没有风
vy0=10
g=10
vx0=5
x=[]
y=[]
x0=0
y0=0
dt = 4/1000
x.append(x0)
y.append(y0)
for t in tt:
y0 += vy0*dt
x0 += vx0*dt
vy0 -= g*dt
x.append(x0)
y.append(y0)
if y0<0:
break
plt.plot(x,y,linestyle='--')
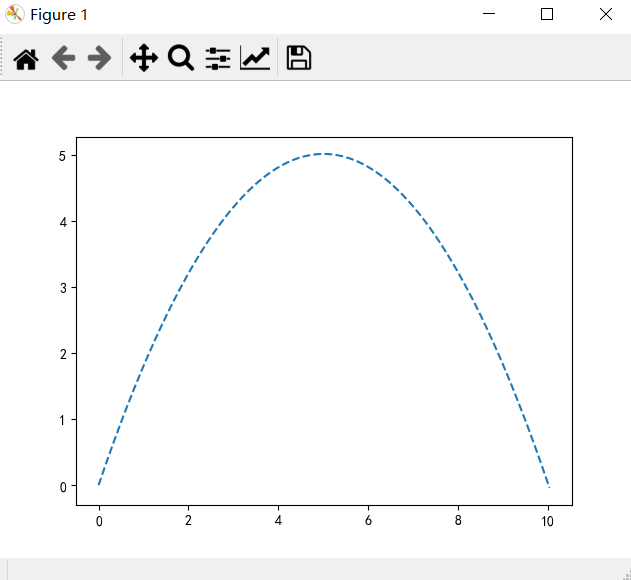
在右边风情况下的喷泉模拟
我的python代码
# 有向右的风
vy0=10
g=10
vx0=5
a = 1.5
x=[]
y=[]
x0=0
y0=0
dt = 4/1000
x.append(x0)
y.append(y0)
for t in tt:
y0 += vy0*dt
x0 += vx0*dt
vy0 -= g*dt
vx0 -= a*dt
x.append(x0)
y.append(y0)
if y0<0:
break
plt.plot(x,y)
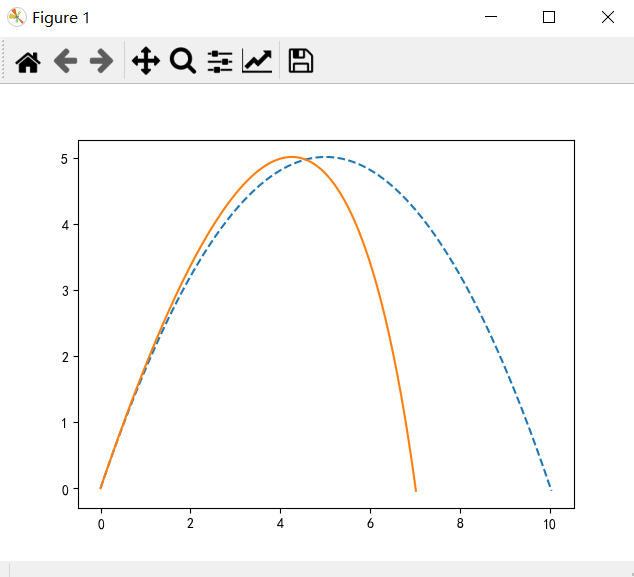
在左边风情况下的喷泉模拟
我的python代码
# 有向左的风
vy0=10
g=10
vx0=5
a = -1.5
x=[]
y=[]
x0=0
y0=0
dt = 4/1000
x.append(x0)
y.append(y0)
for t in tt:
y0 += vy0*dt
x0 += vx0*dt
vy0 -= g*dt
vx0 -= a*dt
x.append(x0)
y.append(y0)
if y0<0:
break
plt.plot(x,y)
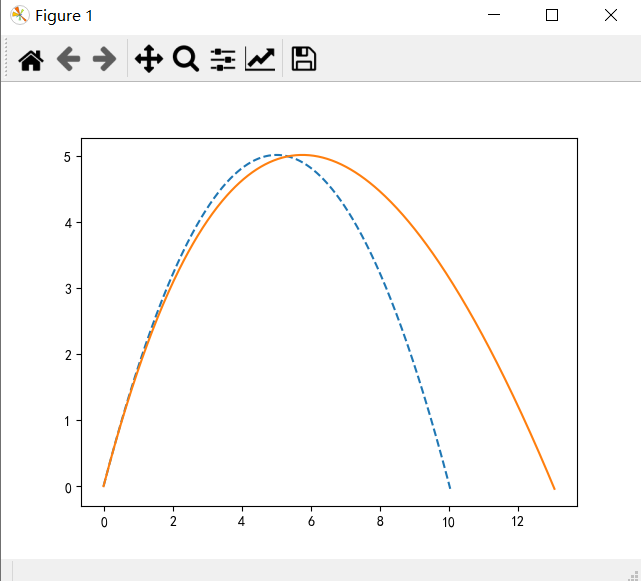
所有代码
# -*- coding: utf-8 -*- import numpy as np
import random
import matplotlib
matplotlib.rcParams['font.sans-serif']=[u'simHei']
matplotlib.rcParams['axes.unicode_minus']=False
import matplotlib.pyplot as plt tt = np.linspace(0,4,1000)
#y = -tt**2+4*tt
#plt.plot(tt,y,linestyle='--') # 没有风
vy0=10
g=10
vx0=5
x=[]
y=[]
x0=0
y0=0
dt = 4/1000
x.append(x0)
y.append(y0)
for t in tt:
y0 += vy0*dt
x0 += vx0*dt
vy0 -= g*dt
x.append(x0)
y.append(y0)
if y0<0:
break
plt.plot(x,y,linestyle='--') # 有向右的风
vy0=10
g=10
vx0=5
a = 1.5
x=[]
y=[]
x0=0
y0=0
dt = 4/1000
x.append(x0)
y.append(y0)
for t in tt:
y0 += vy0*dt
x0 += vx0*dt
vy0 -= g*dt
vx0 -= a*dt
x.append(x0)
y.append(y0)
if y0<0:
break
plt.plot(x,y) # 有向左的风
vy0=10
g=10
vx0=5
a = -1.5
x=[]
y=[]
x0=0
y0=0
dt = 4/1000
x.append(x0)
y.append(y0)
for t in tt:
y0 += vy0*dt
x0 += vx0*dt
vy0 -= g*dt
vx0 -= a*dt
x.append(x0)
y.append(y0)
if y0<0:
break
plt.plot(x,y)

喷泉散落在地上模拟
import numpy as np
import random
import matplotlib
matplotlib.rcParams['font.sans-serif']=[u'simHei']
matplotlib.rcParams['axes.unicode_minus']=False
import matplotlib.pyplot as plt
from scipy.stats import norm
a1_list = random.uniform(0,0.5) # 生成一组正太分布的加速度,均值是0,方差是0.5
a1_list = norm.rvs(a1_list, size=1000)
a2_list = random.uniform(0,0.5)
a2_list = norm.rvs(a2_list, size=1000)
X0=[]
X1=[]
# 对每一组加速度
for i in range(1000):
vy0=10
g=10
vx0=5
vx1=5
a1 = a1_list[i]
a2 = a2_list[i]
x0=0
x1=0
y0=0
dt = 4/1000
for t in tt:
y0 += vy0*dt
x0 += vx0*dt
x1 += vx1*dt vy0 -= g*dt
vx0 -= a1*dt
vx1 -= a2*dt if y0<0:
break
X0.append(x0)
X1.append(x1) plt.scatter(X0,X1)
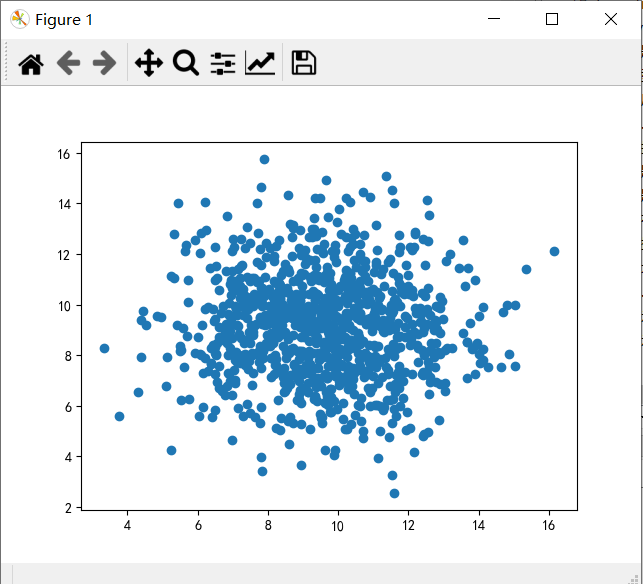
炫酷喷泉三维图
from mpl_toolkits.mplot3d import axes3d
from scipy.stats import norm
a1_list = random.uniform(0,0.2) # 生成一组正太分布的加速度,均值是0,方差是0.5
a1_list = norm.rvs(a1_list, size=100)
a2_list = random.uniform(0,0.2)
a2_list = norm.rvs(a2_list, size=100)
X0=[]
X1=[]
# 对每一组
ax=plt.subplot(111,projection='3d')
for i in range(100):
vy0=10
g=10
vx0=5
vx1=5
a1 = a1_list[i]
a2 = a2_list[i]
xx0=[]
xx1=[]
y=[]
x0=0
x1=0
y0=0
dt = 4/1000
for t in tt:
y0 += vy0*dt
x0 += vx0*dt
x1 += vx1*dt
vy0 -= g*dt
vx0 -= a1*dt
vx1 -= a2*dt
xx0.append(x0)
xx1.append(x1)
y.append(y0)
if y0<0:
break
# X0.append(x0)
# X1.append(x1) ax.plot(xx0,xx1,y,'--') plt.show()
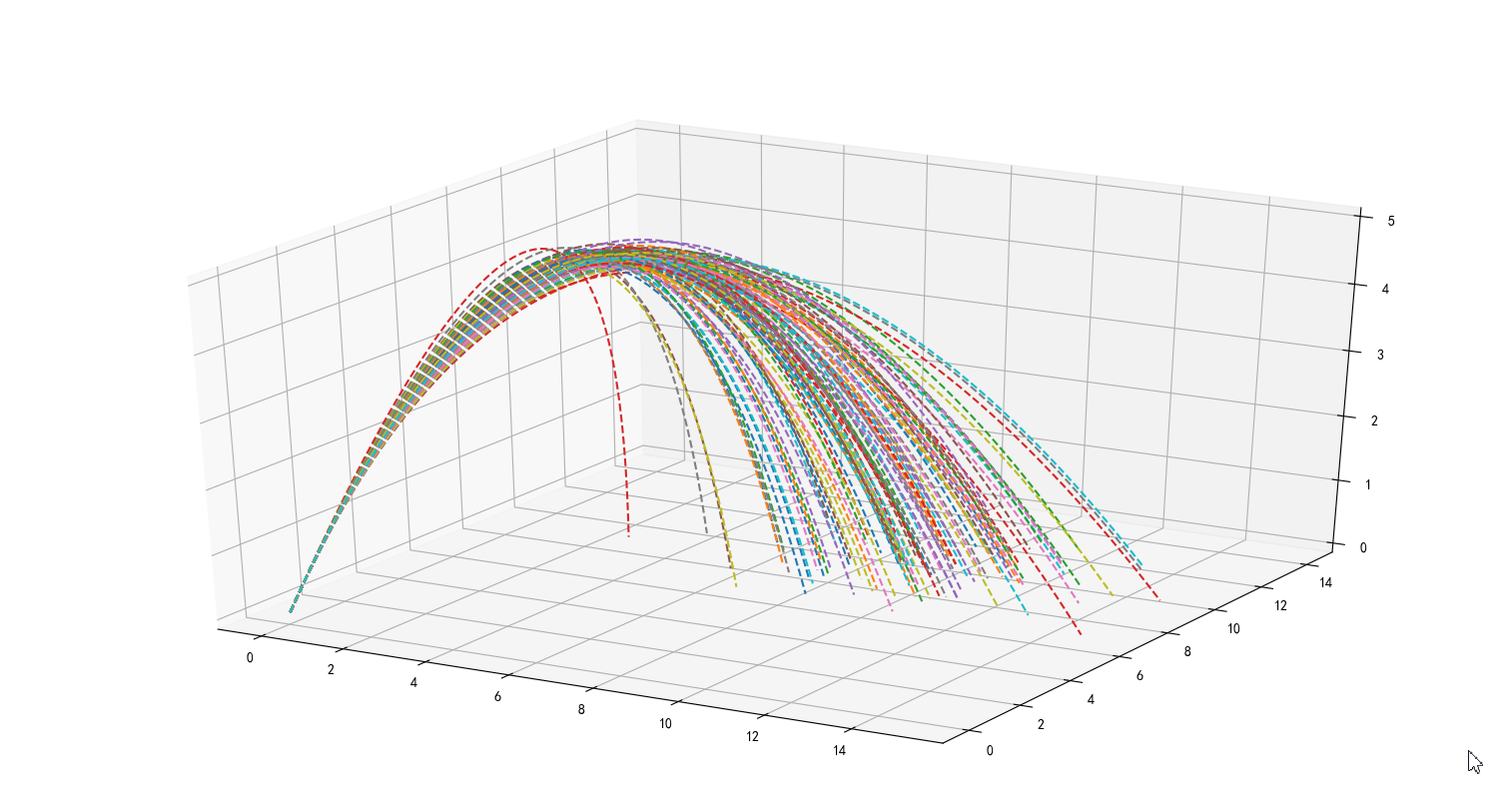
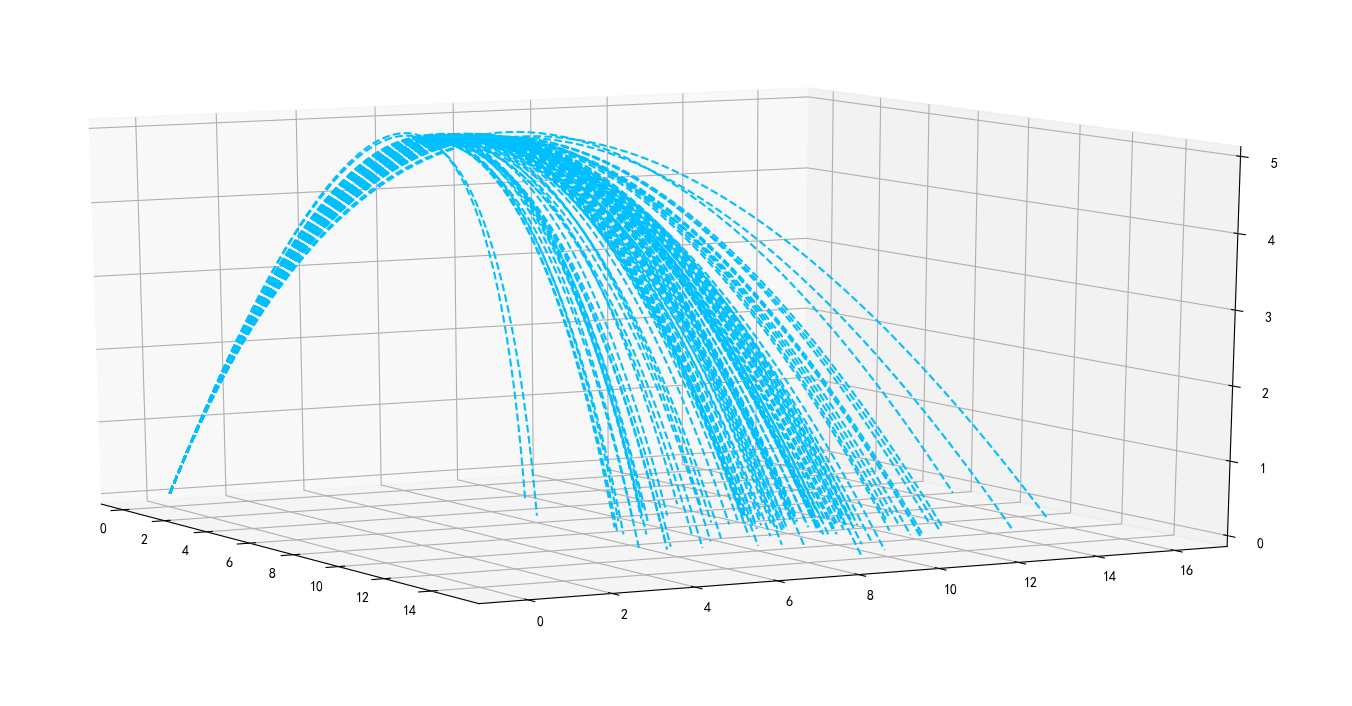
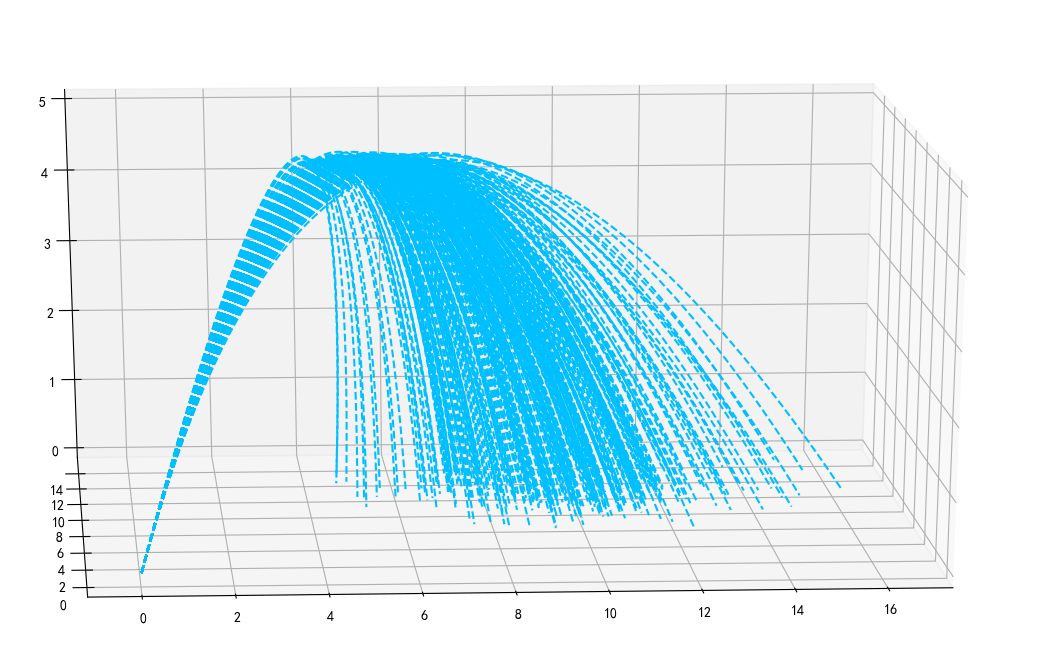
数学建模python matlab 编程(喷泉模拟)的更多相关文章
- 数学建模python matlab 编程(疾病传播模型)
例12:一只游船上有800(1000)人,一名游客不慎患传染病,12(10)小时后有3人发病,由于船上不能及时隔离,问经过60(30)小时,72小时,患此病的人数.(与人口模型和Logistic模型类 ...
- 数学建模python matlab 编程(指派问题)
指派授课问题 现有A.B.C.D四门课程,需由甲.乙.丙.丁四人讲授,并且规定: 每人只讲且必须讲1门课:每门课必须且只需1人讲. 四人分别讲每门课的费用示于表中: 课 费用 人 A B C D 甲 ...
- 数学建模python matlab 编程(随机游走问题)
1 (1). 随机游走问题.在-10到10的一维线段上,质点以1/5的概率用左运动1单位,以2/5的概率停止不动,以2/5的概率向右运动2单位,且碰到-10时向右运动3单位,碰到10时向左运动4单位. ...
- 数学建模python matlab 编程(椭圆声学原理画图证明,解析几何)
证明,在椭圆形的音乐厅内,从一个椭圆的一个焦点发出声音,则另一个焦点听到的声音是最大的. 分析:证明,从椭圆的一个焦点任意发射的直线经过反射后,并经过另一个焦点. 画图,过一个焦 ...
- 在数学建模中学MATLAB
为期三周的数学建模国赛培训昨天正式结束了,还是有一定的收获的,尤其是在MATLAB的使用上. 1. 一些MATLAB的基础性东西: 元胞数组的使用:http://blog.csdn.net/z1137 ...
- 【数学建模】MatLab 数据读写方法汇总
1.读入 txt 文件数据. load xxx.txt A=load(‘xxx.txt’) A=dlmread(‘xxx.txt’) A=importdata(‘xxx.txt’) 例:将身高体重的 ...
- 【数学建模】MATLAB语法
一.向量.矩阵的表示和使用 format long %小数很多format short %默认4位小数format rat %显示最近的分数format short e %指数格式的数 尾数多少 e ...
- 【数学建模】MATLAB学习笔记——函数式文件
MATLAB学习笔记——函数式文件 引入函数式文件 说明: 函数式文件主要用于解决计算中的参数传递和函数调用的问题. 函数式的标志是它的第一行为function语句. 函数式文件可以有返回值,也可以没 ...
- python 并发编程 多进程 模拟抢票
抢票是并发执行 多个进程可以访问同一个文件 多个进程共享同一文件,我们可以把文件当数据库,用多个进程模拟多个人执行抢票任务 db.txt {"count": 1} 并发运行,效率高 ...
随机推荐
- RedHat Enterprise Linux 5 配置Samba服务器
1.修改samba的配置文件 # gedit /etc/samba/smb.conf 在/etc/samba/smb.conf配置文件中找到Share Definitions模块添加以下代码: [ro ...
- Web服务器主动推送技术
HTTP协议遵循经典的客户端-服务器模型,客户端发送一个请求,然后等待服务器端的响应,服务器端只能在接收到客户端的请求之后进行响应,不能主动的发送数据到客户端. 客户端想要在不刷新页面的情况下实时获取 ...
- 如何python循环中删除字典元素
//下面这行就是在循环中遍历删除字典元素的方法! for i in list(dictheme2.keys()): if dictheme2[i]<self.countFortheme: dic ...
- .Net优秀应用界面大PK!DevExpress年度大赛,群雄逐鹿花落谁家
DevExpress 优秀界面图片火热征集中! 只要您晒出来,慧都就为您颁奖! 角逐前三,百度AI音箱.小米行李箱等惊喜大礼等您Pick! 活动时间:12月1日-12月31日 立即参与 活动详情 活动 ...
- BZOJ 2127 / Luogu P1646 [国家集训队]happiness (最小割)
题面 BZOJ传送门 Luogu传送门 分析 这道题又出现了二元关系,于是我们只需要解方程确定怎么连边就行了 假设跟SSS分在一块是选文科,跟TTT分在一块是选理科,先加上所有的收益,再来考虑如何让需 ...
- java-十五周作业
题目1:编写一个应用程序,输入用户名和密码,访问test数据库中t_login表(字段包括id.username.password),验证登录是否成功. 题目2:在上一题基础上,当登录成功后,将t_u ...
- 【基本算法入门-字符串哈希(Hash)】-C++
字符串哈希入门 说得通俗一点,字符串哈希实质上就是把每个不同的字符串转成不同的整数. 为什么会有这样的需要呢?很明显,存储一个超长的字符串和存储一个超大但是能存的下的整数,后者所占的空间会少的多,但主 ...
- 百度ueditor中复制word图文时图片转存任然保持灰色不可用
官网地址http://ueditor.baidu.com Git 地址 https://github.com/fex-team/ueditor 参考博客地址 http://blog.ncmem.com ...
- 线段树QWQ
一直没碰过线段树,个人认为好长好难,不过这几天做题遇到了裸的线段树的题,TAT. 线段树我理解就是把二叉树的左右节点现在分别看成是两个区间. 那么现在这两个区间的端点怎么存放?怎么能够把这个区间里的数 ...
- JavaWeb_(Spring框架)Spring与JDBC
一.用Spring中的JdbcTemplate操作数据库 在MySQL中准备一个user表,表中增加一条假数据 用Spring中的JdbcTemplate操作数据库,在JdbcTemplate中实现增 ...
