P2699 【数学1】小浩的幂次运算

原题链接 https://www.luogu.org/problemnew/show/P2699

P2699 【数学1】小浩的幂次运算

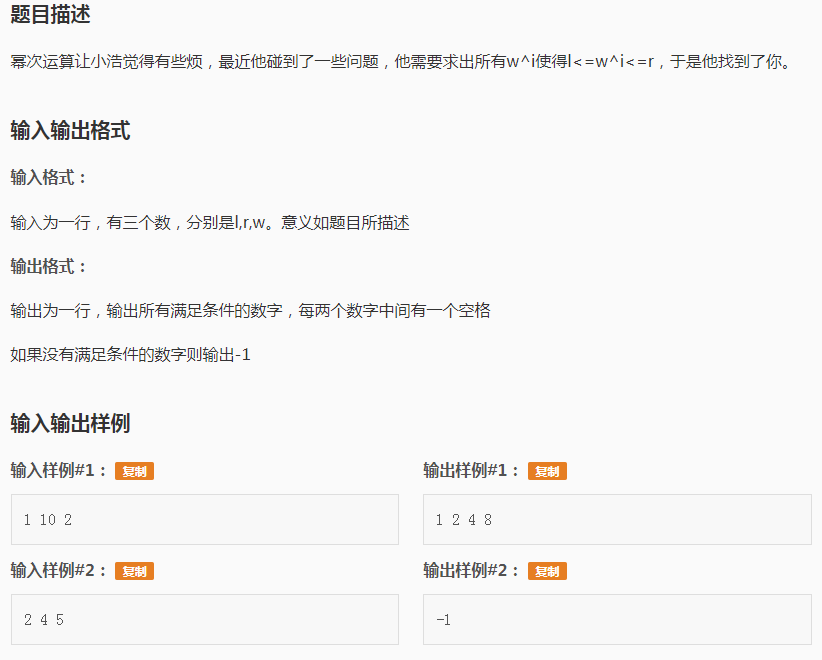
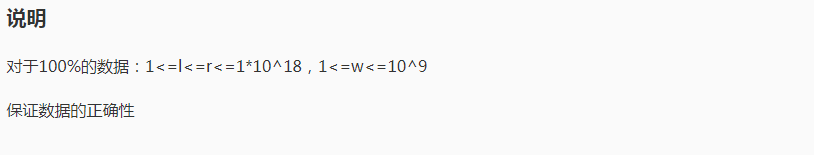
首先第一眼看这个题就知道要暴力枚举w^i 看是否在区间[l，r]里内就好啦，注意w=1的情况，如果不特判一下它就会一直死循环从而TLE；

我是先用一次while（w^i<l）除去前面不在区间内的i，然后再来一次while（w^i<=r）输出所有在区间内的i；

还有就是#7的数据乘出来会爆long long，用unsigned long long 也水不过去，所以我这里用的__int128，也是现学现卖啊qwq：

关于__int128的几个需要注意的点：

1.__int128前面有两个下划线；

2.讲道理的话，编译器的gcc是不支持__int128这种数据类型的，比如在codeblocks 16.01/Dev C++是无法编译的，但是提交到大部分OJ上是可以编译且能用的。C/C++标准。IO是不认识__int128这种数据类型的，因此要自己实现IO，其他的运算，与int没有什么不同；

3.__int128不能用 scanf/printf 或 cin/cout 来输入输出的，所以你需要自己写一套输入输出；

AC代码如下：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
__int128 l,r,k;
__int128 read()                   //自定义__int128的输入（其实就是快读）
{
    char ch=getchar();
    __int128 a=;
    while(ch<''||ch>'')
    {
        ch=getchar();
    }
    while(ch>=''&&ch<='')
    {
        a=(a<<)+(a<<)+(ch^'');
        ch=getchar();
    }
    return a;
}
void print(const __int128 x)      //自定义__int128的输出，因为__int128类型的数太大了，所以我们要以字符的形式从高位到低位一个一个输出，具体做法就是递归
{
    if(x<) putchar('-');         //是负数先输出负号‘-’
    if(x>) print(x/);          //如果x是多位数，我们除以10去找它的高位
    putchar(x%+'');            //最后再输出最后一位，注意后面加上‘0’
    return ;                      //返回
}
int main()
{
    l=read();
    r=read();
    k=read();
    if(k==)
    {
        if(l<=&&r>=) cout<<;
        else cout<<-;
        return ;
    }
    __int128 m=,flag=;
    while(m<l)                    //除去前面在区间外的点
    {
        m*=k;                     //这里一次一次乘过去比每次求k^i要快
    }
    while(m<=r)                   //输出再区间内的点
    {
        flag=;                   //说明有解，标记一下
        print(m);                 //输出__int128类型的m
        putchar(' ');
        m*=k;
    }
    if(flag) cout<<-;            //判断无解
    return ;
} 

这个题解应该不是纯正的正解（毕竟我用了__int128），仅作为参考qwq。