hdu 5761 Rower Bo 微分方程

Rower Bo

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 131072/131072 K (Java/Others)
Total Submission(s): 641    Accepted Submission(s): 199
Special Judge

Problem Description

There is a river on the Cartesian coordinate system,the river is flowing along the x-axis direction.

Rower Bo is placed at (0,a) at first.He wants to get to origin (0,0) by boat.Boat speed relative to water is v1,and the speed of the water flow is v2.He will adjust the direction of v1 to origin all the time.

Your task is to calculate how much time he will use to get to origin.Your answer should be rounded to four decimal places.

If he can't arrive origin anyway,print"Infinity"(without quotation marks).

 

Input

There are several test cases. (no more than 1000)

For each test case,there is only one line containing three integers a,v1,v2.

0≤a≤100, 0≤v1,v2,≤100, a,v1,v2 are integers

 

Output

For each test case,print a string or a real number.

If the absolute error between your answer and the standard answer is no more than 10−4, your solution will be accepted.

 

Sample Input

2 3 3
2 4 3

 

Sample Output

Infinity
1.1428571429

 

Source

2016 Multi-University Training Contest 3

 

Recommend

wange2014   |   We have carefully selected several similar problems for you:       

 题意：一艘船在y轴非负轴上，一个岛在原点，任何时刻船的速度方向都指向岛，船的速度为v1，河流的速度为v2，且是向x轴正方向流，问船到达岛的最短时间；

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <cmath>
#include <vector>
#include <queue>
#include <stack>
#include <map>
#include <algorithm>
#include <set>
using namespace std;
typedef long long ll;
typedef unsigned long long Ull;
#define MM(a,b) memset(a,b,sizeof(a));
const double eps = 1e-10;
const int  inf =0x7f7f7f7f;
const double pi=acos(-1);
const int mod=1e9+7;
const int maxn=100000+10;
ll f_2[1000+10];

#define FOR(i,n) for(int i=1;i<=n;i++)
#define SC scanf
#define PF printf

int main()
{
    int a,v1,v2;
    while(~SC("%d%d%d",&a,&v1,&v2)){
        if(a!=0&&v1<=v2) PF("Infinity\n");
        else if(!a) PF("0\n");
        else  PF("%.9f\n",v1*a/((double)(v1*v1-v2*v2)));
    }
    return 0;
}

　　

1010 Rower Bo

首先这个题微分方程强解显然是可以的，但是可以发现如果设参比较巧妙就能得到很方便的做法。

先分解v_1v​1​​，

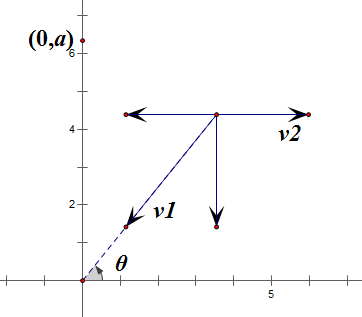
设船到原点的距离是rr，容易列出方程

\frac{ dr}{ dt}=v_2\cos \theta-v_1​dt​​dr​​=v​2​​cosθ−v​1​​

\frac{ dx}{ dt}=v_2-v_1\cos \theta​dt​​dx​​=v​2​​−v​1​​cosθ

上下界都是清晰的，定积分一下：

0-a=v_2\int_0^T\cos\theta{ d}t-v_1T0−a=v​2​​∫​0​T​​cosθdt−v​1​​T

0-0=v_2T-v_1\int_0^T\cos\theta{ d}t0−0=v​2​​T−v​1​​∫​0​T​​cosθdt

直接把第一个式子代到第二个里面

v_2T=\frac{v_1}{v_2}(-a+v_1T)v​2​​T=​v​2​​​​v​1​​​​(−a+v​1​​T)

T=\frac{v_1a}{{v_1}^2-{v_2}^2}T=​v​1​​​2​​−v​2​​​2​​​​v​1​​a​​

这样就很Simple地解完了，到达不了的情况就是v_1< v_2v​1​​<v​2​​（或者a>0a>0且v_1=v_2v​1​​=v​2​​）。

题解链接：