Dijkstra算法和Floyd算法

一、简介

迪杰斯特拉(Dijkstra)算法和弗洛伊德(Flyod)算法均是用于求解有向图或无向图从一点到另外一个点最短路径。

二、Dijkstra

迪杰斯特拉算法也是图论中的明星算法，主要是其采用的动态规划思想，使其在数据结构、算法、离散数学乃至运筹学中都扮演重要的角色。以下图为例：

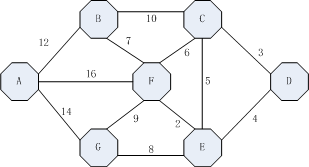
以A为起点，首先走一步，共有三条边，分别如下：

AB(12),AF(16),AG(14)其中最短的是节点B，将AB(12)放入辅助向量。

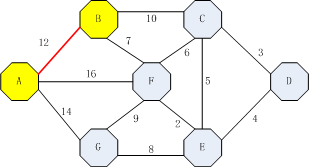
接着，各节点均继续向下走，此时可以找出4条边。

ABC(22),ABF(19),AF(16),AG(14),同样找出最小值放入向量中。{AB(12)，AG(14)}

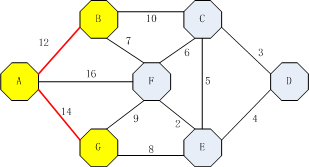
此后步骤完全相同

ABC(22),ABF(19),AF(16),AGF(23),AGE(22)，选中AF(16)。

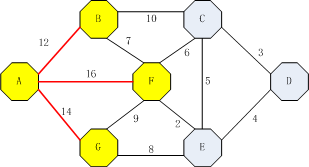
同样，接下来的步骤有：ABC(22),AFC(22),AFE(18),AGE(22)，选中AFE(18);

ABC(22),AFC(22),AFEC(23),AFED(22)，这种情况随便选取一个最小值，以ABC(22)为例；

ABCD(25),AFED(22)选中后者，至此，已经完全找到A和所有节点之间的最短路径及最短路径的长度。

最短路径向量为{AB(12)，AG(14)，AF(16)，AFE(18)，ABC(22)，AFED(22)}

三、Floyd

弗洛伊德是另外一种求最短路径的方式，与迪杰斯特拉算法不同，弗洛伊德偏重于多源最短路径的求解，即能迪杰斯特拉能够求一个节点到其余所有节点的最短路径，但是弗洛伊德能够求出任意两个节点的最短路径，当然迪杰斯特拉重复N次也能达到目标。两种方式的时间复杂度均为O(n^3)，但弗洛伊德形式上会更简易一些。

以下面的有向有权图为例：

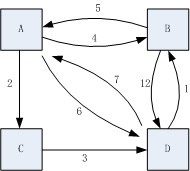
老版visio不知道为啥这么糊？

首先写出图的邻接矩阵Adj

	A	B	C	D
A	0	4	2	6
B	5	0	∞	12
C	∞	∞	0	3
D	7	1	∞	0

若想缩短两点间的距离，仅有一种方式，那就是通过第三节点绕行，如果我们假设仅能通过A点绕行，那么仅需判断是否现有的距离Adj[i][j]小于Adj[i][1]+Adj[1][j]的距离，如果有更短的选择，那么进行更新就好了。首先第一行和第一列肯定不会更新，然后对角线也不必更新。【其实通过观察可以知道，第三行也不会进更新，因为C根本无法绕到A】

0	4	2	6
5	0	7	11
∞	∞	0	3
7	1	9	0

接下来，开放绕行节点2，那么就相当于可以经过节点1和2进行绕行。更新条件是Adj[i][j]>Adj[i][2]+Adj[2][j]，除去第2行，第2列和对角线不需要进行判断。可以到D到C通过B-A会比仅通过A更短。

0	4	2	6
5	0	7	11
∞	∞	0	3
6	1	8	0

然后开放节点3.

0	4	2	5
5	0	7	10
∞	∞	0	3
6	1	8	0

最后开放节点4.

0	4	2	5
5	0	7	10
9	4	0	3
6	1	8	0

最短路径不适用于负权回路，或负权环，因为每次绕行都会减小最短路径，因此负权回路或者说负权环不存在最短路径。