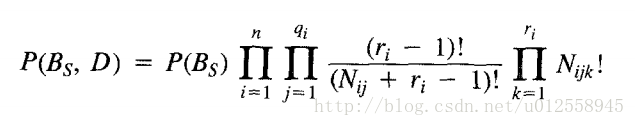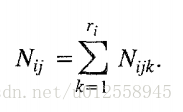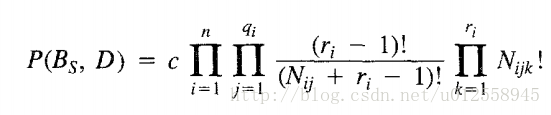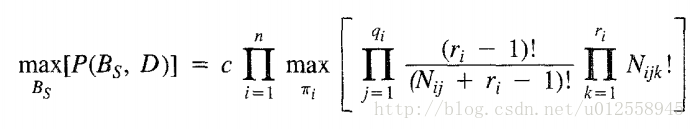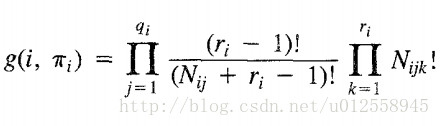基于搜索的贝叶斯网络结构学习算法-K2
一 算法简介
基于搜索的贝叶斯网络结构学习算法核心主要包含两块:一是确定评分函数,用以评价网络结构的好坏。二是确定搜索策略以找到最好的结果。
二 评分函数
对网络结构的学习其实可以归结为求给定数据D下,具有最大后验概率的网络结构Bs,即求Bs使P(Bs| D)最大。
而P(Bs | D) = P(Bs , D) / P(D),分母P(D)与Bs无关,所以最终的目标是求使P(Bs , D)最大的Bs,通过一系列推导(具体推导过程请看最上方链接的paper),可以得到:
其中P(Bs)是关于关于Bs的先验概率,也就是在不给定数据的情况下,我们给每种结构设定的概率。在后面,我们可以假设每种结构的概率服从均匀分布,即概率都是相同的常数c。
令Z是一个包含n个离散随机变量的集合,每个变量Xi有ri种可能的取值(Vi1,Vi2.....Viri)。令D一个数据库,包含m个case,每个case就是对所有Z中随机变量的实例化。用Bs表示一个正好包含Z中随机变量的信念网络。变量Xi在Bs中的父节点表示为πi。Wij表示πi的第j种实例化。πi共有qi种实例化。比如变量Xi有2个父变量,第一个父变量有2种取值,第二个父变量有3种取值,那么qi最多为2*3=6。Nijk表示数据D中Xi取值为Vik并且πi被实例化为Wij。同时:
第一个连乘符号通过i遍历每个随机变量Xi,n为随机变量的个数。
第二个连乘符号通过j遍历当前变量Xi的所有父变量实例,qi表示变量Xi父变量实例的种类数。。
最后一个连乘符号变量遍历当前变量Xi的所有可能取值,ri为可能取值的个数。
用常数代替P(Bs)后:
我们的目标是寻找Bs使后验概率最大:
当找到一个最好的网络结构,把该结构下的Nijk数据带入上式可以得到最大值。从上式可以看出,我们只要最大化每个变量的局部最大,就能得到整体最大。我们将每个变量的部分提出来作为新的评分函数:
三 搜索策略
因此,我们只要对每个变量求出使评分函数最大的父变量集。K2算法使用贪心搜索去获取最大值。首先假设随机变量是有顺序的,如果Xi在Xj之前,那么不能存在从Xj到Xi的边。同时假设每个变量最多的父变量个数为u。每次挑选使评分函数最大的父变量放入集合,当无法使评分函数增大时,停止循环,具体算法如下,其中Pred(Xi)表示顺序在Xi之前的变量:
四 算法拓展
其实我们可以计算log g(i, πi),而不是直接计算g(i, πi)。因为通过log函数可以将乘法运算转变为加法运算。
还有一种算法叫做K2R(K2 Reverse),它从一个全连接的信念网络开始,不断应用贪心算法从结构中移除边。我们可以用K2和K2R分别学习两个结构并从中挑选后验概率更大的结构。也可以在执行K2算法时,初始化不同的节点顺序,并挑选输出的网络结构中较好的那个。
基于搜索的贝叶斯网络结构学习算法-K2的更多相关文章
- 贝叶斯深度学习(bayesian deep learning)
本文简单介绍什么是贝叶斯深度学习(bayesian deep learning),贝叶斯深度学习如何用来预测,贝叶斯深度学习和深度学习有什么区别.对于贝叶斯深度学习如何训练,本文只能大致给个介绍. ...
- ZhuSuan 是建立在Tensorflow上的贝叶斯深层学习的 python 库
ZhuSuan 是建立在Tensorflow上的贝叶斯深层学习的 python 库. 与现有的主要针对监督任务设计的深度学习库不同,ZhuSuan 的特点是深入到贝叶斯推理中,从而支持各种生成模式:传 ...
- 基于MapReduce的贝叶斯网络算法研究参考文献
原文链接(系列):http://blog.csdn.net/XuanZuoNuo/article/details/10472219 论文: 加速贝叶斯网络:Accelerating Bayesian ...
- 机器学习集成算法--- 朴素贝叶斯,k-近邻算法,决策树,支持向量机(SVM),Logistic回归
朴素贝叶斯: 是使用概率论来分类的算法.其中朴素:各特征条件独立:贝叶斯:根据贝叶斯定理.这里,只要分别估计出,特征 Χi 在每一类的条件概率就可以了.类别 y 的先验概率可以通过训练集算出 k-近邻 ...
- 3.朴素贝叶斯和KNN算法的推导和python实现
前面一个博客我们用Scikit-Learn实现了中文文本分类的全过程,这篇博客,着重分析项目最核心的部分分类算法:朴素贝叶斯算法以及KNN算法的基本原理和简单python实现. 3.1 贝叶斯公式的推 ...
- BPR贝叶斯个性化排序算法
全序关系:集合中的任两个元素之间都可以比较的关系.
- 基于贝叶斯网(Bayes Netword)图模型的应用实践初探
1. 贝叶斯网理论部分 笔者在另一篇文章中对贝叶斯网的理论部分进行了总结,在本文中,我们重点关注其在具体场景里的应用. 2. 从概率预测问题说起 0x1:条件概率预测模型之困 我们知道,朴素贝叶斯分类 ...
- NeurIPS 2018 中的贝叶斯研究
NeurIPS 2018 中的贝叶斯研究 WBLUE 2018年12月21日 雷锋网 AI 科技评论按:神经信息处理系统大会(NeurIPS)是人工智能领域最知名的学术会议之一,NeurIPS 2 ...
- R语言︱贝叶斯网络语言实现及与朴素贝叶斯区别(笔记)
每每以为攀得众山小,可.每每又切实来到起点,大牛们,缓缓脚步来俺笔记葩分享一下吧,please~ --------------------------- 一.贝叶斯网络与朴素贝叶斯的区别 朴素贝叶斯的 ...
随机推荐
- /dev/mem同步写不能使用msync的MS_SYNC选项探究
问题 做了个测试板子的程序,里面有一项写铁电的功能,要求写入之后立即断电,重启后校验数据准确性:铁电设计是通过内存地址直接映射的,于是,使用mmap直接映射了/dev/mem文件,自然地写入之后使用m ...
- macbook配置flutter环境变量
打开命令窗口,如果没有文件的,可以手动创建文件 code ~/.bash_profile 打开的文件内容如下,如果新增的空文件,肯定是空白的 如果将flutter存放到了应用中,可以如下操作,如果不是 ...
- 快速安装python3
使用 rpm 包进行安装 先来介绍一下 IUS 这个社区,名字的全写是[Inline with Upstream Stable]取首字母,它主要是一个提供新版本RPM包的社区.具体使用可以查看官方文档 ...
- ? 原创: 铲子哥 搜狗测试 今天 shell编程的时候,往往不会把所有功能都写在一个脚本中,这样不太好维护,需要多个脚本文件协同工作。那么问题来了,在一个脚本中怎么调用其他的脚本呢?有三种方式,分别是fork、source和exec。 1. fork 即通过sh 脚本名进行执行脚本的方式。下面通过一个简单的例子来讲解下它的特性。 创建father.sh,内容如下: #!/bin/bas
? 原创: 铲子哥 搜狗测试 今天 shell编程的时候,往往不会把所有功能都写在一个脚本中,这样不太好维护,需要多个脚本文件协同工作.那么问题来了,在一个脚本中怎么调用其他的脚本呢?有三种方式,分别 ...
- python笔记7 logging模块 hashlib模块 异常处理 datetime模块 shutil模块 xml模块(了解)
logging模块 日志就是记录一些信息,方便查询或者辅助开发 记录文件,显示屏幕 低配日志, 只能写入文件或者屏幕输出 屏幕输出 import logging logging.debug('调试模式 ...
- 自定义控件之canvas变换和裁剪
1.平移 //构造两个画笔,一个红色,一个绿色 Paint paint_green = generatePaint(Color.GREEN, Paint.Style.STROKE, 3); Paint ...
- spring bean容器加载后执行初始化处理@PostConstruct
先说业务场景,我在系统启动后想要维护一个List常驻内存,因为我可能经常需要查询它,但它很少更新,而且数据量不大,明显符合缓存的特质,但我又不像引入第三方缓存.现在的问题是,该List的内容是从数据库 ...
- 【用户体验】Google关闭标签的体验
https://www.uisdc.com/hunter/0221334485.html 在优设-细节猎人里有不少好案例.
- centos6.8yum 安装mysql
1:查看是否已有mysql版本 rpm -qa | grep mysql 删除mysql 账号和用户组 删除/etc/my.cnf 2:有的话就删除 rpm -e mysql-...... 或者 co ...
- python迭代器、生成器、装饰器之装饰器
装饰器...... 定义:本质是函数,为其他函数添加附加功能 原则: 1.不能修改被装饰的函数的源代码 2.不能修改被装饰函数的调用方式 仔细观察下面代码,看看有什么发现. 内嵌函数+高阶函数+闭包= ...